2023年中考数学真题分类汇编(全国版):三角形(4)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,B为上一点,OB⊥AC于D. 若AC=m,BD=150m,则的长为( )
 A、m B、m C、m D、m2. 如图,该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分.若该几何体上、下两个圆的半径分别为1和2,原大圆锥高的剩余部分为 , 则其侧面展开图的面积为( )
A、m B、m C、m D、m2. 如图,该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分.若该几何体上、下两个圆的半径分别为1和2,原大圆锥高的剩余部分为 , 则其侧面展开图的面积为( ) A、 B、 C、 D、3. 已知点是等边的边上的一点,若 , 则在以线段为边的三角形中,最小内角的大小为( )A、 B、 C、 D、4. 如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A、 B、 C、 D、3. 已知点是等边的边上的一点,若 , 则在以线段为边的三角形中,最小内角的大小为( )A、 B、 C、 D、4. 如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆相互经过彼此的圆心,则图中三个阴影部分的面积之和为( ) A、 B、 C、 D、5. 如图,在菱形中, , , 动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( )
A、 B、 C、 D、5. 如图,在菱形中, , , 动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( ) A、
A、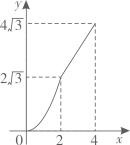 B、
B、 C、
C、 D、
D、 6. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
6. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
① ② ③当时,
A、0个 B、1个 C、2个 D、3个7. 如图,已知等腰直角 , , , 点C是矩形与的公共顶点,且 , ;点D是延长线上一点,且 . 连接 , , 在矩形绕点C按顺时针方向旋转一周的过程中,当线段达到最长和最短时,线段对应的长度分别为m和n,则的值为( ) A、2 B、3 C、 D、
A、2 B、3 C、 D、二、填空题
-
8. 如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
 9. 如图,在中, , 分别以点B和点C为圆心,大于的长为半径作弧,两孤交于点D,作直线交于点E.若 , 则的大小为度.
9. 如图,在中, , 分别以点B和点C为圆心,大于的长为半径作弧,两孤交于点D,作直线交于点E.若 , 则的大小为度.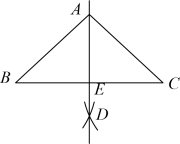 10. 如图,在中, . 点 , 分别在边 , 上,连接 , 将沿折叠,点的对应点为点 . 若点刚好落在边上, , 则的长为 .
10. 如图,在中, . 点 , 分别在边 , 上,连接 , 将沿折叠,点的对应点为点 . 若点刚好落在边上, , 则的长为 . 11. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.
11. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.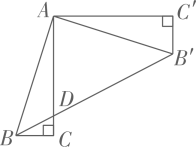 12. 如图,与位于平面直角坐标系中, , , , 若 , 反比例函数恰好经过点C,则 .
12. 如图,与位于平面直角坐标系中, , , , 若 , 反比例函数恰好经过点C,则 . 13. 如图,正八边形的边长为 , 对角线、相交于点则线段的长为 .
13. 如图,正八边形的边长为 , 对角线、相交于点则线段的长为 . 14. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .
14. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .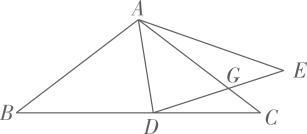 15. 如图,的半径为2 , 为的弦,点C为上的一点,将沿弦翻折,使点C与圆心O重合,则阴影部分的面积为.(结果保留π与根号)
15. 如图,的半径为2 , 为的弦,点C为上的一点,将沿弦翻折,使点C与圆心O重合,则阴影部分的面积为.(结果保留π与根号) 16. 已知等腰 , , .现将以点B为旋转中心旋转45°,得到 , 延长交直线于点D.则的长度为.17. 如图,是边长为6的等边三角形,点E为高上的动点.连接 , 将绕点C顺时针旋转60°得到.连接 , , , 则周长的最小值是.
16. 已知等腰 , , .现将以点B为旋转中心旋转45°,得到 , 延长交直线于点D.则的长度为.17. 如图,是边长为6的等边三角形,点E为高上的动点.连接 , 将绕点C顺时针旋转60°得到.连接 , , , 则周长的最小值是.
三、解答题
-
18. 2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站,如图中的照片展示了中国空间站上机械臂的一种工作状态,当两臂 , 两臂夹角时,求A,B两点间的距离.(结果精确到 , 参考数据 , , )

四、作图题
-
19. 如图,四边形是平行四边形.
 (1)、尺规作图;作对角线的垂直平分线(保留作图痕迹);(2)、若直线分别交 , 于 , 两点,求证:四边形是菱形
(1)、尺规作图;作对角线的垂直平分线(保留作图痕迹);(2)、若直线分别交 , 于 , 两点,求证:四边形是菱形五、综合题
-
20. 如图,一次函数与函数为的图象交于两点.
 (1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.21. 如图,在单位长度为1的网格中,点O,A,B均在格点上, , , 以O为圆心,为半径画圆,请按下列步骤完成作图,并回答问题:
(1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.21. 如图,在单位长度为1的网格中,点O,A,B均在格点上, , , 以O为圆心,为半径画圆,请按下列步骤完成作图,并回答问题: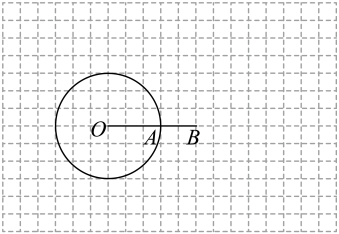
①过点A作切线 , 且(点C在A的上方);
②连接 , 交于点D;
③连接 , 与交于点E.
(1)、求证:为的切线;(2)、求的长度.22. 如图,内接于 , , 过点作的垂线,交于点 , 并与的延长线交于点 , 作 , 垂足为 , 交于点 . (1)、求证:;(2)、若的半径 , , 求线段的长.23. 如图1,点P是线段AB上与点A,点B不重合的任意一点,在AB的同侧分别以A,P,B为顶点作 ∠1=∠2=∠3,其中∠1与∠3的一边分别是射线AB和射线BA,∠2的两边不在直线AB上,我们规定这三个角互为等联角,点P为等联点,线段AB为等联线.
(1)、求证:;(2)、若的半径 , , 求线段的长.23. 如图1,点P是线段AB上与点A,点B不重合的任意一点,在AB的同侧分别以A,P,B为顶点作 ∠1=∠2=∠3,其中∠1与∠3的一边分别是射线AB和射线BA,∠2的两边不在直线AB上,我们规定这三个角互为等联角,点P为等联点,线段AB为等联线.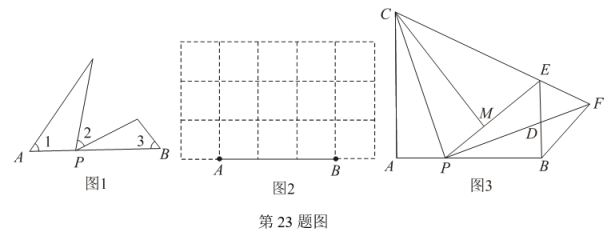 (1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.
(1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.①确定△PCF的形状,并说明理由;
②若AP:PB=1:2,BF=k,求等联线AB和线段PE的长(用含k的式子表示).
24. 如图,点A,B,C在上运动,满足 , 延长至点D,使得 , 点E是弦上一动点(不与点A,C重合),过点E作弦的垂线,交于点F,交的延长线于点N,交于点M(点M在劣弧上).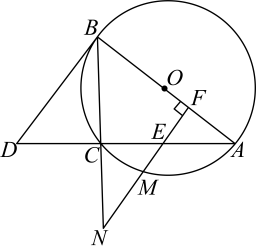 (1)、是的切线吗?请作出你的判断并给出证明;(2)、记的面积分别为 , 若 , 求的值;(3)、若的半径为1,设 , , 试求y关于x的函数解析式,并写出自变量x的取值范围.25. 如图,在正方形中, , 点是对角线的中点,动点 , 分别从点 , 同时出发,点以的速度沿边向终点匀速运动,点以的速度沿折线向终点匀速运动.连接并延长交边于点 , 连接并延长交折线于点 , 连接 , , , , 得到四边形 . 设点的运动时间为()(),四边形的面积为()
(1)、是的切线吗?请作出你的判断并给出证明;(2)、记的面积分别为 , 若 , 求的值;(3)、若的半径为1,设 , , 试求y关于x的函数解析式,并写出自变量x的取值范围.25. 如图,在正方形中, , 点是对角线的中点,动点 , 分别从点 , 同时出发,点以的速度沿边向终点匀速运动,点以的速度沿折线向终点匀速运动.连接并延长交边于点 , 连接并延长交折线于点 , 连接 , , , , 得到四边形 . 设点的运动时间为()(),四边形的面积为()
 (1)、的长为 , 的长为 . (用含x的代数式表示)(2)、求关于的函数解析式,并写出自变量的取值范围.(3)、当四边形是轴对称图形时,直接写出的值.26. 如图,在菱形ABCD中,对角线AC,BD相交于点 , 点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点.
(1)、的长为 , 的长为 . (用含x的代数式表示)(2)、求关于的函数解析式,并写出自变量的取值范围.(3)、当四边形是轴对称图形时,直接写出的值.26. 如图,在菱形ABCD中,对角线AC,BD相交于点 , 点P,Q分别是边BC,线段OD上的点,连接AP,QP,AP与OB相交于点. (1)、如图1,连接QA.当时,试判断点是否在线段PC的垂直平分线上,并说明理由;(2)、如图2, , 且 ,
(1)、如图1,连接QA.当时,试判断点是否在线段PC的垂直平分线上,并说明理由;(2)、如图2, , 且 ,①求证:;
②当时,设 , 求PQ的长(用含a的代数式表示).
27. 综合运用如图1,在平面直角坐标系中,正方形的顶点A在轴的正半轴上,如图2,将正方形绕点逆时针旋转,旋转角为 , 交直线于点 , 交轴于点 .
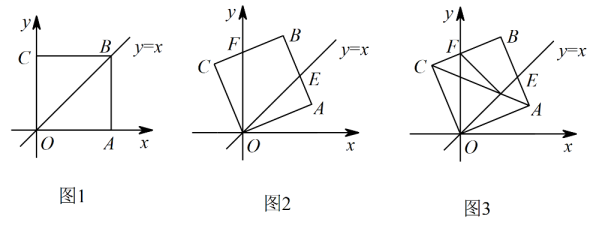 (1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.28. 综合与实践
(1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.28. 综合与实践数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
 (1)、发现问题:如图1,在和中, , , , 连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系: , °;(2)、类比探究:如图2,在和中, , , , 连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及的度数,并说明理由;(3)、拓展延伸:如图3,和均为等腰直角三角形, , 连接BE,CF,且点B,E,F在一条直线上,过点A作 , 垂足为点M.则BF,CF,AM之间的数量关系:;(4)、实践应用:正方形ABCD中, , 若平面内存在点P满足 , , 则.
(1)、发现问题:如图1,在和中, , , , 连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系: , °;(2)、类比探究:如图2,在和中, , , , 连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及的度数,并说明理由;(3)、拓展延伸:如图3,和均为等腰直角三角形, , 连接BE,CF,且点B,E,F在一条直线上,过点A作 , 垂足为点M.则BF,CF,AM之间的数量关系:;(4)、实践应用:正方形ABCD中, , 若平面内存在点P满足 , , 则.
-
-