2023年中考数学真题分类汇编(全国版):三角形(3)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点外接圆的一部分,小正方形边长为1,图中阴影部分的面积为( )
 A、 B、 C、 D、2. 如图,在中, , 点在边上,且平分的周长,则的长是( )
A、 B、 C、 D、2. 如图,在中, , 点在边上,且平分的周长,则的长是( )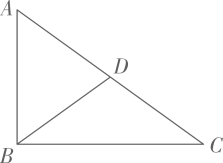 A、 B、 C、 D、3. 如图,在中, , , . 点F是中点,连接 , 把线段沿射线方向平移到 , 点D在上.则线段在平移过程中扫过区域形成的四边形的周长和面积分别是( )
A、 B、 C、 D、3. 如图,在中, , , . 点F是中点,连接 , 把线段沿射线方向平移到 , 点D在上.则线段在平移过程中扫过区域形成的四边形的周长和面积分别是( ) A、16,6 B、18,18 C、16,12 D、12,164. 如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M, , 则下列结论,① , ② , ③ , ④ . 正确的是( )
A、16,6 B、18,18 C、16,12 D、12,164. 如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M, , 则下列结论,① , ② , ③ , ④ . 正确的是( ) A、①②③ B、②④ C、①③④ D、①②③④5. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( )
A、①②③ B、②④ C、①③④ D、①②③④5. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( ) A、 B、 C、 D、6. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( )
A、 B、 C、 D、6. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( ) A、 B、 C、 D、7. 如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为x, , 图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为( )
A、 B、 C、 D、7. 如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为x, , 图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为( ) A、6 B、3 C、 D、8. 如图, , 是的弦, , 是的半径,点为上任意一点(点不与点重合),连接 . 若 , 则的度数可能是( )
A、6 B、3 C、 D、8. 如图, , 是的弦, , 是的半径,点为上任意一点(点不与点重合),连接 . 若 , 则的度数可能是( ) A、 B、 C、 D、9. 下图源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为 , 则的值为( )
A、 B、 C、 D、9. 下图源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 在平面直角坐标系中,若反比例函数的图象经过点和点 , 则的面积为 .11. 如图,和都是等腰直角三角形, , 点在内, , 连接交于点交于点 , 连接 . 给出下面四个结论:①;②;③;④ . 其中所有正确结论的序号是 .
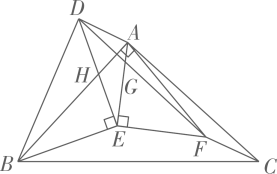 12. 在中, , 点是斜边的中点,把绕点顺时针旋转,得 , 点 , 点旋转后的对应点分别是点 , 点 , 连接 , , 在旋转的过程中,面积的最大值是 .
12. 在中, , 点是斜边的中点,把绕点顺时针旋转,得 , 点 , 点旋转后的对应点分别是点 , 点 , 连接 , , 在旋转的过程中,面积的最大值是 .
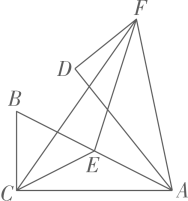 13. 矩形ABCD中,M为对角线BD的中点,点N在边AD上,且 . 当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .14. 如图,PA与相切于点A,PO交于点B,点C在PA上,且 . 若 , , 则CA的长为 .
13. 矩形ABCD中,M为对角线BD的中点,点N在边AD上,且 . 当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .14. 如图,PA与相切于点A,PO交于点B,点C在PA上,且 . 若 , , 则CA的长为 .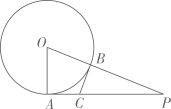 15. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上, . “会圆术”给出长l的近似值s计算公式: , 当 , 时, . (结果保留一位小数)
15. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上, . “会圆术”给出长l的近似值s计算公式: , 当 , 时, . (结果保留一位小数) 16. 如图,矩形中, , 点P在对角线上,过点P作 , 交边于点M,N,过点M作交于点E,连接 . 下列结论:①;②四边形的面积不变;③当时,;④的最小值是20.其中所有正确结论的序号是 .
16. 如图,矩形中, , 点P在对角线上,过点P作 , 交边于点M,N,过点M作交于点E,连接 . 下列结论:①;②四边形的面积不变;③当时,;④的最小值是20.其中所有正确结论的序号是 . 17. 如图,在中,的内切圆与分别相切于点 , , 连接的延长线交于点 , 则 .
17. 如图,在中,的内切圆与分别相切于点 , , 连接的延长线交于点 , 则 . 18. 如图,抛物线与x轴交于点A,B,与y轴交于点C,点在抛物线上,点E在直线上,若 , 则点E的坐标是 .
18. 如图,抛物线与x轴交于点A,B,与y轴交于点C,点在抛物线上,点E在直线上,若 , 则点E的坐标是 .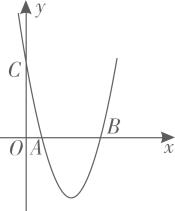 19. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
19. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
三、解答题
-
20. 如图,点C在线段上,在和中, .
求证: .

四、作图题
-
21. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段的端点均在格点上.在图①、图②、图③中以为边各画一个等腰三角形,使其依次为锐角三角形、直角三角形、钝角三角形,且所画三角形的顶点均在格点上.
 22. 如图已知角 , , 请用尺规作图法,在内部求作一点使且保留作图痕迹,不写作法
22. 如图已知角 , , 请用尺规作图法,在内部求作一点使且保留作图痕迹,不写作法
五、综合题
-
23. 如图,已知是等边三角形的外接圆,连接并延长交于点 , 交于点 , 连接 , .
 (1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.24. 如图,在平面直角坐标系中,点在第一象限内,与轴相切于点 , 与轴相交于点 , . 连接 , .
(1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.24. 如图,在平面直角坐标系中,点在第一象限内,与轴相切于点 , 与轴相交于点 , . 连接 , . (1)、求点的坐标;(2)、求的值.25. 两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扇圆型器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系.
(1)、求点的坐标;(2)、求的值.25. 两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扇圆型器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系. (1)、若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为;(2)、利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).
(1)、若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为;(2)、利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
26. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作 , 连接BF. (1)、求k的值;(2)、求扇形AOC的半径及圆心角的度数;(3)、请直接写出图中阴影部分面积之和.27. 如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形中, , 过点作射线 , 垂足为 , 点在上.
(1)、求k的值;(2)、求扇形AOC的半径及圆心角的度数;(3)、请直接写出图中阴影部分面积之和.27. 如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形中, , 过点作射线 , 垂足为 , 点在上. (1)、【动手操作】
(1)、【动手操作】如图②,若点在线段上,画出射线 , 并将射线绕点逆时针旋转与交于点 , 根据题意在图中画出图形 , 图中的度数为度;
(2)、【问题探究】根据(1)所画图形,探究线段与的数量关系,并说明理由;
(3)、【拓展延伸】如图③,若点在射线上移动,将射线绕点逆时针旋转与交于点 , 探究线段之间的数量关系,并说明理由.
28. 如图1,在平面直角坐标系中,直线l⊥y轴,交y轴的正半轴于点A,且OA=2,点B是y轴右侧直线l上的一动点,连接OB. (1)、请直接写出点A的坐标;(2)、如图2,若动点B满足∠ABO=30°,点C为AB的中点,D点为线段OB上一动点,连接CD.在平面内,将△BCD沿CD翻折,点B的对应点为点P,CP与OB相交于点Q,当CP⊥AB时,求线段DQ的长;(3)、如图3,若动点B满足=2,EF为△OAB的中位线,将△BEF绕点B在平面内逆时针旋转,当点O、E、F三点共线时,求直线EB与x轴交点的坐标;(4)、如图4,OC平分∠AOB交AB于点C,AD⊥OB于点D,交OC于点E,AF为△AEC的一条中线.设△ACF,△ODE,△OAC的周长分别为C1 , C2 , C3 . 试探究:在B点的运动过程中,当时,请直接写出点B的坐标.29. 【阅读理解】如图1,在矩形中,若 , 由勾股定理,得 , 同理 , 故 .
(1)、请直接写出点A的坐标;(2)、如图2,若动点B满足∠ABO=30°,点C为AB的中点,D点为线段OB上一动点,连接CD.在平面内,将△BCD沿CD翻折,点B的对应点为点P,CP与OB相交于点Q,当CP⊥AB时,求线段DQ的长;(3)、如图3,若动点B满足=2,EF为△OAB的中位线,将△BEF绕点B在平面内逆时针旋转,当点O、E、F三点共线时,求直线EB与x轴交点的坐标;(4)、如图4,OC平分∠AOB交AB于点C,AD⊥OB于点D,交OC于点E,AF为△AEC的一条中线.设△ACF,△ODE,△OAC的周长分别为C1 , C2 , C3 . 试探究:在B点的运动过程中,当时,请直接写出点B的坐标.29. 【阅读理解】如图1,在矩形中,若 , 由勾股定理,得 , 同理 , 故 .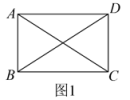 (1)、【探究发现】如图2,四边形为平行四边形,若 , 则上述结论是否依然成立?请加以判断,并说明理由.
(1)、【探究发现】如图2,四边形为平行四边形,若 , 则上述结论是否依然成立?请加以判断,并说明理由. (2)、【拓展提升】如图3,已知为的一条中线, . 求证: .
(2)、【拓展提升】如图3,已知为的一条中线, . 求证: . (3)、【尝试应用】如图4,在矩形中,若 , 点P在边上,则的最小值为 .
(3)、【尝试应用】如图4,在矩形中,若 , 点P在边上,则的最小值为 . 30. 数学兴趣小组探究了以下几何图形.如图①,把一个含有角的三角尺放在正方形中,使角的顶点始终与正方形的顶点重合,绕点旋转三角尺时,角的两边 , 始终与正方形的边 , 所在直线分别相交于点 , , 连接 , 可得 .
30. 数学兴趣小组探究了以下几何图形.如图①,把一个含有角的三角尺放在正方形中,使角的顶点始终与正方形的顶点重合,绕点旋转三角尺时,角的两边 , 始终与正方形的边 , 所在直线分别相交于点 , , 连接 , 可得 .
 (1)、【探究一】
(1)、【探究一】如图②,把绕点C逆时针旋转得到 , 同时得到点在直线上.求证:;
(2)、【探究二】在图②中,连接 , 分别交 , 于点 , . 求证:;
(3)、【探究三】把三角尺旋转到如图③所示位置,直线与三角尺角两边 , 分别交于点 , . 连接交于点 , 求的值.
-