2023年中考数学真题分类汇编(全国版):三角形(2)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 已知直角三角形的三边满足 , 分别以为边作三个正方形,把两个较小的正方形放置在最大正方形内,如图,设三个正方形无重叠部分的面积为 , 均重叠部分的面积为 , 则( )
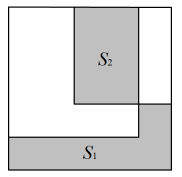 A、 B、 C、 D、大小无法确定2. 5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为 , 腰长为 , 则底边上的高是( )
A、 B、 C、 D、大小无法确定2. 5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为 , 腰长为 , 则底边上的高是( ) A、 B、 C、 D、3. 如图,为等边三角形,点 , 分别在边 , 上, , 若 , , 则的长为( )
A、 B、 C、 D、3. 如图,为等边三角形,点 , 分别在边 , 上, , 若 , , 则的长为( ) A、 B、 C、 D、4. 如图,在平面直角坐标系中,菱形的边长为 , 点在轴的正半轴上,且 , 将菱形绕原点逆时针方向旋转 , 得到四边形点与点重合 , 则点的坐标是( )
A、 B、 C、 D、4. 如图,在平面直角坐标系中,菱形的边长为 , 点在轴的正半轴上,且 , 将菱形绕原点逆时针方向旋转 , 得到四边形点与点重合 , 则点的坐标是( )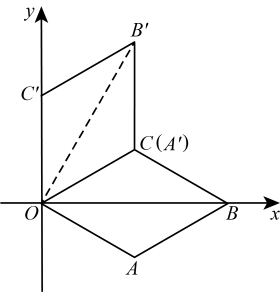 A、 B、 C、 D、5. 在中, , 下列说法错误的是( )A、 B、 C、内切圆的半径 D、当时,是直角三角形6. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )
A、 B、 C、 D、5. 在中, , 下列说法错误的是( )A、 B、 C、内切圆的半径 D、当时,是直角三角形6. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )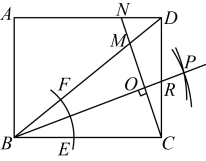 A、 B、 C、 D、47. 如图,正方形的边长为4,点 , 分别在边 , 上,且 , 平分 , 连接 , 分别交 , 于点 , , 是线段上的一个动点,过点作垂足为 , 连接 , 有下列四个结论:①垂直平分;②的最小值为;③;④ . 其中正确的是( )
A、 B、 C、 D、47. 如图,正方形的边长为4,点 , 分别在边 , 上,且 , 平分 , 连接 , 分别交 , 于点 , , 是线段上的一个动点,过点作垂足为 , 连接 , 有下列四个结论:①垂直平分;②的最小值为;③;④ . 其中正确的是( ) A、①② B、②③④ C、①③④ D、①③8. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )
A、①② B、②③④ C、①③④ D、①③8. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )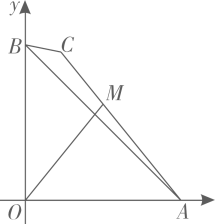 A、( , ) B、( , ) C、( , ) D、( , )
A、( , ) B、( , ) C、( , ) D、( , )二、填空题
-
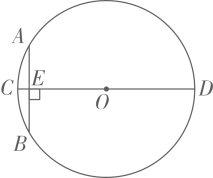
9. 若一个三角形的边长均为整数,且两边长分别为3和5,则第三边的长可以为(写出一个即可).10. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”.用现在的几何语言表达即:如图,为的直径,弦 , 垂足为点 , 寸,寸,则直径的长度是寸.
 11. 如图,在中,以点为圆心,任意长为半径作弧,分别交 , 于点 , ;分别以点 , 为圆心,大于的长为半径作弧,两弧交于点;作射线交于点 , 若 , , 的面积为 , 则的面积为 .
11. 如图,在中,以点为圆心,任意长为半径作弧,分别交 , 于点 , ;分别以点 , 为圆心,大于的长为半径作弧,两弧交于点;作射线交于点 , 若 , , 的面积为 , 则的面积为 . 12. 如图,在正方形中,分别以点为圆心,以的长为半径画弧,两弧交于点 , 连接 , 则 .
12. 如图,在正方形中,分别以点为圆心,以的长为半径画弧,两弧交于点 , 连接 , 则 . 13. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1·k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是 .
13. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1·k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是 . 14. 2002年的国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图,世人称之为“赵爽弦图”.如图,用四个全等的直角三角形(Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA)拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,连接AC和EG,AC与DF、EG、BH分别相交于点P、O、Q,若BE∶EQ=3∶2,则的值是 .
14. 2002年的国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图,世人称之为“赵爽弦图”.如图,用四个全等的直角三角形(Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA)拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,连接AC和EG,AC与DF、EG、BH分别相交于点P、O、Q,若BE∶EQ=3∶2,则的值是 . 15. 如图,在中, , 点在边上.将沿折叠,使点落在点处,连接 , 则的最小值为 .
15. 如图,在中, , 点在边上.将沿折叠,使点落在点处,连接 , 则的最小值为 . 16. 如图,在中,直径与弦交于点 . 连接 , 过点的切线与的延长线交于点 . 若 , 则°.
16. 如图,在中,直径与弦交于点 . 连接 , 过点的切线与的延长线交于点 . 若 , 则°.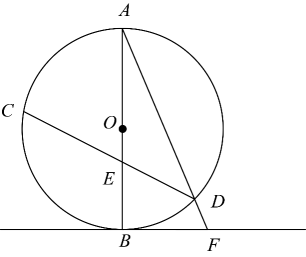 17. 如图,在矩形中,点为矩形内一点,且 , , 则四边形的面积是 .
17. 如图,在矩形中,点为矩形内一点,且 , , 则四边形的面积是 .
三、解答题
-
18. 如图①,和是等边三角形,连接 , 点F,G,H分别是和的中点,连接 . 易证: .
若和都是等腰直角三角形,且 , 如图②:若和都是等腰三角形,且 , 如图③:其他条件不变,判断和之间的数量关系,写出你的猜想,并利用图②或图③进行证明.

四、作图题
-
19. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , .
 (1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).20. 如图,中,点D在边AC上,且 .
(1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).20. 如图,中,点D在边AC上,且 . (1)、请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).(2)、若(1)中所作的角平分线与边BC交于点E,连接DE.求证: .
(1)、请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).(2)、若(1)中所作的角平分线与边BC交于点E,连接DE.求证: .五、综合题
-
21. 如图,中,点D、E分别为的中点,延长到点F,使得 , 连接 . 求证:
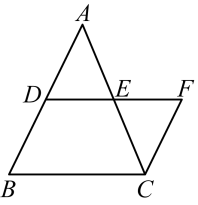 (1)、;(2)、四边形是平行四边形.22. 如图,矩形的对角线与相交于点O, , 直线是线段的垂直平分线,分别交于点F,G,连接 .
(1)、;(2)、四边形是平行四边形.22. 如图,矩形的对角线与相交于点O, , 直线是线段的垂直平分线,分别交于点F,G,连接 . (1)、判断四边形的形状,并说明理由;(2)、当时,求的长.23. 综合与实践(1)、问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得 , 连接 , 以为边作等边三角形 , 则就是的平分线.
(1)、判断四边形的形状,并说明理由;(2)、当时,求的长.23. 综合与实践(1)、问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得 , 连接 , 以为边作等边三角形 , 则就是的平分线.
请写出平分的依据:;
(2)、类比迁移:
小明根据以上信息研究发现:不一定必须是等边三角形,只需即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在的边 , 上分别取 , 移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线是的平分线,请说明此做法的理由;
(3)、拓展实践:
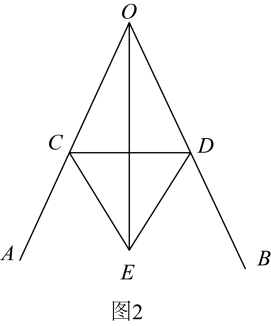
小明将研究应用于实践.如图4,校园的两条小路和 , 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
24. 如图,平行四边形中,点E是对角线上一点,连接 , 且 . (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.25. 如图,在中, , 延长至D,使得 , 过点A,D分别作 , , 与相交于点E.下面是两位同学的对话:
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.25. 如图,在中, , 延长至D,使得 , 过点A,D分别作 , , 与相交于点E.下面是两位同学的对话: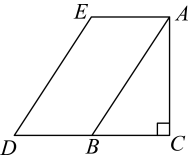

小星:由题目的已知条件,若连接 , 则可
证明 .
小红:由题目的已知条件,若连接 , 则可证明 .
 (1)、请你选择一位同学的说法,并进行证明;(2)、连接 , 若 , 求的长.26. 在平面直角坐标系中,给出如下定义:为图形上任意一点,如果点到直线的距离等于图形上任意两点距离的最大值时,那么点称为直线的“伴随点”.
(1)、请你选择一位同学的说法,并进行证明;(2)、连接 , 若 , 求的长.26. 在平面直角坐标系中,给出如下定义:为图形上任意一点,如果点到直线的距离等于图形上任意两点距离的最大值时,那么点称为直线的“伴随点”.例如:如图1,已知点 , , 在线段上,则点是直线:轴的“伴随点”.
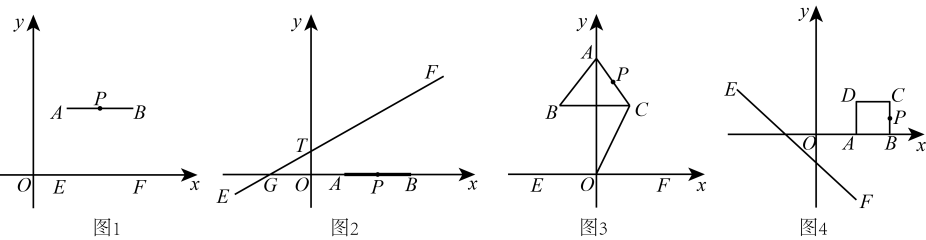 (1)、如图2,已知点 , , 是线段上一点,直线过 , 两点,当点是直线的“伴随点”时,求点的坐标;(2)、如图3,轴上方有一等边三角形 , 轴,顶点在轴上且在上方, , 点是上一点,且点是直线:轴的伴随点 . 当点到轴的距离最小时,求等边三角形的边长;(3)、如图4,以 , , 为顶点的正方形上始终存在点 , 使得点是直线:的伴随点 . 请直接写出的取值范围.27. 综合与实践
(1)、如图2,已知点 , , 是线段上一点,直线过 , 两点,当点是直线的“伴随点”时,求点的坐标;(2)、如图3,轴上方有一等边三角形 , 轴,顶点在轴上且在上方, , 点是上一点,且点是直线:轴的伴随点 . 当点到轴的距离最小时,求等边三角形的边长;(3)、如图4,以 , , 为顶点的正方形上始终存在点 , 使得点是直线:的伴随点 . 请直接写出的取值范围.27. 综合与实践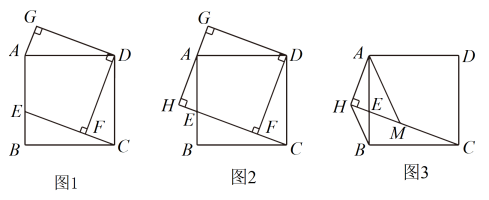 (1)、【思考尝试】
(1)、【思考尝试】数学活动课上,老师出示了一个问题:如图1,在矩形ABCD中,E是边上一点,于点F, , , . 试猜想四边形的形状,并说明理由;
(2)、【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形中,E是边上一点,于点F,于点H,交于点G,可以用等式表示线段 , , 的数量关系,请你思考并解答这个问题;
(3)、【拓展迁移】小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图3,在正方形中,E是边上一点,于点H,点M在上,且 , 连接 , , 可以用等式表示线段 , 的数量关系,请你思考并解答这个问题.
28. 如图,已知是的直径, , 切于点 , 过点作交于点 , 若 . (1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.
(1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.
-