2023年中考数学真题分类汇编(全国版):相交线与平行线(4)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,在正方形网格内,线段的两个端点都在格点上,网格内另有四个格点,下面四个结论中,正确的是( )
 A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则2. 如图,已知 , 则的度数是( )
A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则2. 如图,已知 , 则的度数是( )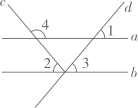 A、 B、 C、 D、3. 如图, , 若 , 则的度数为( )
A、 B、 C、 D、3. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、4. 如图,切于点B,连接交于点C,交于点D,连接 , 若 , 则的度数为( )
A、 B、 C、 D、4. 如图,切于点B,连接交于点C,交于点D,连接 , 若 , 则的度数为( ) A、 B、 C、 D、5. 如图, , 且 , , 则等于( )
A、 B、 C、 D、5. 如图, , 且 , , 则等于( ) A、 B、 C、 D、6. 如图, , 平分 , 则( )
A、 B、 C、 D、6. 如图, , 平分 , 则( ) A、 B、 C、 D、7. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, , 则( )
A、 B、 C、 D、7. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, , 则( ) A、 B、 C、 D、8. 如图,某人沿路线行走,与方向相同, , 则( )
A、 B、 C、 D、8. 如图,某人沿路线行走,与方向相同, , 则( )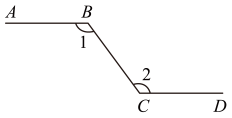 A、 B、 C、 D、9. 如图, , 若 , 则的度数为( )
A、 B、 C、 D、9. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、10. 如图,直线 , 被直线所截,若 , , 则的度数为( ).
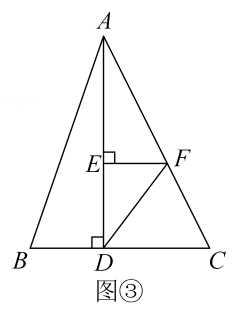
A、 B、 C、 D、10. 如图,直线 , 被直线所截,若 , , 则的度数为( ).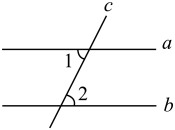 A、 B、 C、 D、11. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( )
A、 B、 C、 D、11. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( ) A、的面积 B、的面积 C、的面积 D、的面积12. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )
A、的面积 B、的面积 C、的面积 D、的面积12. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )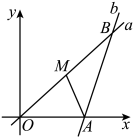 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,点O在直线AB上,OD是的平分线,若 , 则的度数为 .
 14. 如图,在中,D是边AB上一点,按以下步骤作图:①以点A为圆心,以适当长为半径作弧,分别交AB,AC于点M,N;②以点D为圆心,以AM长为半径作弧,交DB于点;③以点为圆心,以MN长为半径作弧,在内部交前面的弧于点;④过点作射线交BC于点E. 若与四边形ACED的面积比为4:21,则的值为.
14. 如图,在中,D是边AB上一点,按以下步骤作图:①以点A为圆心,以适当长为半径作弧,分别交AB,AC于点M,N;②以点D为圆心,以AM长为半径作弧,交DB于点;③以点为圆心,以MN长为半径作弧,在内部交前面的弧于点;④过点作射线交BC于点E. 若与四边形ACED的面积比为4:21,则的值为.
三、解答题
-
15. 如图,点在线段上, , , . 求证: .

四、综合题
-
16. 如图,中,点E是的中点,连接并延长交的延长线于点F.
 (1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.17. 如图,是的直径,是上一点,过点作的切线 , 交的延长线于点 , 过点作于点.
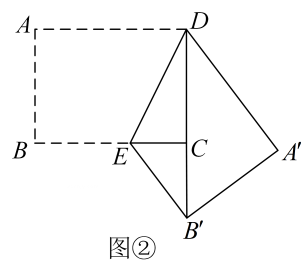
(1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.17. 如图,是的直径,是上一点,过点作的切线 , 交的延长线于点 , 过点作于点. (1)、若 , 求的度数.(2)、若 , 求的长.18. 如图,在正方形中,是对角线上的一点(与点不重合),分别为垂足.连结 , 并延长交于点.
(1)、若 , 求的度数.(2)、若 , 求的长.18. 如图,在正方形中,是对角线上的一点(与点不重合),分别为垂足.连结 , 并延长交于点. (1)、求证:.(2)、判断与是否垂直,并说明理由.19. 如图,四边形中, , 点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)、求证:.(2)、判断与是否垂直,并说明理由.19. 如图,四边形中, , 点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合) (1)、求证:;(2)、当直线时,连接、 , 试判断四边形的形状,并说明理由.20. 如图,以的边AC为直径作 , 交BC边于点D,过点C作交于点E,连接AD,DE,.
(1)、求证:;(2)、当直线时,连接、 , 试判断四边形的形状,并说明理由.20. 如图,以的边AC为直径作 , 交BC边于点D,过点C作交于点E,连接AD,DE,. (1)、求证:;(2)、若 , , 求AB和DE的长.21. 如图,等腰内接于 , , 是边上的中线,过点作的平行线交的延长线于点 , 交于点 , 连接 .
(1)、求证:;(2)、若 , , 求AB和DE的长.21. 如图,等腰内接于 , , 是边上的中线,过点作的平行线交的延长线于点 , 交于点 , 连接 . (1)、求证:为的切线;(2)、若的半径为 , , 求的长.22. 如图,中,以为直径的交于点E.平分 , 过点E作于点D,延长交的延长线于点P.
(1)、求证:为的切线;(2)、若的半径为 , , 求的长.22. 如图,中,以为直径的交于点E.平分 , 过点E作于点D,延长交的延长线于点P.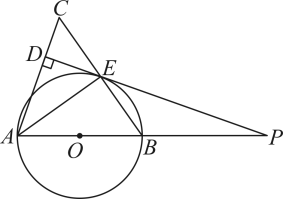 (1)、求证:是的切线;(2)、若 , 求的长.
(1)、求证:是的切线;(2)、若 , 求的长.
-