2023年中考数学真题分类汇编(全国版):相交线与平行线(3)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
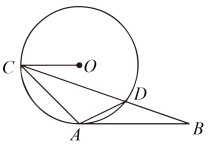
1. 如图,是的直径,点C,D在上,连接 , 若 , 则的度数是( )
 A、 B、 C、 D、2. 如图,平移直线至 , 直线 , 被直线所截, , 则的度数为( )
A、 B、 C、 D、2. 如图,平移直线至 , 直线 , 被直线所截, , 则的度数为( )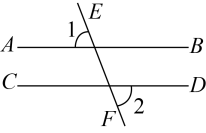 A、 B、 C、 D、3. 如图,直线被直线所截,已知 , 则的大小为( )
A、 B、 C、 D、3. 如图,直线被直线所截,已知 , 则的大小为( )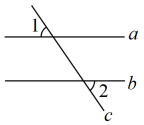 A、 B、 C、 D、4. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )
A、 B、 C、 D、4. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )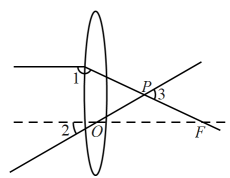 A、 B、 C、 D、5. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( )
A、 B、 C、 D、5. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( ) A、1 B、 C、2 D、36. 如图,直线 , 直线l与、相交,若图中 , 则为( )
A、1 B、 C、2 D、36. 如图,直线 , 直线l与、相交,若图中 , 则为( ) A、 B、 C、 D、7. 如图,在中,分别以B,D为圆心,大于的长为半径画弧,两弧相交于点M,N,过M,N两点作直线交于点O,交于点E,F,下列结论不正确的是( )
A、 B、 C、 D、7. 如图,在中,分别以B,D为圆心,大于的长为半径画弧,两弧相交于点M,N,过M,N两点作直线交于点O,交于点E,F,下列结论不正确的是( )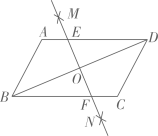 A、 B、 C、 D、8. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ).
A、 B、 C、 D、8. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ). A、 B、 C、 D、9. 如图,在四边形中, , 若添加一个条件,使四边形为平形四边形,则下列正确的是( )
A、 B、 C、 D、9. 如图,在四边形中, , 若添加一个条件,使四边形为平形四边形,则下列正确的是( )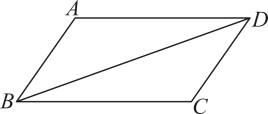 A、 B、 C、 D、10. 如图,分别过的顶点A,B作 . 若 , , 则的度数为( )
A、 B、 C、 D、10. 如图,分别过的顶点A,B作 . 若 , , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
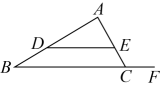
11. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .
 12. 一杆古秤在称物时的状态如图所示,已知 , 则的度数为 .
12. 一杆古秤在称物时的状态如图所示,已知 , 则的度数为 . 13. 用一张等宽的纸条折成如图所示的图案,若 , 则∠2的度数为 .
13. 用一张等宽的纸条折成如图所示的图案,若 , 则∠2的度数为 . 14. 如图,点是正方形的对角线上的一点,于点 , . 则点到直线的距离为 .
14. 如图,点是正方形的对角线上的一点,于点 , . 则点到直线的距离为 .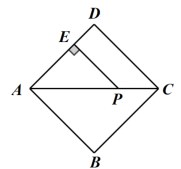 15. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).
15. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).
三、解答题
-
16. 已知:如图, , , . 求证: .

四、作图题
-
17. 如图,为制作角度尺,将长为10,宽为4的矩形OABC分割成4×10的小正方形网格.在该矩形边上取点P,来表示∠POA的度数.阅读以下作图过程,并回答下列问题:
作法(如图)
结论
①在上取点 , 使.
,
点表示.
②以为圆心,8为半径作弧,与交于点
,
点表示.
③分别以 , 为圆心,大于长度一半的长为半径作弧,相交于点E,F,连结EF与BC相交于点.
…
④以为圆心,的长为半径作弧,与射线交于点 , 连结交于点.
…
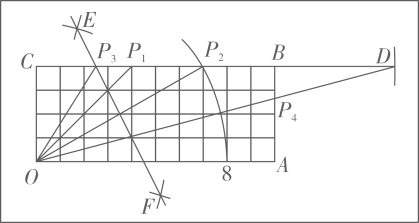 (1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).
(1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).五、综合题
-
18. 如图所示,在某交叉路口,一货车在道路①上点A处等候“绿灯”一辆车从被山峰遮挡的道路②上的点B处由南向北行驶.已知 , , 线段的延长线交直线于点D.
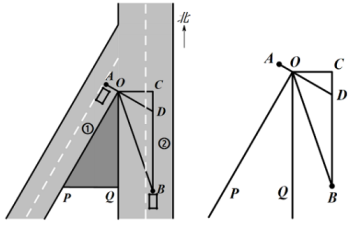 (1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)19. 如图,在中,D是的中点,E是的中点,过点A作交的延长线于点F.
(1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)19. 如图,在中,D是的中点,E是的中点,过点A作交的延长线于点F.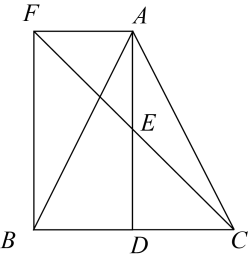 (1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.20. 如图,已知内接于的延长线交于点 , 交于点 , 交的切线于点 , 且 .
(1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.20. 如图,已知内接于的延长线交于点 , 交于点 , 交的切线于点 , 且 . (1)、求证:;(2)、求证:平分 .21. 如图,在四边形中, , 点在的延长线上,连接 .
(1)、求证:;(2)、求证:平分 .21. 如图,在四边形中, , 点在的延长线上,连接 . (1)、求证:;(2)、若平分 , 直接写出的形状.22. 如图,以的直角边为直径作 , 交斜边于点 , 点是的中点,连接 .
(1)、求证:;(2)、若平分 , 直接写出的形状.22. 如图,以的直角边为直径作 , 交斜边于点 , 点是的中点,连接 . (1)、求证:是的切线.(2)、若 , 求的长.(3)、求证: .23. 如图,在中,点 , 在对角线上, . 求证:
(1)、求证:是的切线.(2)、若 , 求的长.(3)、求证: .23. 如图,在中,点 , 在对角线上, . 求证: (1)、;(2)、 .24. 如图,以线段为直径作 , 交射线于点C,平分交于点D,过点D作直线 , 交的延长线于点E,交的延长线于点F.连接并延长交的延长线于点M.
(1)、;(2)、 .24. 如图,以线段为直径作 , 交射线于点C,平分交于点D,过点D作直线 , 交的延长线于点E,交的延长线于点F.连接并延长交的延长线于点M. (1)、求证:直线是的切线;(2)、当时,判断的形状,并说明理由;(3)、在(2)的条件下, , 连接交于点P,求的长.
(1)、求证:直线是的切线;(2)、当时,判断的形状,并说明理由;(3)、在(2)的条件下, , 连接交于点P,求的长.
-
-