2023年中考数学真题分类汇编(全国版):相交线与平行线(2)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图,直线 , 直线与直线a,b分别相交于点A,B,点在直线上,且 , 若 , 则的度数为( )
 A、 B、 C、 D、2. 如图为商场某品牌椅子的侧面图, , 与地面平行, , 则( )
A、 B、 C、 D、2. 如图为商场某品牌椅子的侧面图, , 与地面平行, , 则( ) A、70° B、65° C、60° D、50°3. 如图,街道与平行,拐角 , 则拐角 ( )
A、70° B、65° C、60° D、50°3. 如图,街道与平行,拐角 , 则拐角 ( ) A、 B、 C、 D、4. 如图,直线 , 分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若 , 则的度数是( )
A、 B、 C、 D、4. 如图,直线 , 分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若 , 则的度数是( ) A、 B、 C、 D、5. 如图,在四边形中, , , . 按下列步骤作图:①以点D为圆心,适当长度为半径画弧,分别交于E,F两点;②分别以点E,F为圆心以大于的长为半径画弧,两弧交于点P;③连接并延长交于点G.则的长是( )
A、 B、 C、 D、5. 如图,在四边形中, , , . 按下列步骤作图:①以点D为圆心,适当长度为半径画弧,分别交于E,F两点;②分别以点E,F为圆心以大于的长为半径画弧,两弧交于点P;③连接并延长交于点G.则的长是( ) A、2 B、3 C、4 D、56. 如图, , 点在线段上(不与点 , 重合),连接 , 若 , , 则( )
A、2 B、3 C、4 D、56. 如图, , 点在线段上(不与点 , 重合),连接 , 若 , , 则( ) A、 B、 C、 D、7. 如图,直线AB∥CD,GE⊥EF于点E.若∠BGE=60°,则∠EFD的度数是( )
A、 B、 C、 D、7. 如图,直线AB∥CD,GE⊥EF于点E.若∠BGE=60°,则∠EFD的度数是( ) A、60° B、30° C、40° D、70°8. 如图,在中,为的中点.若点在边上,且 , 则的长为( )
A、60° B、30° C、40° D、70°8. 如图,在中,为的中点.若点在边上,且 , 则的长为( )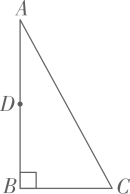 A、1 B、2 C、1或 D、1或29. 如图1,在正方形中,对角线相交于点O,E,F分别为 , 上的一点,且 , 连接 . 若 , 则的度数为( )
A、1 B、2 C、1或 D、1或29. 如图1,在正方形中,对角线相交于点O,E,F分别为 , 上的一点,且 , 连接 . 若 , 则的度数为( )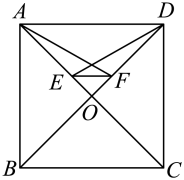 A、 B、 C、 D、10. 下列命题中叙述正确的是( )A、若方差 , 则甲组数据的波动较小 B、直线外一点到这条直线的垂线段,叫做点到直线的距离 C、三角形三条中线的交点叫做三角形的内心 D、角的内部到角的两边的距离相等的点在角的平分线上11. 如图, , 若 , 则的度数为( )
A、 B、 C、 D、10. 下列命题中叙述正确的是( )A、若方差 , 则甲组数据的波动较小 B、直线外一点到这条直线的垂线段,叫做点到直线的距离 C、三角形三条中线的交点叫做三角形的内心 D、角的内部到角的两边的距离相等的点在角的平分线上11. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、12. 如图所示的“箭头”图形中,AB∥CD, , 则图中∠G的度数是( )
A、 B、 C、 D、12. 如图所示的“箭头”图形中,AB∥CD, , 则图中∠G的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,在平行四边形中, , , 的平分线交于点E,则的长为 .
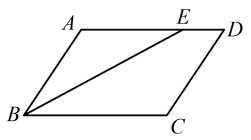 14. 如图, , 直线l与直线a,b分别交于B,A两点,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点E,F,作直线 , 分别交直线a,b于点C,D,连接AC,若 , 则的度数为 .
14. 如图, , 直线l与直线a,b分别交于B,A两点,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点E,F,作直线 , 分别交直线a,b于点C,D,连接AC,若 , 则的度数为 .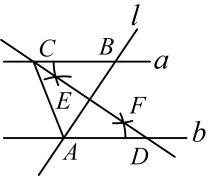 15. 如图,在中,的垂直平分线交于点 , 交于点O,连接 , , 过点C作 , 交的延长线于点F,连接 . 若 , , 则四边形的面积为 .
15. 如图,在中,的垂直平分线交于点 , 交于点O,连接 , , 过点C作 , 交的延长线于点F,连接 . 若 , , 则四边形的面积为 . .16. 如图1,在中, , , , D是上一点,且 , 过点D作交于E,将绕A点顺时针旋转到图2的位置.则图2中的值为 .
.16. 如图1,在中, , , , D是上一点,且 , 过点D作交于E,将绕A点顺时针旋转到图2的位置.则图2中的值为 .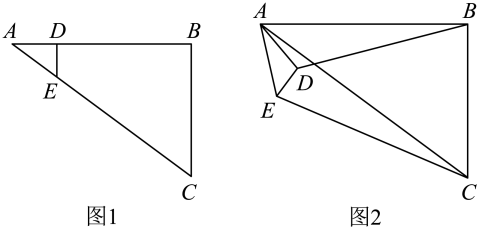
三、解答题
-
17. 如图,已知AB与CD相交于点O, , 求证: .

四、作图题
-
18. 如图,在中, .
 (1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.
(1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.五、综合题
-
19. 已知:如图,点M在的边上.

求作:射线 , 使 . 且点N在的平分线上.
作法:①以点O为圆心,适当长为半径画弧,分别交射线 , 于点C,D.
②分别以点C,D为圆心.大于长为半径画弧,两弧在的内部相交于点P.
③画射线 .
④以点M为圆心,长为半径画弧,交射线于点N.
⑤画射线 .
射线即为所求.
(1)、用尺规作图,依作法补全图形(保留作图痕迹);(2)、根据以上作图过程,完成下面的证明.证明:∵平分 .
∴ ,
∵ ,
∴ , ( ).(括号内填写推理依据)
∴ .
∴ . ( ).(填写推理依据)
20. 如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点 .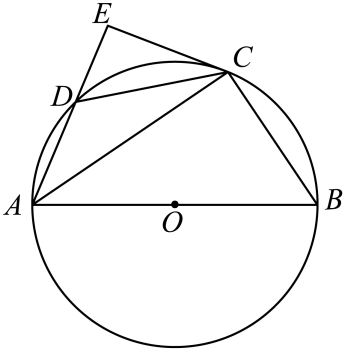 (1)、求证:是的切线;(2)、若 , , 求的长.21. 如图,在中, , AD平分交BC于点D,点E是斜边AC上一点,以AE为直径的经过点D,交AB于点F,连接DF.
(1)、求证:是的切线;(2)、若 , , 求的长.21. 如图,在中, , AD平分交BC于点D,点E是斜边AC上一点,以AE为直径的经过点D,交AB于点F,连接DF. (1)、求证:BC是的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).22. 如图, , 点是线段上的一点,且 . 已知 .
(1)、求证:BC是的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).22. 如图, , 点是线段上的一点,且 . 已知 .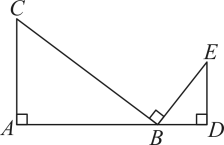 (1)、证明: .(2)、求线段的长.23. 如图,在中, , D是的中点,延长至E,连接 .
(1)、证明: .(2)、求线段的长.23. 如图,在中, , D是的中点,延长至E,连接 .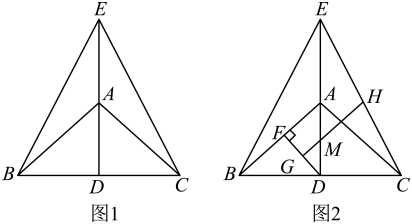 (1)、求证:;(2)、在如图1中,若 , 其它条件不变得到图2,在图2中过点D作于F,设H是的中点,过点H作交于G,交于M.
(1)、求证:;(2)、在如图1中,若 , 其它条件不变得到图2,在图2中过点D作于F,设H是的中点,过点H作交于G,交于M.求证:①;
② .
24. 已知:四边形为矩形, , , 点F是延长线上的一个动点(点F不与点C重合).连接交于点G. (1)、如图一,当点G为的中点时,求证:.(2)、如图二,过点C作 , 垂足为E.连接 , 设 , .求y关于x的函数关系式.(3)、如图三,在(2)的条件下,过点B作 , 交的延长线于点M.当时,求线段的长.25.
(1)、如图一,当点G为的中点时,求证:.(2)、如图二,过点C作 , 垂足为E.连接 , 设 , .求y关于x的函数关系式.(3)、如图三,在(2)的条件下,过点B作 , 交的延长线于点M.当时,求线段的长.25. (1)、如图 , 在中, , , 若的半径为 , 点在上,点在上,连接 , 求线段的最小值;(2)、如图所示,五边形是某市工业新区的外环路,新区管委会在点处,点处是该市的一个交通枢纽已知: , , 根据新区的自然环境及实际需求,现要在矩形区域内含边界修一个半径为的圆型环道;过圆心 , 作 , 垂足为 , 与交于点连接 , 点在上,连接其中,线段、及是要修的三条道路,要在所修迅路、之和最短的情况下,使所修道路最短,试求此时环道的圆心到的距离的长.
(1)、如图 , 在中, , , 若的半径为 , 点在上,点在上,连接 , 求线段的最小值;(2)、如图所示,五边形是某市工业新区的外环路,新区管委会在点处,点处是该市的一个交通枢纽已知: , , 根据新区的自然环境及实际需求,现要在矩形区域内含边界修一个半径为的圆型环道;过圆心 , 作 , 垂足为 , 与交于点连接 , 点在上,连接其中,线段、及是要修的三条道路,要在所修迅路、之和最短的情况下,使所修道路最短,试求此时环道的圆心到的距离的长.
-
-