2023年中考数学真题分类汇编(全国版):图形认识初步
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,中心对称图形是( ).A、
 B、
B、 C、
C、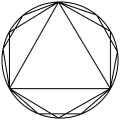 D、
D、 2. 下列图形中是棱锥的侧面展开图的是( )A、
2. 下列图形中是棱锥的侧面展开图的是( )A、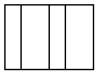 B、
B、 C、
C、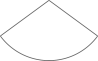 D、
D、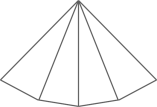 3. 如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
3. 如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
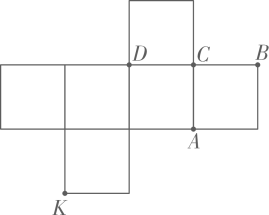 A、A点 B、B点 C、C点 D、D点4. 如图,直线AB,CD相交于点O,若 , , 则的度数为( )
A、A点 B、B点 C、C点 D、D点4. 如图,直线AB,CD相交于点O,若 , , 则的度数为( ) A、30° B、50° C、60° D、80°5. 将一副三角板按下图所示摆放在一组平行线内, , , 则的度数为( )
A、30° B、50° C、60° D、80°5. 将一副三角板按下图所示摆放在一组平行线内, , , 则的度数为( )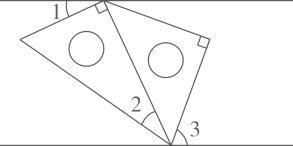 A、55° B、65° C、70° D、75°6. “争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( ).
A、55° B、65° C、70° D、75°6. “争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( ). A、文 B、明 C、典 D、范7. 如图,一束太阳光线平行照射在放置于地面的正六边形上,若 , 则的度数为( )
A、文 B、明 C、典 D、范7. 如图,一束太阳光线平行照射在放置于地面的正六边形上,若 , 则的度数为( ) A、 B、 C、 D、8. 如图1,汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就.其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”.为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线与地面所成夹角时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜与地面的夹角( )
A、 B、 C、 D、8. 如图1,汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就.其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”.为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线与地面所成夹角时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜与地面的夹角( ) A、 B、 C、 D、9. 下列图形中,是长方体表面展开图的是( )A、
A、 B、 C、 D、9. 下列图形中,是长方体表面展开图的是( )A、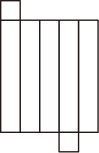 B、
B、 C、
C、 D、
D、
二、填空题
-
10. 如图,在数轴上, , 过作直线于点 , 在直线上截取 , 且在上方.连接 , 以点为圆心,为半径作弧交直线于点 , 则点的横坐标为 .
 11. 若直三棱柱的上下底面为正三角形,侧面展开图是边长为的正方形,则该直三棱柱的表面积为 .12. 一副三角板按如图所示放置,点A在上,点F在上,若 , 则°.
11. 若直三棱柱的上下底面为正三角形,侧面展开图是边长为的正方形,则该直三棱柱的表面积为 .12. 一副三角板按如图所示放置,点A在上,点F在上,若 , 则°.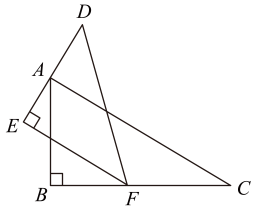 13. 如图,圆柱形玻璃杯的杯高为 , 底面周长为 , 在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿 , 且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为 . (杯壁厚度不计)
13. 如图,圆柱形玻璃杯的杯高为 , 底面周长为 , 在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿 , 且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为 . (杯壁厚度不计)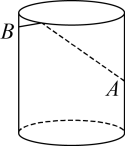
三、作图题
-
14.(1)、已知线段 , 求作 , 使得;(请用尺规作图,保留作图痕迹,不写作法.)
 (2)、求证:直角三角形斜边上的中线等于斜边的一半.(请借助上一小题所作图形,在完善的基础上,写出已知、求证与证明.)15. 1672年,丹麦数学家莫尔在他的著作《欧几里得作图》中指出:只用圆规可以完成一切尺规作图.1797年,意大利数学家马斯凯罗尼又独立发现此结论,并写在他的著作《圆规的几何学》中.请你利用数学家们发现的结论,完成下面的作图题:
(2)、求证:直角三角形斜边上的中线等于斜边的一半.(请借助上一小题所作图形,在完善的基础上,写出已知、求证与证明.)15. 1672年,丹麦数学家莫尔在他的著作《欧几里得作图》中指出:只用圆规可以完成一切尺规作图.1797年,意大利数学家马斯凯罗尼又独立发现此结论,并写在他的著作《圆规的几何学》中.请你利用数学家们发现的结论,完成下面的作图题:如图,已知 , 是上一点,只用圆规将的圆周四等分.(按如下步骤完成,保留作图痕迹)

①以点为圆心,长为半径,自点起,在上逆时针方向顺次截取;
②分别以点 , 点为圆心,长为半径作弧,两弧交于上方点;
③以点为圆心,长为半径作弧交于 , 两点.即点 , , , 将的圆周四等分.
四、综合题
-
16. 综合与实践
主题:制作无盖正方体形纸盒
素材:一张正方形纸板.
步骤1:如图1,将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图2,把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:
 (1)、直接写出纸板上与纸盒上的大小关系;(2)、证明(1)中你发现的结论.17. 某数学兴趣小组活动,准备将一张三角形纸片(如图)进行如下操作.并进行猜想和证明。
(1)、直接写出纸板上与纸盒上的大小关系;(2)、证明(1)中你发现的结论.17. 某数学兴趣小组活动,准备将一张三角形纸片(如图)进行如下操作.并进行猜想和证明。 (1)、用三角板分别取AB,AC的中点D,E,连结DE,画AF⊥DE于点F;(2)、用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无继隙无重叠).并用三角板画出示意图:(3)、请判断(2)中所拼的四边形的形状,并说明理由18. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点P到定点F(0,)的距离PF,始终等于它到定直线l:y=的距离PN (该结论不需要证明).他们称:定点F为图象的焦点,定直线l为图象的准线,y=叫做抛物线的准线方程.准线l与y轴的交点为H.其中原点O为FH的中点,FH=2OF= . 例如,抛物线y=2x2 , 其焦点坐标为F(0,),准线方程为l:y= , 其中PF=PN,FH=2OF= .
(1)、用三角板分别取AB,AC的中点D,E,连结DE,画AF⊥DE于点F;(2)、用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无继隙无重叠).并用三角板画出示意图:(3)、请判断(2)中所拼的四边形的形状,并说明理由18. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点P到定点F(0,)的距离PF,始终等于它到定直线l:y=的距离PN (该结论不需要证明).他们称:定点F为图象的焦点,定直线l为图象的准线,y=叫做抛物线的准线方程.准线l与y轴的交点为H.其中原点O为FH的中点,FH=2OF= . 例如,抛物线y=2x2 , 其焦点坐标为F(0,),准线方程为l:y= , 其中PF=PN,FH=2OF= . (1)、【基础训练】请分别直接写出抛物线y=的焦点坐标和准线l的方程: , ;(2)、【技能训练】如图2,已知抛物线y=上一点P(x0 , y0)(x0>0)到焦点F的距离是它到x轴距离的3倍,求点P的坐标;(3)、【能力提升】如图3,已知抛物线y=的焦点为F,准线方程为l.直线m:y=交y轴于点C,抛物线上动点P到x轴的距离为d1 , 到直线m的距离为d2 , 请直接写出d1+d2的最小值;(4)、【拓展延伸】该兴趣小组继续探究还发现:若将抛物线y=ax2(a>0)平移至y=a(x-h)2+k(a>0).
(1)、【基础训练】请分别直接写出抛物线y=的焦点坐标和准线l的方程: , ;(2)、【技能训练】如图2,已知抛物线y=上一点P(x0 , y0)(x0>0)到焦点F的距离是它到x轴距离的3倍,求点P的坐标;(3)、【能力提升】如图3,已知抛物线y=的焦点为F,准线方程为l.直线m:y=交y轴于点C,抛物线上动点P到x轴的距离为d1 , 到直线m的距离为d2 , 请直接写出d1+d2的最小值;(4)、【拓展延伸】该兴趣小组继续探究还发现:若将抛物线y=ax2(a>0)平移至y=a(x-h)2+k(a>0).抛物线y=a(x-h)2+k(a>0)内有一定点F(h,),直线l过点M(h,)且与x轴平行.当动点P在该抛物线上运动时,点P到直线l的距离PP1始终等于点P到点F的距离(该结论不需要证明).例如:抛物线y=2(x-1)2+3上的动点P到点F(1,)的距离等于点P到直线l:y=的距离.
请阅读上面的材料,探究下题:
如图4,点D(-1,)是第二象限内一定点,点P是抛物线y=-1上一动点.当PO+PD取最小值时,请求出△POD的面积.