2023年中考数学真题分类汇编（全国版）：二次函数（5）

试卷更新日期：2023-07-23 类型：二轮复习

进入出卷网下载

一、选择题

1. 如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $A (- 1 ， 0) 、 B (m ， 0)$ ，且 $1 < m < 2$ ，有下列结论：① $b < 0$ ；② $a + b > 0$ ；③ $0 < a < - c$ ；④若点 $C (- \frac{2}{3} ， y_{1}) ， D (\frac{5}{3} ， y_{2})$ 在抛物线上，则 $y_{1} > y_{2}$ ．其中，正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 已知二次函数 $y = a x^{2} - (3 a + 1) x + 3 (a \neq 0)$ ，下列说法正确的是（）

A、点 $(1 ， 2)$ 在该函数的图象上 B、当 $a = 1$ 且 $- 1 \leq x \leq 3$ 时， $0 \leq y \leq 8$ C、该函数的图象与x轴一定有交点 D、当 $a > 0$ 时，该函数图象的对称轴一定在直线 $x = \frac{3}{2}$ 的左侧

查看试题解析
3. 如图，二次函数 $y = a x^{2} + x - 6$ 的图象与x轴交于 $A (- 3 ， 0)$ ， B两点，下列说法正确的是（）

A、抛物线的对称轴为直线 $x = 1$ B、抛物线的顶点坐标为 $(- \frac{1}{2} ， - 6)$ C、A，B两点之间的距离为5 D、当 $x < - 1$ 时，y的值随x值的增大而增大

查看试题解析
4. 已知二次函数 $y = a x^{2} - 2 a x + 3$ （其中 $x$ 是自变量），当 $0 < x < 3$ 时对应的函数值 $y$ 均为正数，则 $a$ 的取值范围为（）

A、 $0 < a < 1$ B、 $a < - 1$ 或 $a > 3$ C、 $- 3 < a < 0$ 或 $0 < a < 3$ D、 $- 1 < a < 0$ 或 $0 < a < 3$

查看试题解析
5. 经过 $A (2 - 3 b ， m) ， B (4 b + c - 1 ， m)$ 两点的抛物线 $y = - \frac{1}{2} x^{2} + b x - b^{2} + 2 c$ （ $x$ 为自变量）与 $x$ 轴有交点，则线段 $A B$ 长为（）

A、10 B、12 C、13 D、15

查看试题解析
6. 一个球从地面竖直向上弹起时的速度为10米/秒，经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t² ，那么球弹起后又回到地面所花的时间t(秒)是（）

A、5 B、10 C、1 D、2

查看试题解析
7. 如图，拋物线 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 为常数）关于直线 $x = 1$ 对称．下列五个结论：① $a b c > 0$ ；② $2 a + b = 0$ ；③ $4 a + 2 b + c > 0$ ；④ $a m^{2} + b m > a + b$ ；⑤ $3 a + c > 0$ ．其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，则下列结论中正确的是（）

A、 $a b c < 0$ B、 $4 a - 2 b + c < 0$ C、 $3 a + c = 0$ D、 $a m^{2} + b m + a \leq 0$ （ $m$ 为实数）

查看试题解析

二、填空题

9. 定义：若x，y满足 $x^{2} = 4 y + t ， y^{2} = 4 x + t$ 且 $x \neq y$ （t为常数），则称点 $M (x ， y)$ 为“和谐点”．

(1)、若 $P (3 ， m)$ 是“和谐点”，则 $m =$ ．

(2)、若双曲线 $y = \frac{k}{x} (- 3 < x < - 1)$ 存在“和谐点”，则k的取值范围为．

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $A (- 3 ， 0)$ ，顶点为 $M (- 1 ， m)$ ，且抛物线与 $y$ 轴的交点B在 $(0 ， - 2)$ 和 $(0 ， - 3)$ 之间（不含端点），则下列结论：

①当 $- 3 \leq x \leq 1$ 时， $y \leq 1$ ；

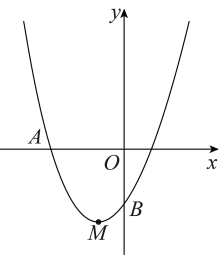
②当 $△ A B M$ 的面积为 $\frac{3 \sqrt{3}}{2}$ 时， $a = \frac{\sqrt{3}}{2}$ ；

③当 $△ A B M$ 为直角三角形时，在 $△ A O B$ 内存在唯一点P，使得 $P A + P O + P B$ 的值最小，最小值的平方为 $18 + 9 \sqrt{3}$ ．

其中正确的结论是．（填写所有正确结论的序号）

查看试题解析

三、综合题

11. 某工厂计划从A，B两种产品中选择一种生产并销售，每日产销x件．已知A产品成本价m元/件（m为常数，且 $4 \leq m \leq 6$ ，售价8元/件，每日最多产销500件，同时每日共支付专利费30元；B产品成本价12元/件，售价20元/件，每日最多产销300件，同时每日支付专利费y元，y（元）与每日产销x（件）满足关系式 $y = 80 + 0.01 x^{2 .}$

(1)、若产销A，B两种产品的日利润分别为 $w_{1}$ 元， $w_{2}$ 元，请分别写出 $w_{1}$ ， $w_{2}$ 与x的函数关系式，并写出x的取值范围；

(2)、分别求出产销A，B两种产品的最大日利润．（A产品的最大日利润用含m的代数式表示）

(3)、为获得最大日利润，该工厂应该选择产销哪种产品？并说明理由．【利润 $=$ （售价 $-$ 成本） $\times$ 产销数量 $-$ 专利费】

查看试题解析
12. 一次足球训练中，小明从球门正前方8m的 $A$ 处射门，球射向球门的路线呈抛物线.当球飞行的水平距离为6m时，球达到最高点，此时球离地面3m.已知球门高OB为2.44m，现以 $O$ 为原点建立如图所示直角坐标系.

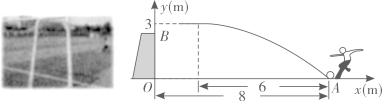(1)、求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）。

(2)、对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点 $O$ 正上方2.25m处?

查看试题解析
13. 已知二次函数 $y = - x^{2} + b x + c$ .

(1)、当 $b = 4 ， c = 3$ 时，
①求该函数图象的顶点坐标.
②当 $- 1 ⩽ x ⩽ 3$ 时，求 $y$ 的取值范围.

(2)、当 $x ⩽ 0$ 时， $y$ 的最大值为2；当 $x > 0$ 时， $y$ 的最大值为3，求二次函数的表达式.

查看试题解析
14. 如图，已知二次函数 $y = x^{2} + b x + c$ 图象经过点 $A (1 ， - 2)$ 和 $B (0 ， - 5)$ ．

(1)、求该二次函数的表达式及图象的顶点坐标．

(2)、当 $y \leq - 2$ 时，请根据图象直接写出x的取值范围．

查看试题解析
15. 在二次函数 $y = x^{2} - 2 t x + 3 (t > 0)$ 中，

(1)、若它的图象过点 $(2 ， 1)$ ，则t的值为多少？

(2)、当 $0 \leq x \leq 3$ 时，y的最小值为 $- 2$ ，求出t的值：

(3)、如果 $A (m - 2 ， a) ， B (4 ， b) ， C (m ， a)$ 都在这个二次函数的图象上，且 $a < b < 3$ ，求m的取值范围。

查看试题解析
16. 已知点(-m，0)和(3m，0)在二次函数y=ax²+bx+3(a，b是常数，a≠0)的图象上。

(1)、当m=-1时，求a和b的值：

(2)、若二次函数的图象经过点A(n，3)且点A不在坐标轴上，当-2<m<-1时，求n的取值范围：

(3)、求证：b²+4a=0．

查看试题解析
17. 如图1，抛物线 $y = a x^{2} + b x + 3$ （ $a \neq 0$ ）与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ．

(1)、求抛物线的解析式；

(2)、点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；

(3)、如图2，抛物线顶点为D，对称轴与x轴交于点E，过点 $K (1 ， 3)$ 的直线（直线 $K D$ 除外）与抛物线交于G，H两点，直线 $D G$ ， $D H$ 分别交x轴于点M，N．试探究 $E M \cdot E N$ 是否为定值，若是，求出该定值；若不是，说明理由．

查看试题解析
18. 在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x + c$ 与x轴交于点 $A (- 3 ， 0) ， B (1 ， 0)$ 两点，与y轴交于点 $C (0 ， 3)$ ，点P是抛物线上的一个动点．

(1)、求抛物线的表达式；

(2)、当点P在直线 $A C$ 上方的抛物线上时，连接 $B P$ 交 $A C$ 于点D．如图1．当 $\frac{P D}{D B}$ 的值最大时，求点P的坐标及 $\frac{P D}{D B}$ 的最大值；

(3)、过点P作x轴的垂线交直线 $A C$ 于点M，连接 $P C$ ，将 $△ P C M$ 沿直线 $P C$ 翻折，当点M的对应点 $M'$ 恰好落在y轴上时，请直接写出此时点M的坐标．

查看试题解析
19. 在平面直角坐标系中， $O$ 为坐标原点，抛物线 $y = \frac{1}{4} x^{2} + b x + c$ 经过点 $O (0$ ， $0)$ ，对称轴过点 $B (2$ ， $0)$ ，直线 $l$ 过点 $C (2 ， - 2)$ ，且垂直于 $y$ 轴．过点 $B$ 的直线 $l_{1}$ 交抛物线于点 $M$ 、 $N$ ，交直线 $l$ 于点 $Q$ ，其中点 $M$ 、Q在抛物线对称轴的左侧．
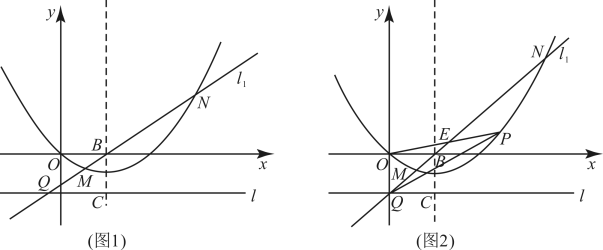(1)求抛物线的解析式；

(1)、如图1，当 $B M ： M Q = 3 ： 5$ 时，求点 $N$ 的坐标；

(2)、如图2，当点 $Q$ 恰好在 $y$ 轴上时， $P$ 为直线 $l_{1}$ 下方的抛物线上一动点，连接 $P Q$ 、 $P O$ ，其中 $P O$ 交 $l_{1}$ 于点 $E$ ，设 $△ O Q E$ 的面积为 $S_{1}$ ， $△ P Q E$ 的面积为 $S_{2}$ ．求 $\frac{S_{2}}{S_{1}}$ 的最大值．

查看试题解析
20. 已知 $(x_{1} ， y_{1}) ， (x_{2} ， y_{2})$ 是抛物 $C_{1} ： y = - \frac{1}{4} x^{2} + b x$ （b为常数）上的两点，当 $x_{1} + x_{2} = 0$ 时，总有 $y_{1} = y_{2}$

(1)、求b的值；

(2)、将抛物线 $C_{1}$ 平移后得到抛物线 $C_{2} ： y = - \frac{1}{4} (x - m)^{2} + 1 (m > 0)$ ．
探究下列问题：

①若抛物线 $C_{1}$ 与抛物线 $C_{2}$ 有一个交点，求m的取值范围；

②设抛物线C₂与x轴交于A，B两点，与y轴交于点C，抛物线 $C_{2}$ 的顶点为点E， $△ A B C$ 外接圆的圆心为点F，如果对抛物线 $C_{1}$ 上的任意一点P，在抛物线 $C_{2}$ 上总存在一点Q，使得点P、Q的纵坐标相等．求EF长的取值范围．

查看试题解析
21. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于点 $A (- 4 ， 0)$ 、 $B (2 ， 0)$ ，且经过点 $C (- 2 ， 6)$ ．

(1)、求抛物线的表达式；

(2)、在x轴上方的抛物线上任取一点N，射线 $A N$ 、 $B N$ 分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为 $Q^{'}$ ，求 $△ A P Q^{'}$ 的面积；

(3)、点M是y轴上一动点，当 $∠ A M C$ 最大时，求M的坐标．

查看试题解析
22. 如图，在平面直角坐标系 $x O y$ 中，拋物线 $L_{1} ： y = x^{2} - 2 x - 3$ 的顶点为 $P$ .直线 $l$ 过点 $M (0 ， m) (m ⩾ - 3)$ ，且平行于 $x$ 轴，与拖物线 $L_{1}$ 交于 $A 、 B$ （ $B$ 在 $A$ 的右侧）.将抛物线 $L_{1}$ 沿直线 $l$ 翻折得到抛物线 $L_{2}$ ，抛物线 $L_{2}$ 交 $y$ 轴于点 $C$ ，顶点为 $D$ .

(1)、当 $m = 1$ 时，求点 $D$ 的坐标；

(2)、连接 $B C 、 C D 、 D B$ ，若 $△ B C D$ 为直角三角形，求此时 $L_{2}$ 所对应的函数表达式；

(3)、在（2）的条件下，若 $△ B C D$ 的面积为3， $E 、 F$ 两点分别在边 $B C 、 C D$ 上运动，且 $E F = C D$ ，以 $E F$ 为一边作正方形 $E F G H$ ，连接 $C G$ ，写出 $C G$ 长度的最小值，并简要说明理由.

查看试题解析
23. 如图，直线 $y = \frac{\sqrt{5}}{2} x + \sqrt{5}$ 与 $x$ 轴， $y$ 轴分别交于点A，B，抛物线的顶点 $P$ 在直线AB上，与 $x$ 轴的交点为C，D，其中点 $C$ 的坐标为 $(2 ， 0)$ .直线BC与直线PD相交于点 $E$ .

(1)、如图2，若抛物线经过原点 $O$ .
①求该抛物线的函数表达式；②求 $\frac{B E}{E C}$ 的值.

(2)、连结 $P C ， ∠ C P E$ 与 $∠ B A O$ 能否相等？若能，求符合条件的点 $P$ 的横坐标；若不能，试说明理由.

查看试题解析
24. 如图，在平面直角坐标系xOy中，已知抛物线 $y = a x^{2} + c$ 经过点 $P (4 ， - 3)$ ，与y轴交于点 $A (0 ， 1)$ ，直线 $y = k x (k \neq 0)$ 与抛物线交于B，C两点.

(1)、求抛物线的函数表达式；

(2)、若 $△ A B P$ 是以AB为腰的等腰三角形，求点B的坐标；

(3)、过点 $M (0 ， m)$ 作y轴的垂线，交直线AB于点D，交直线AC于点E. 试探究：是否存在常数m，使得 $O D ⊥ O E$ 始终成立？若存在，求出m的值；若不存在，请说明理由.

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x + c$ 过点 $A (- 1 ， 0) ， B (3 ， 0) ， C (0 ， 3)$ ．

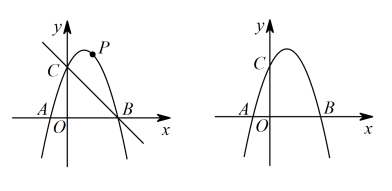(1)、求抛物线的解析式；

(2)、设点 $P$ 是直线 $B C$ 上方抛物线上一点，求出 $△ P B C$ 的最大面积及此时点 $P$ 的坐标；

(3)、若点 $M$ 是抛物线对称轴上一动点，点 $N$ 为坐标平面内一点，是否存在以 $B C$ 为边，点 $B 、 C 、 M 、 N$ 为顶点的四边形是菱形，若存在，请直接写出点 $N$ 的坐标；若不存在，请说明理由．

查看试题解析
26. 如图，已知抛物线与 $x$ 轴交于 $A (1 ， 0)$ 和 $B (- 5 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ．直线 $y = - 3 x + 3$ 过抛物线的顶点 $P$ ．

(1)、求抛物线的函数解析式；

(2)、若直线 $x = m (- 5 < m < 0)$ 与抛物线交于点 $E$ ，与直线 $B C$ 交于点 $F$ ．
①当 $E F$ 取得最大值时，求 $m$ 的值和 $E F$ 的最大值；

②当 $△ E F C$ 是等腰三角形时，求点 $E$ 的坐标．

查看试题解析
27. 如图，在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} + 2 x + c$ 与坐标轴分别相交于点A，B， $C (0 ， 6)$ 三点，其对称轴为 $x = 2$ ．

(1)、求该抛物线的解析式；

(2)、点 $F$ 是该抛物线上位于第一象限的一个动点，直线 $A F$ 分别与 $y$ 轴，直线 $B C$ 交于点 $D$ ， $E$ ．
①当 $C D = C E$ 时，求 $C D$ 的长；
②若 $△ C A D$ ， $△ C D E$ ， $△ C E F$ 的面积分别为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ，且满足 $S_{1} + S_{3} = 2 S_{2}$ ，求点 $F$ 的坐标．

查看试题解析
28. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 2$ 过点 $(1 ， 3)$ ，且交x轴于点 $A (- 1 ， 0)$ ， B两点，交y轴于点C．

(1)、求抛物线的表达式；

(2)、点P是直线 $B C$ 上方抛物线上的一动点，过点P作 $P D ⊥ B C$ 于点D，过点P作y轴的平行线交直线 $B C$ 于点E，求 $△ P D E$ 周长的最大值及此时点P的坐标；

(3)、在（2）中 $△ P D E$ 周长取得最大值的条件下，将该抛物线沿射线 $C B$ 方向平移 $\sqrt{5}$ 个单位长度，点M为平移后的抛物线的对称轴上一点．在平面内确定一点N，使得以点A，P，M，N为顶点的四边形是菱形，写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．

查看试题解析
29. 如图，在平面直角坐标系中，抛物线 $y = \frac{1}{4} x^{2} + b x + c$ 与 $x$ 轴交于点 $A$ ， $B$ ，与 $y$ 轴交于点 $C$ ，其中 $B (3 ， 0)$ ， $C (0 ， - 3)$ ．

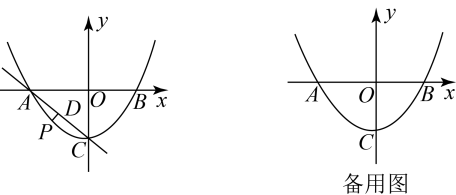(1)、求该抛物线的表达式；

(2)、点 $P$ 是直线 $A C$ 下方抛物线上一动点，过点 $P$ 作 $P D ⊥ A C$ 于点 $D$ ，求 $P D$ 的最大值及此时点 $P$ 的坐标；

(3)、在（2）的条件下，将该抛物线向右平移 $5$ 个单位，点 $E$ 为点 $P$ 的对应点，平移后的抛物线与 $y$ 轴交于点 $F$ ， $Q$ 为平移后的抛物线的对称轴上任意一点．写出所有使得以 $Q F$ 为腰的 $△ Q E F$ 是等腰三角形的点 $Q$ 的坐标，并把求其中一个点 $Q$ 的坐标的过程写出来．

查看试题解析