2023年中考数学真题分类汇编(全国版):二次函数(4)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 已知抛物线 , 则当时,函数的最大值为( )A、 B、 C、0 D、22. 抛物线与x轴的一个交点为 , 若 , 则实数的取值范围是( )A、 B、或 C、 D、或3. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限4. 已知二次函数(a为常数,且),下列结论:
①函数图象一定经过第一、二、四象限;②函数图象一定不经过第三象限;③当时,y随x的增大而减小;④当时,y随x的增大而增大.
其中所有正确结论的序号是( )A、①② B、②③ C、② D、③④5. 如图所示,二次函数为常数,的图象与轴交于点 . 有下列结论:①;②若点和均在抛物线上,则;③;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个6. 如图,二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列四个结论:①;②;③;④当时,;其中正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个6. 如图,二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列四个结论:①;②;③;④当时,;其中正确结论的个数为( ) A、1个 B、2个 C、3个 D、4个7. 已知点在同一个函数图象上,则这个函数图象可能是( )A、
A、1个 B、2个 C、3个 D、4个7. 已知点在同一个函数图象上,则这个函数图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 已知二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列论中:①;②若点均在该二次函数图象上,则;③若m为任意实数,则;④方程的两实数根为 , 且 , 则 . 正确结论的序号为( )A、①②③ B、①③④ C、②③④ D、①④9. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:
8. 已知二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列论中:①;②若点均在该二次函数图象上,则;③若m为任意实数,则;④方程的两实数根为 , 且 , 则 . 正确结论的序号为( )A、①②③ B、①③④ C、②③④ D、①④9. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为 .
其中,正确结论的个数是( )
 A、0 B、1 C、2 D、310. 抛物线的图象如图所示,对称轴为直线 . 下列说法:①;②;③(t为全体实数);④若图象上存在点和点 , 当时,满足 , 则m的取值范围为 . 其中正确的个数有( )
A、0 B、1 C、2 D、310. 抛物线的图象如图所示,对称轴为直线 . 下列说法:①;②;③(t为全体实数);④若图象上存在点和点 , 当时,满足 , 则m的取值范围为 . 其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的距离m.
 12. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形 , 则.
12. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形 , 则.
三、综合题
-
13. 某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离(单位:)以、飞行高度(单位:)随飞行时间(单位:)变化的数据如下表.
飞行时间
0
2
4
6
8
…
飞行水平距离
0
10
20
30
40
…
飞行高度
0
22
40
54
64
…
探究发现:与 , 与之间的数量关系可以用我们已学过的函数来描述.直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围).
问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
 (1)、若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;(2)、在安全线上设置回收区域 . 若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.14. 设二次函数 , ( , 是实数).已知函数值和自变量的部分对应取值如下表所示:
(1)、若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;(2)、在安全线上设置回收区域 . 若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.14. 设二次函数 , ( , 是实数).已知函数值和自变量的部分对应取值如下表所示:…
0
1
2
3
…
…
1
1
…
(1)、若 , 求二次函数的表达式;(2)、写出一个符合条件的的取值范围,使得随的增大而减小.(3)、若在m、n、p这三个实数中,只有一个是正数,求的取值范围.15. 抛物线交轴于两点(在的左边),交轴于点 .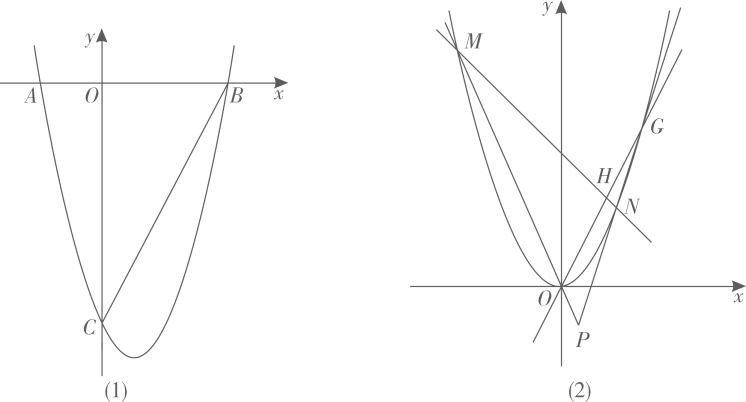 (1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.16. 如图,已知 . 点E位于第二象限且在直线上, , , 连接 .
(1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.16. 如图,已知 . 点E位于第二象限且在直线上, , , 连接 . (1)、直接判断的形状:是三角形;(2)、求证:;(3)、直线EA交x轴于点 . 将经过B,C两点的抛物线向左平移2个单位,得到抛物线 .
(1)、直接判断的形状:是三角形;(2)、求证:;(3)、直线EA交x轴于点 . 将经过B,C两点的抛物线向左平移2个单位,得到抛物线 .①若直线与抛物线有唯一交点,求t的值;
②若抛物线的顶点P在直线上,求t的值;
③将抛物线再向下平移,个单位,得到抛物线 . 若点D在抛物线上,求点D的坐标.
17. (1)、【建立模型】如图 , 点是线段上的一点, , , , 垂足分别为 , , , . 求证:;(2)、 【类比迁移】如图 , 一次函数的图象与轴交于点、与轴交于点 , 将线段绕点逆时针旋转得到、直线交轴于点 .
(1)、【建立模型】如图 , 点是线段上的一点, , , , 垂足分别为 , , , . 求证:;(2)、 【类比迁移】如图 , 一次函数的图象与轴交于点、与轴交于点 , 将线段绕点逆时针旋转得到、直线交轴于点 .①求点的坐标;
②求直线的解析式;
(3)、【拓展延伸】如图 , 抛物线与轴交于 , 两点点在点的左侧 , 与轴交于点,已知点 , , 连接 . 抛物线上是否存在点 , 使得 , 若存在,求出点的横坐标.18. 如图,抛物线经过两点,并交x轴于另一点B,点M是抛物线的顶点,直线AM与轴交于点D. (1)、求该抛物线的表达式;(2)、若点H是x轴上一动点,分别连接MH,DH,求的最小值;(3)、若点P是抛物线上一动点,问在对称轴上是否存在点Q,使得以D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.19. 如图,已知抛物线与x轴交于点和点B,与y轴交于点C,连接 , 过B、C两点作直线.
(1)、求该抛物线的表达式;(2)、若点H是x轴上一动点,分别连接MH,DH,求的最小值;(3)、若点P是抛物线上一动点,问在对称轴上是否存在点Q,使得以D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.19. 如图,已知抛物线与x轴交于点和点B,与y轴交于点C,连接 , 过B、C两点作直线. (1)、求a的值.(2)、将直线向下平移个单位长度,交抛物线于、两点.在直线上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线的距离最大,若存在,请求出点D的坐标;若不存在,请说明理由.(3)、抛物线上是否存在点P,使 , 若存在,请求出直线的解析式;若不存在,请说明理由.20. 如图一所示,在平面直角坐标系中,抛物线与轴交于两点,与轴交于点 .
(1)、求a的值.(2)、将直线向下平移个单位长度,交抛物线于、两点.在直线上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线的距离最大,若存在,请求出点D的坐标;若不存在,请说明理由.(3)、抛物线上是否存在点P,使 , 若存在,请求出直线的解析式;若不存在,请说明理由.20. 如图一所示,在平面直角坐标系中,抛物线与轴交于两点,与轴交于点 . (1)、求抛物线的函数表达式及顶点坐标;(2)、点为第三象限内抛物线上一点,作直线 , 连接、 , 求面积的最大值及此时点的坐标;(3)、设直线交抛物线于点、 , 求证:无论为何值,平行于轴的直线上总存在一点 , 使得为直角.21. 如图,抛物线与轴交于两点,与轴交于点 . 抛物线的对称轴与经过点的直线交于点 , 与轴交于点 .
(1)、求抛物线的函数表达式及顶点坐标;(2)、点为第三象限内抛物线上一点,作直线 , 连接、 , 求面积的最大值及此时点的坐标;(3)、设直线交抛物线于点、 , 求证:无论为何值,平行于轴的直线上总存在一点 , 使得为直角.21. 如图,抛物线与轴交于两点,与轴交于点 . 抛物线的对称轴与经过点的直线交于点 , 与轴交于点 .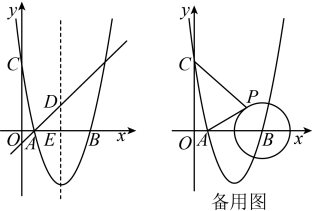 (1)、求直线及抛物线的表达式;(2)、在抛物线上是否存在点 , 使得是以为直角边的直角三角形?若存在,求出所有点的坐标;若不存在,请说明理由;(3)、以点为圆心,画半径为2的圆,点为上一个动点,请求出的最小值.22. 如图1,抛物线与轴交于点 , 与直线交于点 , 点在轴上.点从点出发,沿线段方向匀速运动,运动到点时停止.
(1)、求直线及抛物线的表达式;(2)、在抛物线上是否存在点 , 使得是以为直角边的直角三角形?若存在,求出所有点的坐标;若不存在,请说明理由;(3)、以点为圆心,画半径为2的圆,点为上一个动点,请求出的最小值.22. 如图1,抛物线与轴交于点 , 与直线交于点 , 点在轴上.点从点出发,沿线段方向匀速运动,运动到点时停止. (1)、求抛物线的表达式;(2)、当时,请在图1中过点作交抛物线于点 , 连接 , , 判断四边形的形状,并说明理由.(3)、如图2,点从点开始运动时,点从点同时出发,以与点相同的速度沿轴正方向匀速运动,点停止运动时点也停止运动.连接 , , 求的最小值.23. 如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接 , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 .
(1)、求抛物线的表达式;(2)、当时,请在图1中过点作交抛物线于点 , 连接 , , 判断四边形的形状,并说明理由.(3)、如图2,点从点开始运动时,点从点同时出发,以与点相同的速度沿轴正方向匀速运动,点停止运动时点也停止运动.连接 , , 求的最小值.23. 如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接 , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 .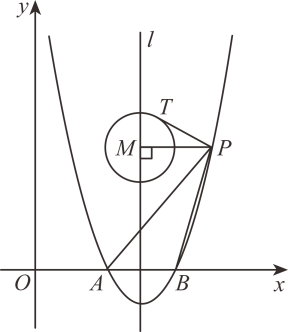 (1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.24. 已知抛物线 , 为常数,的顶点为 , 与轴相交于 , 两点点在点的左侧 , 与轴相交于点 , 抛物线上的点的横坐标为 , 且 , 过点作 , 垂足为 .(1)、若 .
(1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.24. 已知抛物线 , 为常数,的顶点为 , 与轴相交于 , 两点点在点的左侧 , 与轴相交于点 , 抛物线上的点的横坐标为 , 且 , 过点作 , 垂足为 .(1)、若 .①求点和点的坐标;
②当时,求点的坐标;
(2)、若点的坐标为 , 且 , 当时,求点的坐标.25. 在平面直角坐标系中,已知点A在y轴正半轴上. (1)、如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.
(1)、如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.① ▲ ;
②如图1,已知菱形的顶点B、C、D在该二次函数的图象上,且轴,求菱形的边长;
③如图2,已知正方形的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究是否为定值.如果是,求出这个值;如果不是,请说明理由.
(2)、已知正方形的顶点B、D在二次函数(a为常数,且)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.26. 如图,二次函数的图象交轴于点 , 交轴于点 , 点的坐标为 , 对称轴是直线 , 点是轴上一动点,轴,交直线于点 , 交抛物线于点 . (1)、求这个二次函数的解析式.(2)、若点在线段上运动(点与点、点不重合),求四边形面积的最大值,并求出此时点的坐标.(3)、若点在轴上运动,则在轴上是否存在点 , 使以、为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
(1)、求这个二次函数的解析式.(2)、若点在线段上运动(点与点、点不重合),求四边形面积的最大值,并求出此时点的坐标.(3)、若点在轴上运动,则在轴上是否存在点 , 使以、为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.