2023年中考数学真题分类汇编(全国版):二次函数(3)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 已知 , 若关于x的方程的解为 . 关于x的方程的解为 . 则下列结论正确的是( )A、 B、 C、 D、2. 已知点在直线上,点在抛物线上,若且 , 则的取值范围是( )A、 B、 C、 D、3. 已知抛物线( , , 是常数且)过和两点,且 , 下列四个结论:;;若抛物线过点 , 则;关于的方程有实数根,则其中正确的结论有( )A、1个 B、2个 C、3个 D、4个4. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线 . 则下列结论正确的有( )
①;
②;
③方程的两个根为;
④抛物线上有两点和 , 若且 , 则 .
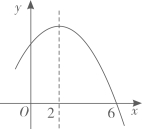 A、1个 B、2个 C、3个 D、4个5. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为6. 如图,抛物线的顶点的坐标为 , 与轴的一个交点位于0合和1之间,则以下结论:①;②;③若图象经过点 , 则;④若关于的一元二次方程无实数根,则 . 其中正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个5. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为6. 如图,抛物线的顶点的坐标为 , 与轴的一个交点位于0合和1之间,则以下结论:①;②;③若图象经过点 , 则;④若关于的一元二次方程无实数根,则 . 其中正确结论的个数是( )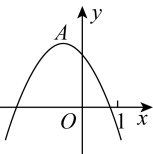 A、1 B、2 C、3 D、47. 如图,在平面直角坐标系中,直线与抛物线相交于点 , . 结合图象,判断下列结论:①当时,;②是方程的一个解;③若 , 是抛物线上的两点,则;④对于抛物线, , 当时,的取值范围是 . 其中正确结论的个数是( )
A、1 B、2 C、3 D、47. 如图,在平面直角坐标系中,直线与抛物线相交于点 , . 结合图象,判断下列结论:①当时,;②是方程的一个解;③若 , 是抛物线上的两点,则;④对于抛物线, , 当时,的取值范围是 . 其中正确结论的个数是( ) A、4个 B、3个 C、2个 D、1个8. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( )
A、4个 B、3个 C、2个 D、1个8. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
9. 要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为 , 水柱落地处离池中心 , 水管长度应为 .
 10. 已知抛物线经过两点,若分别位于抛物线对称轴的两侧,且 , 则的取值范围是 .11. 抛物线(是常数,)经过三点,且 . 下列四个结论:
10. 已知抛物线经过两点,若分别位于抛物线对称轴的两侧,且 , 则的取值范围是 .11. 抛物线(是常数,)经过三点,且 . 下列四个结论:①;
②;
③当时,若点在该抛物线上,则;
④若关于的一元二次方程有两个相等的实数根,则 .
其中正确的是(填写序号).
三、解答题
-
12. 如图,抛物线与x轴交于 , 两点,与轴交于点 .
 (1)、求抛物线解析式及 , 两点坐标;(2)、以 , , , 为顶点的四边形是平行四边形,求点坐标;(3)、该抛物线对称轴上是否存在点 , 使得 , 若存在,求出点的坐标;若不存在,请说明理由.
(1)、求抛物线解析式及 , 两点坐标;(2)、以 , , , 为顶点的四边形是平行四边形,求点坐标;(3)、该抛物线对称轴上是否存在点 , 使得 , 若存在,求出点的坐标;若不存在,请说明理由.四、综合题
-
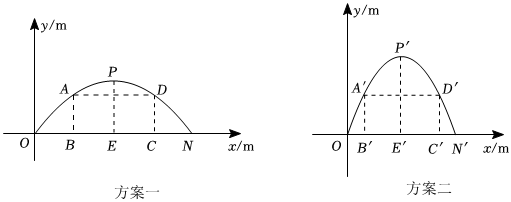
13. 某校想将新建图书楼的正门设计为一个抛物线型门,并要求所设计的拱门的跨度与拱高之积为 , 还要兼顾美观、大方,和谐、通畅等因素,设计部门按要求价出了两个设计方案现把这两个方案中的拱门图形放入平面直角坐标系中,如图所示:
方案一,抛物线型拱门的跨度 , 拱高其中,点在轴上, , .
方案二,抛物线型拱门的跨度 , 拱高其中,点在轴上, , .
要在拱门中设置高为的矩形框架,其面积越大越好框架的粗细忽略不计方案一中,矩形框架的面积记为 , 点、在抛物线上,边在上;方案二中,矩形框架的面积记为 , 点 , 在抛物线上,边在上现知,小华已正确求出方案二中,当时, , 请你根据以上提供的相关信息,解答下列问题:
 (1)、求方案一中抛物线的函数表达式;(2)、在方案一中,当时,求矩形框架的面积并比较 , 的大小.14. “端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.(1)、当时,;(2)、当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?(3)、小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为 . ”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.15. 为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为 , 已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元(1)、 , ;(2)、求第x天的销售额W元与x之间的函数关系式;(3)、在试销售的30天中,销售额超过1000元的共有多少天?16. 已知:y关于x的函数 .
(1)、求方案一中抛物线的函数表达式;(2)、在方案一中,当时,求矩形框架的面积并比较 , 的大小.14. “端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.(1)、当时,;(2)、当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?(3)、小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为 . ”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.15. 为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为 , 已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元(1)、 , ;(2)、求第x天的销售额W元与x之间的函数关系式;(3)、在试销售的30天中,销售额超过1000元的共有多少天?16. 已知:y关于x的函数 . (1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .
(1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,-是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
17. 如图①,抛物线与x轴交于点 , , 与y轴交于点C,连接AC,BC.点P是x轴上任意一点. (1)、求抛物线的表达式;(2)、点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;(3)、如图②,当点从点A出发沿x轴向点B运动时(点P与点A,B不重合),自点P分别作 , 交AC于点E,作 , 垂足为点D.当m为何值时,面积最大,并求出最大值.18. 已知抛物线与轴相交于点 , , 与轴相交于点 .
(1)、求抛物线的表达式;(2)、点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;(3)、如图②,当点从点A出发沿x轴向点B运动时(点P与点A,B不重合),自点P分别作 , 交AC于点E,作 , 垂足为点D.当m为何值时,面积最大,并求出最大值.18. 已知抛物线与轴相交于点 , , 与轴相交于点 . (1)、求抛物线的表达式;(2)、如图1,点是抛物线的对称轴上的一个动点,当的周长最小时,求的值;(3)、如图2,取线段的中点 , 在抛物线上是否存在点 , 使?若存在,求出点的坐标;若不存在,请说明理由.19. 如图,在平面直角坐标系中,菱形的一边在轴正半轴上,顶点的坐标为 , 点是边上的动点,过点作交边于点 , 作交边于点 , 连接 . 设的面积为 .
(1)、求抛物线的表达式;(2)、如图1,点是抛物线的对称轴上的一个动点,当的周长最小时,求的值;(3)、如图2,取线段的中点 , 在抛物线上是否存在点 , 使?若存在,求出点的坐标;若不存在,请说明理由.19. 如图,在平面直角坐标系中,菱形的一边在轴正半轴上,顶点的坐标为 , 点是边上的动点,过点作交边于点 , 作交边于点 , 连接 . 设的面积为 . (1)、求关于的函数解析式;(2)、当取何值时,的值最大?请求出最大值.20. 如图,在平面直角坐标系中,抛物线经过点和点 , 且与直线交于两点(点在点的右侧),点为直线上的一动点,设点的横坐标为 .
(1)、求关于的函数解析式;(2)、当取何值时,的值最大?请求出最大值.20. 如图,在平面直角坐标系中,抛物线经过点和点 , 且与直线交于两点(点在点的右侧),点为直线上的一动点,设点的横坐标为 . (1)、求抛物线的解析式.(2)、过点作轴的垂线,与拋物线交于点 . 若 , 求面积的最大值.(3)、抛物线与轴交于点 , 点为平面直角坐标系上一点,若以为顶点的四边形是菱形,请求出所有满足条件的点的坐标.21. 已知二次函数 .(1)、若 , 且该二次函数的图象过点 , 求的值;(2)、如图所示,在平面直角坐标系中,该二次函数的图象与轴交于点 , 且 , 点D在上且在第二象限内,点在轴正半轴上,连接 , 且线段交轴正半轴于点 , .
(1)、求抛物线的解析式.(2)、过点作轴的垂线,与拋物线交于点 . 若 , 求面积的最大值.(3)、抛物线与轴交于点 , 点为平面直角坐标系上一点,若以为顶点的四边形是菱形,请求出所有满足条件的点的坐标.21. 已知二次函数 .(1)、若 , 且该二次函数的图象过点 , 求的值;(2)、如图所示,在平面直角坐标系中,该二次函数的图象与轴交于点 , 且 , 点D在上且在第二象限内,点在轴正半轴上,连接 , 且线段交轴正半轴于点 , .
①求证: .
②当点在线段上,且 . 的半径长为线段的长度的倍,若 , 求的值.
22. 如图,二次函数的图象与轴的正半轴交于点A,经过点A的直线与该函数图象交于点 , 与轴交于点C.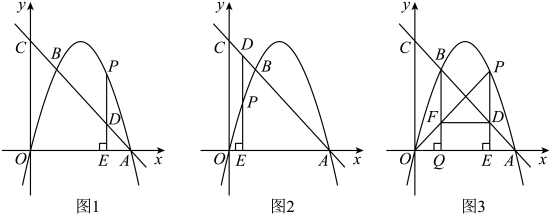 (1)、求直线的函数表达式及点C的坐标;(2)、点是第一象限内二次函数图象上的一个动点,过点作直线轴于点 , 与直线交于点D,设点的横坐标为 .
(1)、求直线的函数表达式及点C的坐标;(2)、点是第一象限内二次函数图象上的一个动点,过点作直线轴于点 , 与直线交于点D,设点的横坐标为 .①当时,求的值;
②当点在直线上方时,连接 , 过点作轴于点 , 与交于点 , 连接 . 设四边形的面积为 , 求关于的函数表达式,并求出S的最大值.
23. 如图1,在平面直角坐标系中,已知二次函数的图象与x轴交于点 , , 与轴交于点 .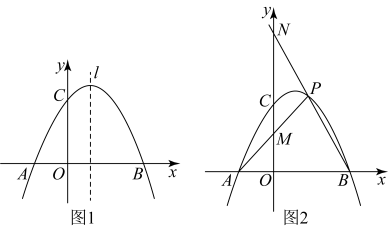 (1)、求抛物线的解析式;(2)、已知为抛物线上一点,为抛物线对称轴上一点,以 , , 为顶点的三角形是等腰直角三角形,且 , 求出点的坐标;(3)、如图 , 为第一象限内抛物线上一点,连接交轴于点 , 连接并延长交轴于点 , 在点运动过程中,是否为定值?若是,求出这个定值;若不是,请说明理由.24. 如图,在平面直角坐标系中,抛物线与x轴交于 , 两点.与y轴交于点 .
(1)、求抛物线的解析式;(2)、已知为抛物线上一点,为抛物线对称轴上一点,以 , , 为顶点的三角形是等腰直角三角形,且 , 求出点的坐标;(3)、如图 , 为第一象限内抛物线上一点,连接交轴于点 , 连接并延长交轴于点 , 在点运动过程中,是否为定值?若是,求出这个定值;若不是,请说明理由.24. 如图,在平面直角坐标系中,抛物线与x轴交于 , 两点.与y轴交于点 .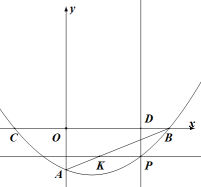 (1)、求该抛物线的函数表达式;(2)、若点P是直线下方抛物线上的一动点,过点P作x轴的平行线交于点K,过点P作y轴的平行线交x轴于点D,求与的最大值及此时点P的坐标;(3)、在抛物线的对称轴上是否存在一点M,使得是以为一条直角边的直角三角形:若存在,请求出点M的坐标,若不存在,请说明理由.25. 已知抛物线交轴于两点,为抛物线的顶点,为抛物线上不与重合的相异两点,记中点为 , 直线的交点为 .(1)、求抛物线的函数表达式;(2)、若 , 且 , 求证:三点共线;(3)、小明研究发现:无论在抛物线上如何运动,只要三点共线,中必存在面积为定值的三角形.请直接写出其中面积为定值的三角形及其面积,不必说明理由.26. 已知抛物线过点和点 , 与轴交于点 .
(1)、求该抛物线的函数表达式;(2)、若点P是直线下方抛物线上的一动点,过点P作x轴的平行线交于点K,过点P作y轴的平行线交x轴于点D,求与的最大值及此时点P的坐标;(3)、在抛物线的对称轴上是否存在一点M,使得是以为一条直角边的直角三角形:若存在,请求出点M的坐标,若不存在,请说明理由.25. 已知抛物线交轴于两点,为抛物线的顶点,为抛物线上不与重合的相异两点,记中点为 , 直线的交点为 .(1)、求抛物线的函数表达式;(2)、若 , 且 , 求证:三点共线;(3)、小明研究发现:无论在抛物线上如何运动,只要三点共线,中必存在面积为定值的三角形.请直接写出其中面积为定值的三角形及其面积,不必说明理由.26. 已知抛物线过点和点 , 与轴交于点 . (1)、求抛物线的解析式;(2)、如图1,连接 , 点在线段上(与点不重合),点是的中点,连接 , 过点作交于点 , 连接 , 当面积是面积的3倍时,求点的坐标;(3)、如图2,点是抛物线上对称轴右侧的点,是轴正半轴上的动点,若线段上存在点(与点不重合),使得 , 求的取值范围.27. 如图1,平面直角坐标系中,抛物线过点 , 和 , 连接 , 点为抛物线上一动点,过点作轴交直线于点 , 交轴于点 .
(1)、求抛物线的解析式;(2)、如图1,连接 , 点在线段上(与点不重合),点是的中点,连接 , 过点作交于点 , 连接 , 当面积是面积的3倍时,求点的坐标;(3)、如图2,点是抛物线上对称轴右侧的点,是轴正半轴上的动点,若线段上存在点(与点不重合),使得 , 求的取值范围.27. 如图1,平面直角坐标系中,抛物线过点 , 和 , 连接 , 点为抛物线上一动点,过点作轴交直线于点 , 交轴于点 . (1)、直接写出抛物线和直线的解析式;(2)、如图2,连接 , 当为等腰三角形时,求的值;(3)、当点在运动过程中,在轴上是否存在点 , 使得以 , , 为顶点的三角形与以 , , 为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.
(1)、直接写出抛物线和直线的解析式;(2)、如图2,连接 , 当为等腰三角形时,求的值;(3)、当点在运动过程中,在轴上是否存在点 , 使得以 , , 为顶点的三角形与以 , , 为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.
-