2023年中考数学真题分类汇编(全国版):二次函数(1)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 如图.抛物线与x轴交于点和点 , 与y轴交于点C.下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y随x的增大而增大;⑤(m为任意实数)其中正确的个数是( )
 A、1个 B、2个 C、3个 D、4个2. 已知二次函数 , 下列说法正确的是( )A、对称轴为 B、顶点坐标为 C、函数的最大值是-3 D、函数的最小值是-33. 在平面直角坐标系中,抛物线 , 满足 , 已知点 , , 在该抛物线上,则m,n,t的大小关系为( )A、 B、 C、 D、4. 已知,二次数的图象如图所示,则点所在的象限是( )
A、1个 B、2个 C、3个 D、4个2. 已知二次函数 , 下列说法正确的是( )A、对称轴为 B、顶点坐标为 C、函数的最大值是-3 D、函数的最小值是-33. 在平面直角坐标系中,抛物线 , 满足 , 已知点 , , 在该抛物线上,则m,n,t的大小关系为( )A、 B、 C、 D、4. 已知,二次数的图象如图所示,则点所在的象限是( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,抛物线与x轴交于点A,B,与y轴交于点C,对称轴为直线 , 若点A的坐标为 , 则下列结论正确的是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,抛物线与x轴交于点A,B,与y轴交于点C,对称轴为直线 , 若点A的坐标为 , 则下列结论正确的是( ) A、 B、 C、是关于x的一元二次方程的一个根 D、点 , 在抛物线上,当时6. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0;③3a+c>0;④若A( , ),B( , )(其中<)是抛物线上的两点,且+>2,则> , 其中正确的选项是( )
A、 B、 C、是关于x的一元二次方程的一个根 D、点 , 在抛物线上,当时6. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0;③3a+c>0;④若A( , ),B( , )(其中<)是抛物线上的两点,且+>2,则> , 其中正确的选项是( )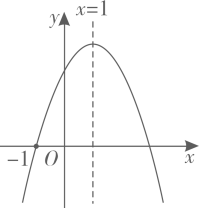 A、①②③ B、①③④ C、②③④ D、①②④7. 在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )A、 B、 C、 D、8. 如图,在四边形中, , , , 若线段在边上运动,且 , 则的最小值是( )
A、①②③ B、①③④ C、②③④ D、①②④7. 在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )A、 B、 C、 D、8. 如图,在四边形中, , , , 若线段在边上运动,且 , 则的最小值是( ) A、 B、 C、 D、10
A、 B、 C、 D、10二、解答题
-
9. 城建部门计划修建一条喷泉步行通道.图1是项目俯视示意图.步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池.图2是主视示意图.喷水装置的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内,当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米.为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩,防水罩的一端固定在喷水装置上的点处,另一端与路面的垂直高度为1.8米,且与喷泉水流的水平距离为0.3米.点到水池外壁的水平距离米,求步行通道的宽 . (结果精确到0.1米)参考数据:

三、综合题
-
10. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .
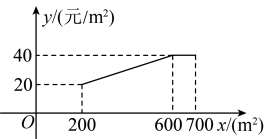 (1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?11. 某大型超市购进一款热销的消毒洗衣液,由于原材料价格上涨,今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元,今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同.当每瓶洗衣液的现售价为36元时,每周可卖出600瓶,为了能薄利多销.该超市决定降价销售,经市场调查发现,这种洗衣液的售价每降价1元,每周的销量可增加100瓶,规定这种消毒洗衣液每瓶的售价不低于进价.(1)、求今年这款消毒洗衣液每瓶进价是多少元;(2)、当这款消毒洗衣液每瓶的售价定为多少元时,这款洗衣液每周的销售利润最大?最大利润是多少元?12. 某景区旅游商店以元的价格采购一款旅游食品加工后出售,销售价格不低于元 , 不高于元 , 经市场调查发现每天的销售量与销售价格(元)之间的函数关系如图所示.
(1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?11. 某大型超市购进一款热销的消毒洗衣液,由于原材料价格上涨,今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元,今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同.当每瓶洗衣液的现售价为36元时,每周可卖出600瓶,为了能薄利多销.该超市决定降价销售,经市场调查发现,这种洗衣液的售价每降价1元,每周的销量可增加100瓶,规定这种消毒洗衣液每瓶的售价不低于进价.(1)、求今年这款消毒洗衣液每瓶进价是多少元;(2)、当这款消毒洗衣液每瓶的售价定为多少元时,这款洗衣液每周的销售利润最大?最大利润是多少元?12. 某景区旅游商店以元的价格采购一款旅游食品加工后出售,销售价格不低于元 , 不高于元 , 经市场调查发现每天的销售量与销售价格(元)之间的函数关系如图所示. (1)、求关于的函数表达式:(2)、当销售价格定为多少时,该商店销售这款食品每天获得的销售利润最大?最大销售利润是多少?【销售利润=(销售价格一采购价格)×销售量】13. 一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为 .
(1)、求关于的函数表达式:(2)、当销售价格定为多少时,该商店销售这款食品每天获得的销售利润最大?最大销售利润是多少?【销售利润=(销售价格一采购价格)×销售量】13. 一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为 . (1)、求y关于x的函数表达式;(2)、求运动员从起跳点到入水点的水平距离的长.14. 如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形 . 设的长为 , 四边形的面积为 .
(1)、求y关于x的函数表达式;(2)、求运动员从起跳点到入水点的水平距离的长.14. 如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形 . 设的长为 , 四边形的面积为 .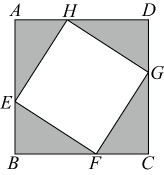 (1)、求关于的函数表达式;(2)、当取何值时,四边形的面积为10?(3)、四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.15. 某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:
(1)、求关于的函数表达式;(2)、当取何值时,四边形的面积为10?(3)、四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.15. 某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:时间:第x(天)
日销售价(元/件)
50
日销售量(件)
( , x为整数)
设该商品的日销售利润为w元.
(1)、直接写出w与x的函数关系式;(2)、该商品在第几天的日销售利润最大?最大日销售利润是多少?16. 定义:在平面直角坐标系中,当点N在图形M的内部,或在图形M上,且点N的横坐标和纵坐标相等时,则称点N为图形M的“梦之点”. (1)、如图①,矩形的顶点坐标分别是 , , , , 在点 , , 中,是矩形“梦之点”的是;(2)、点是反比例函数图象上的一个“梦之点”,则该函数图象上的另一个“梦之点”H的坐标是 , 直线的解析式是 . 当时,x的取值范围是 .(3)、如图②,已知点A,B是抛物线上的“梦之点”,点C是抛物线的顶点,连接 , , , 判断的形状,并说明理由.17. 已知抛物线与x轴交于两点,与y轴交于点 , 点P为第一象限抛物线上的点,连接 .
(1)、如图①,矩形的顶点坐标分别是 , , , , 在点 , , 中,是矩形“梦之点”的是;(2)、点是反比例函数图象上的一个“梦之点”,则该函数图象上的另一个“梦之点”H的坐标是 , 直线的解析式是 . 当时,x的取值范围是 .(3)、如图②,已知点A,B是抛物线上的“梦之点”,点C是抛物线的顶点,连接 , , , 判断的形状,并说明理由.17. 已知抛物线与x轴交于两点,与y轴交于点 , 点P为第一象限抛物线上的点,连接 .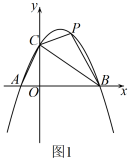
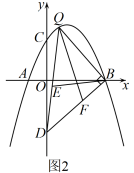
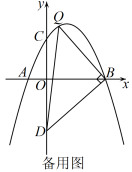 (1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.
(1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.①求m的值;
②设的面积为S,若 , 请直接写出k的取值范围.
18. 如图,在平面直角坐标系中,抛物线上有两点 , 其中点的横坐标为 , 点的横坐标为 , 抛物线过点 . 过作轴交抛物线另一点为点 . 以长为边向上构造矩形 . (1)、求抛物线的解析式;(2)、将矩形向左平移个单位,向下平移个单位得到矩形 , 点的对应点落在抛物线上.
(1)、求抛物线的解析式;(2)、将矩形向左平移个单位,向下平移个单位得到矩形 , 点的对应点落在抛物线上.①求关于的函数关系式,并直接写出自变量的取值范围;
②直线交抛物线于点 , 交抛物线于点 . 当点为线段的中点时,求的值;
③抛物线与边分别相交于点 , 点在抛物线的对称轴同侧,当时,求点的坐标.
19. 如图,抛物线与轴交于点和点 , 与轴交于点 , 抛物线的对称轴交轴于点 , 过点作直线轴,过点作 , 交直线于点 . (1)、求抛物线的解析式;(2)、如图,点为第三象限内抛物线上的点,连接和交于点 , 当时.求点的坐标;(3)、在(2)的条件下,连接 , 在直线上是否存在点 , 使得?若存在,请直接写出点F的坐标;若不存在,请说明理由.20. 我们约定:若关于x的二次函数与同时满足 , 则称函数与函数互为“美美与共”函数.根据该约定,解答下列问题:(1)、若关于x的二次函数与互为“美美与共”函数,求k,m,n的值;(2)、对于任意非零实数r,s,点与点始终在关于x的函数的图像上运动,函数与互为“美美与共”函数.
(1)、求抛物线的解析式;(2)、如图,点为第三象限内抛物线上的点,连接和交于点 , 当时.求点的坐标;(3)、在(2)的条件下,连接 , 在直线上是否存在点 , 使得?若存在,请直接写出点F的坐标;若不存在,请说明理由.20. 我们约定:若关于x的二次函数与同时满足 , 则称函数与函数互为“美美与共”函数.根据该约定,解答下列问题:(1)、若关于x的二次函数与互为“美美与共”函数,求k,m,n的值;(2)、对于任意非零实数r,s,点与点始终在关于x的函数的图像上运动,函数与互为“美美与共”函数.①求函数的图像的对称轴;
②函数的图像是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由;
(3)、在同一平面直角坐标系中,若关于x的二次函数与它的“美美与共”函数的图像顶点分别为点A,点B,函数的图像与x轴交于不同两点C,D,函数的图像与x轴交于不同两点E,F.当时,以A,B,C,D为顶点的四边形能否为正方形?若能,求出该正方形面积的取值范围;若不请说明理由.21. 已知二次函数的图像与轴交于点 , 且经过点和点 .(1)、请直接写出 , 的值;(2)、直线交轴于点 , 点是二次函数图像上位于直线下方的动点,过点作直线的垂线,垂足为 .①求的最大值;
②若中有一个内角是的两倍,求点的横坐标.
22. 如图,在平面直角坐标系中,已知二次函数的图象与x轴交于点和点两点,与y轴交于点 . 点D为线段上的一动点. (1)、求二次函数的表达式;(2)、如图1,求周长的最小值;(3)、如图2,过动点D作交抛物线第一象限部分于点P,连接 , 记与的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.23. 如图,在平面直角坐标系中,抛物线交轴于点 , 顶点坐标为 . 抛物线交轴于点 , 顶点坐标为 .
(1)、求二次函数的表达式;(2)、如图1,求周长的最小值;(3)、如图2,过动点D作交抛物线第一象限部分于点P,连接 , 记与的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.23. 如图,在平面直角坐标系中,抛物线交轴于点 , 顶点坐标为 . 抛物线交轴于点 , 顶点坐标为 . (1)、连接 , 求线段的长;(2)、点在抛物线上,点在抛物线上.比较大小:;(3)、若点在抛物线上, , 求的取值范围.24. 如图,在平而直角坐标系中,二次函数的图象与轴分别交于点 , 顶点为 . 连接 , 将线段绕点按顺时针方向旋转得到线段 , 连接 . 点分别在线段上,连接与交于点 .
(1)、连接 , 求线段的长;(2)、点在抛物线上,点在抛物线上.比较大小:;(3)、若点在抛物线上, , 求的取值范围.24. 如图,在平而直角坐标系中,二次函数的图象与轴分别交于点 , 顶点为 . 连接 , 将线段绕点按顺时针方向旋转得到线段 , 连接 . 点分别在线段上,连接与交于点 .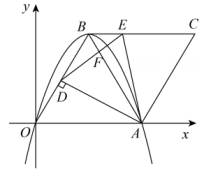 (1)、求点的坐标;(2)、随着点线段上运动.
(1)、求点的坐标;(2)、随着点线段上运动.①的大小是否发生变化?请说明理由;
②线段的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由;
(3)、当线段的中点在该二次函数的因象的对称轴上时,的面积为.25. 如图1,在平面直角坐标系中,已知抛物线与轴交于点 , 与轴交于点 , 顶点为 , 连接 . (1)、抛物线的解析式为;(直接写出结果)(2)、在图1中,连接并延长交的延长线于点 , 求的度数;(3)、如图2,若动直线与抛物线交于两点(直线与不重合),连接 , 直线与交于点 . 当时,点的横坐标是否为定值,请说明理由.
(1)、抛物线的解析式为;(直接写出结果)(2)、在图1中,连接并延长交的延长线于点 , 求的度数;(3)、如图2,若动直线与抛物线交于两点(直线与不重合),连接 , 直线与交于点 . 当时,点的横坐标是否为定值,请说明理由.
-