2023年中考数学真题分类汇编(全国版):反比例函数(2)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
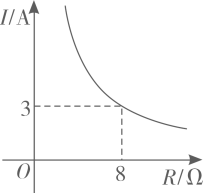
1. 已知蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
 A、 B、 C、 D、2. 关于反比例函数 , 下列结论正确的是( )A、图像位于第二、四象限 B、图像与坐标轴有公共点 C、图像所在的每一个象限内,随的增大而减小 D、图像经过点 , 则3. 某反比例函数图象上四个点的坐标分别为 , 则,的大小关系为( )A、 B、 C、 D、4. 已知压力、压强与受力面积之间有如下关系式: . 当F为定值时,下图中大致表示压强p与受力面积S之间函数关系的是( )A、
A、 B、 C、 D、2. 关于反比例函数 , 下列结论正确的是( )A、图像位于第二、四象限 B、图像与坐标轴有公共点 C、图像所在的每一个象限内,随的增大而减小 D、图像经过点 , 则3. 某反比例函数图象上四个点的坐标分别为 , 则,的大小关系为( )A、 B、 C、 D、4. 已知压力、压强与受力面积之间有如下关系式: . 当F为定值时,下图中大致表示压强p与受力面积S之间函数关系的是( )A、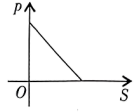 B、
B、 C、
C、 D、
D、 5. 如图,反比例函数的图象与过点的直线相交于、两点.已知点的坐标为 , 点为轴上任意一点.如果 , 那么点的坐标为( )
5. 如图,反比例函数的图象与过点的直线相交于、两点.已知点的坐标为 , 点为轴上任意一点.如果 , 那么点的坐标为( ) A、 B、 C、或 D、或6. 若点都在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、7. 函数的大致图像是( )A、
A、 B、 C、或 D、或6. 若点都在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、7. 函数的大致图像是( )A、 B、
B、 C、
C、 D、
D、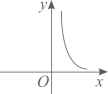 8. 如图,在平面直角坐标系中,点A、B分别在y,x轴上,轴.点M、N分别在线段、上, , , 反比例函数的图象经过M、N两点,P为x正半轴上一点,且 , 的面积为3,则k的值为( )
8. 如图,在平面直角坐标系中,点A、B分别在y,x轴上,轴.点M、N分别在线段、上, , , 反比例函数的图象经过M、N两点,P为x正半轴上一点,且 , 的面积为3,则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在平面直角坐标系中,为直角三角形, , , . 若反比例函数的图象经过的中点 , 交于点 , 则 .
 10. 如图,在反比例函数的图象上有等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为 , 则 .
10. 如图,在反比例函数的图象上有等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为 , 则 . 11. 如图,在直角坐标系中,与轴相切于点为的直径,点在函数的图象上,为轴上一点,的面积为6,则的值为 .
11. 如图,在直角坐标系中,与轴相切于点为的直径,点在函数的图象上,为轴上一点,的面积为6,则的值为 . 12. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时, . 当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .13. 在平面直角坐标系中,点在轴的正半轴上,点在直线上,若点的坐标为 , 且均为等边三角形.则点的纵坐标为 .
12. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时, . 当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .13. 在平面直角坐标系中,点在轴的正半轴上,点在直线上,若点的坐标为 , 且均为等边三角形.则点的纵坐标为 .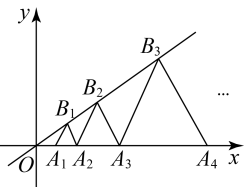 14. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对气缸壁所产生的压强与气缸内气体的体积成反比例,关于的函数图象如图所示.若压强由加压到 , 则气体体积压缩了.
14. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对气缸壁所产生的压强与气缸内气体的体积成反比例,关于的函数图象如图所示.若压强由加压到 , 则气体体积压缩了.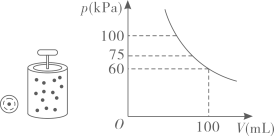 15. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是.
15. 如图,在平面直角坐标系中,函数(为大于0的常数,)图象上的两点 , 满足的边轴,边轴,若的面积为6,则的面积是.
三、综合题
-
16. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 .
 (1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.17. 如图,一次函数的图象与反比例函数的图象交于两点.
(1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.17. 如图,一次函数的图象与反比例函数的图象交于两点. (1)、求一次函数的表达式,并在所给的平面直角坐标系中画出这个一次函数的图象;(2)、观察图象,直接写出不等式的解集;(3)、设直线与x轴交于点C,若为y轴上的一动点,连接 , 当的面积为时,求点P的坐标.18. 如图,正比例函数的图象与反比例函数的图象相交于点A.
(1)、求一次函数的表达式,并在所给的平面直角坐标系中画出这个一次函数的图象;(2)、观察图象,直接写出不等式的解集;(3)、设直线与x轴交于点C,若为y轴上的一动点,连接 , 当的面积为时,求点P的坐标.18. 如图,正比例函数的图象与反比例函数的图象相交于点A. (1)、求点A的坐标.(2)、分别以点O、A为圆心,大于一半的长为半径作圆弧,两弧相交于点B和点C,作直线 , 交x轴于点D.求线段的长.19. 如图,一次函数的图象与反比例函数的图象交于点 . 将点沿轴正方向平移个单位长度得到点为轴正半轴上的点,点的横坐标大于点的横坐标,连接的中点在反比例函数的图象上.
(1)、求点A的坐标.(2)、分别以点O、A为圆心,大于一半的长为半径作圆弧,两弧相交于点B和点C,作直线 , 交x轴于点D.求线段的长.19. 如图,一次函数的图象与反比例函数的图象交于点 . 将点沿轴正方向平移个单位长度得到点为轴正半轴上的点,点的横坐标大于点的横坐标,连接的中点在反比例函数的图象上.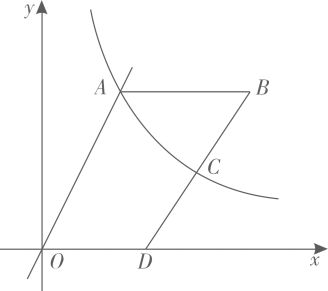 (1)、求的值;(2)、当为何值时,的值最大?最大值是多少?
(1)、求的值;(2)、当为何值时,的值最大?最大值是多少?