2023年中考数学真题分类汇编(全国版):反比例函数(1)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 从1,2,3这三个数中随机抽取两个不同的数,分别记作和.若点的坐标记作 , 则点在双曲线上的概率是( )A、 B、 C、 D、2. 已知蓄电池两端电压为定值,电流与成反比例函数关系.当时, , 则当时,的值为( )A、 B、 C、 D、3. 在反比例函数的图象上有两点 , 当时,有 , 则的取值范围是( )A、 B、 C、 D、4. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( )
 A、 B、 C、 D、5. 如图,在平面直角坐标系中,三个顶点的坐标分别为 , , , 与关于直线OB对称,反比例函数的图象与交于点.若 , 则的值为( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,三个顶点的坐标分别为 , , , 与关于直线OB对称,反比例函数的图象与交于点.若 , 则的值为( ) A、 B、 C、 D、6. 在平面直角坐标系中,点A在y轴的正半轴上,平行于x轴,点B,C的横坐标都是3, , 点D在上,且其横坐标为1,若反比例函数()的图象经过点B,D,则k的值是( )
A、 B、 C、 D、6. 在平面直角坐标系中,点A在y轴的正半轴上,平行于x轴,点B,C的横坐标都是3, , 点D在上,且其横坐标为1,若反比例函数()的图象经过点B,D,则k的值是( )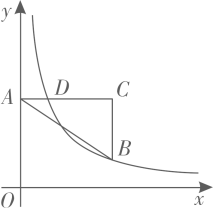 A、1 B、2 C、3 D、7. 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系().下列反映电流I与电阻R之间函数关系的图象大致是( )A、
A、1 B、2 C、3 D、7. 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系().下列反映电流I与电阻R之间函数关系的图象大致是( )A、 B、
B、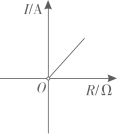 C、
C、 D、
D、 8. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为 , 则点的坐标为( )
8. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为 , 则点的坐标为( ) A、 B、 C、 D、9. 下列哪个点在反比例函数的图像上?( )A、 B、 C、 D、10. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )
A、 B、 C、 D、9. 下列哪个点在反比例函数的图像上?( )A、 B、 C、 D、10. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )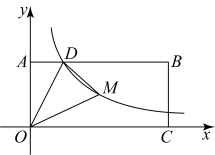 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1·k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是 .
 12. 如图,与位于平面直角坐标系中, , , , 若 , 反比例函数恰好经过点C,则 .
12. 如图,与位于平面直角坐标系中, , , , 若 , 反比例函数恰好经过点C,则 . 13. 某蓄电池的电压为 , 使用此蓄电池时,电流(单位:)与电阻(单位:)的函数表达式为 , 当时,的值为 .14. 如图,点A在反比例函数图象的一支上,点B在反比例函数图象的一支上,点C,D在x轴上,若四边形ABCD是面积为9的正方形,则实数k的值为.
13. 某蓄电池的电压为 , 使用此蓄电池时,电流(单位:)与电阻(单位:)的函数表达式为 , 当时,的值为 .14. 如图,点A在反比例函数图象的一支上,点B在反比例函数图象的一支上,点C,D在x轴上,若四边形ABCD是面积为9的正方形,则实数k的值为. 15. 如图,在矩形和正方形中,点在轴正半轴上,点 , 均在轴正半轴上,点在边上, , 若点 , 在同一个反比例函数的图象上,则这个反比例函数的表达式是 .
15. 如图,在矩形和正方形中,点在轴正半轴上,点 , 均在轴正半轴上,点在边上, , 若点 , 在同一个反比例函数的图象上,则这个反比例函数的表达式是 . 16. 如图,点A(2,2)在双曲线上,将直线OA向上平移若干个单位长度交y轴于点B,交双曲线于点C. 若BC=2,则点C的坐标是 .
16. 如图,点A(2,2)在双曲线上,将直线OA向上平移若干个单位长度交y轴于点B,交双曲线于点C. 若BC=2,则点C的坐标是 .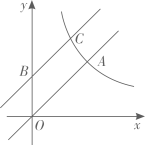 17. 如图,在平面直角坐标系中,O为坐标原点,垂直于x轴,以为对称轴作的轴对称图形,对称轴与线段相交于点F,点D的对应点B恰好落在反比例函数的图象上,点O、E的对应点分别是点C、A.若点A为的中点,且 , 则k的值为 .
17. 如图,在平面直角坐标系中,O为坐标原点,垂直于x轴,以为对称轴作的轴对称图形,对称轴与线段相交于点F,点D的对应点B恰好落在反比例函数的图象上,点O、E的对应点分别是点C、A.若点A为的中点,且 , 则k的值为 .
三、综合题
-
18. 如图,一次函数与函数为的图象交于两点.
 (1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.19. 如图,点A在反比例函数的图象上,轴于点B, , .
(1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.19. 如图,点A在反比例函数的图象上,轴于点B, , . (1)、求反比例函数的解析式;(2)、点C在这个反比例函数图象上,连接并延长交x轴于点D,且 , 求点C的坐标.20. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作 , 连接BF.
(1)、求反比例函数的解析式;(2)、点C在这个反比例函数图象上,连接并延长交x轴于点D,且 , 求点C的坐标.20. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作 , 连接BF. (1)、求k的值;(2)、求扇形AOC的半径及圆心角的度数;(3)、请直接写出图中阴影部分面积之和.21. 如图,在平面直角坐标系中,四边形是矩形,反比例函数的图象分别与交于点和点 , 且点为的中点.
(1)、求k的值;(2)、求扇形AOC的半径及圆心角的度数;(3)、请直接写出图中阴影部分面积之和.21. 如图,在平面直角坐标系中,四边形是矩形,反比例函数的图象分别与交于点和点 , 且点为的中点. (1)、求反比例函数的表达式和点的坐标;(2)、若一次函数与反比例函数的图象相交于点 , 当点在反比例函数图象上之间的部分时(点可与点重合),直接写出的取值范围.
(1)、求反比例函数的表达式和点的坐标;(2)、若一次函数与反比例函数的图象相交于点 , 当点在反比例函数图象上之间的部分时(点可与点重合),直接写出的取值范围.