2023年中考数学真题分类汇编(全国版):一次方程(4)
试卷更新日期:2023-07-23 类型:二轮复习
一、填空题
-
1. 如图,直线(k为常数,)与x,y轴分别交于点A,B,则的值是 .

二、综合题
-
2. 如图,一次函数图象与反比例函数图象交于点 , , 与x轴交于点C,与y轴交于点D.
 (1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.3. 某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且 , 售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式(1)、若产销A,B两种产品的日利润分别为元,元,请分别写出 , 与x的函数关系式,并写出x的取值范围;(2)、分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)(3)、为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】4. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .
(1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.3. 某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且 , 售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式(1)、若产销A,B两种产品的日利润分别为元,元,请分别写出 , 与x的函数关系式,并写出x的取值范围;(2)、分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)(3)、为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】4. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .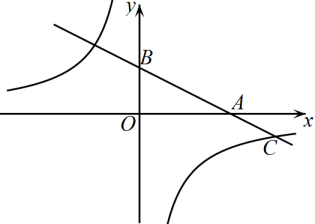 (1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.5. 如图,在直角坐标系中,点在直线上,过点的直线交轴于点.
(1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.5. 如图,在直角坐标系中,点在直线上,过点的直线交轴于点. (1)、求m的值和直线AB的函数表达式。(2)、若点在线段AB上,点在直线上,求的最大值.6. 一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地 , 匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象.
(1)、求m的值和直线AB的函数表达式。(2)、若点在线段AB上,点在直线上,求的最大值.6. 一条笔直的路上依次有三地,其中两地相距1000米.甲、乙两机器人分别从两地同时出发,去目的地 , 匀速而行.图中分别表示甲、乙机器人离地的距离(米)与行走时间(分钟)的函数关系图象. (1)、求所在直线的表达式.(2)、出发后甲机器人行走多少时间,与乙机器人相遇?(3)、甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.7. 如图,一次函数的图像与反比例函数的图像交于 , 两点.( , , 为常数)
(1)、求所在直线的表达式.(2)、出发后甲机器人行走多少时间,与乙机器人相遇?(3)、甲机器人到地后,再经过1分钟乙机器人也到地,求两地间的距离.7. 如图,一次函数的图像与反比例函数的图像交于 , 两点.( , , 为常数) (1)、求一次函数和反比例函数的解析式;(2)、根据图像直接写出不等式的解集;(3)、为轴上一点,若的面积为 , 求点的坐标.8. 如图,一次函数的图象与反比例函数的图象交于点 , 与x轴交于点B, 与y轴交于点 .
(1)、求一次函数和反比例函数的解析式;(2)、根据图像直接写出不等式的解集;(3)、为轴上一点,若的面积为 , 求点的坐标.8. 如图,一次函数的图象与反比例函数的图象交于点 , 与x轴交于点B, 与y轴交于点 . (1)、求m的值和一次函数的表达式;(2)、已知P为反比例函数图象上的一点, , 求点P的坐标.9. 某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学,上午8:00,军车在离营地
(1)、求m的值和一次函数的表达式;(2)、已知P为反比例函数图象上的一点, , 求点P的坐标.9. 某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学,上午8:00,军车在离营地 地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.  (1)、求大巴离营地的路程s与所用时间t的函数表达式及a的值,(2)、求部队官兵在仓库领取物资所用的时间.10. 2023年7月28日至8月8日,第31届世界大学生运动会将在成都举行. “当好东道主,热情迎嘉宾”,成都某知名小吃店计划购买A,B两种食材制作小吃. 已知购买1千克A种食材和1千克B种食材共需68元,购买5千克A种食材和3千克B种食材共需280元.(1)、求A,B两种食材的单价;(2)、该小吃店计划购买两种食材共36千克,其中购买A种食材千克数不少于B种食材千克数的2倍,当A,B两种食材分别购买多少千克时,总费用最少?并求出最少总费用.11. 如图,点在反比例函数图象上.一次函数的图象经过点A,分别交x轴,y轴于点B,C,且与的面积比为 .
(1)、求大巴离营地的路程s与所用时间t的函数表达式及a的值,(2)、求部队官兵在仓库领取物资所用的时间.10. 2023年7月28日至8月8日,第31届世界大学生运动会将在成都举行. “当好东道主,热情迎嘉宾”,成都某知名小吃店计划购买A,B两种食材制作小吃. 已知购买1千克A种食材和1千克B种食材共需68元,购买5千克A种食材和3千克B种食材共需280元.(1)、求A,B两种食材的单价;(2)、该小吃店计划购买两种食材共36千克,其中购买A种食材千克数不少于B种食材千克数的2倍,当A,B两种食材分别购买多少千克时,总费用最少?并求出最少总费用.11. 如图,点在反比例函数图象上.一次函数的图象经过点A,分别交x轴,y轴于点B,C,且与的面积比为 . (1)、求反比例函数和一次函数的解析式;(2)、请直接写出时,x的取值范围.12. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.
(1)、求反比例函数和一次函数的解析式;(2)、请直接写出时,x的取值范围.12. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.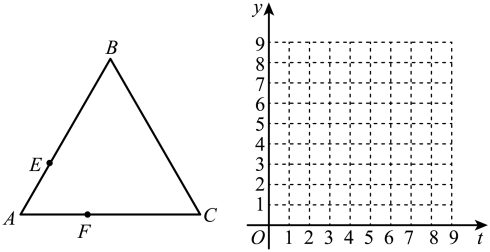 (1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.13. 我市“共富工坊"问梅借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同,看图解答下列问题:
(1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.13. 我市“共富工坊"问梅借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同,看图解答下列问题: (1)、直接写出员工生产多少件产品时,两种方案付给的报酬一样多;(2)、求方案二y关于x的函数表达式;(3)、如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.14. 在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点 , 点P是抛物线上的一个动点.
(1)、直接写出员工生产多少件产品时,两种方案付给的报酬一样多;(2)、求方案二y关于x的函数表达式;(3)、如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.14. 在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点 , 点P是抛物线上的一个动点. (1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.15. 在平面直角坐标系中,为坐标原点,抛物线经过点 , , 对称轴过点 , , 直线过点 , 且垂直于轴.过点的直线交抛物线于点、 , 交直线于点 , 其中点、Q在抛物线对称轴的左侧.
(1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.15. 在平面直角坐标系中,为坐标原点,抛物线经过点 , , 对称轴过点 , , 直线过点 , 且垂直于轴.过点的直线交抛物线于点、 , 交直线于点 , 其中点、Q在抛物线对称轴的左侧.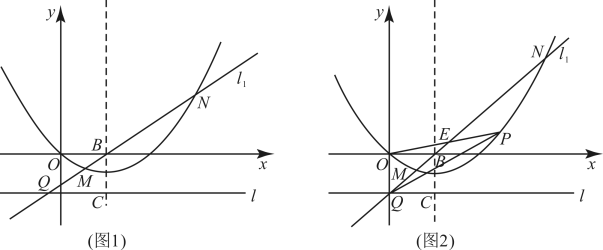 (1)求抛物线的解析式;(1)、如图1,当时,求点的坐标;(2)、如图2,当点恰好在轴上时,为直线下方的抛物线上一动点,连接、 , 其中交于点 , 设的面积为 , 的面积为 . 求的最大值.16. 如图,抛物线过点 .
(1)求抛物线的解析式;(1)、如图1,当时,求点的坐标;(2)、如图2,当点恰好在轴上时,为直线下方的抛物线上一动点,连接、 , 其中交于点 , 设的面积为 , 的面积为 . 求的最大值.16. 如图,抛物线过点 .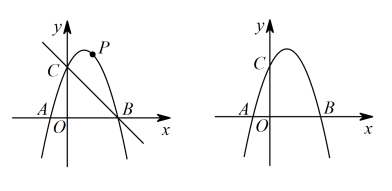 (1)、求抛物线的解析式;(2)、设点是直线上方抛物线上一点,求出的最大面积及此时点的坐标;(3)、若点是抛物线对称轴上一动点,点为坐标平面内一点,是否存在以为边,点为顶点的四边形是菱形,若存在,请直接写出点的坐标;若不存在,请说明理由.17. 阅读理解题:
(1)、求抛物线的解析式;(2)、设点是直线上方抛物线上一点,求出的最大面积及此时点的坐标;(3)、若点是抛物线对称轴上一动点,点为坐标平面内一点,是否存在以为边,点为顶点的四边形是菱形,若存在,请直接写出点的坐标;若不存在,请说明理由.17. 阅读理解题:阅读材料:
如图1,四边形是矩形,是等腰直角三角形,记为、为 , 若 , 则 .

证明:设 , ∵ , ∴ ,
易证
∴ ,
∴
∴ ,
若时,当 , 则 .
同理:若时,当 , 则 .
根据上述材料,完成下列问题:
如图2,直线与反比例函数的图象交于点 , 与轴交于点 . 将直线绕点顺时针旋转后的直线与轴交于点 , 过点作轴于点 , 过点作轴于点 , 已知 .
 (1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.18. 如图,已知抛物线与轴交于和两点,与轴交于点 . 直线过抛物线的顶点 .
(1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.18. 如图,已知抛物线与轴交于和两点,与轴交于点 . 直线过抛物线的顶点 . (1)、求抛物线的函数解析式;(2)、若直线与抛物线交于点 , 与直线交于点 .
(1)、求抛物线的函数解析式;(2)、若直线与抛物线交于点 , 与直线交于点 .①当取得最大值时,求的值和的最大值;
②当是等腰三角形时,求点的坐标.
19. 如图,在平面直角坐标系中,抛物线与轴交于点 , , 与轴交于点 , 其中 , .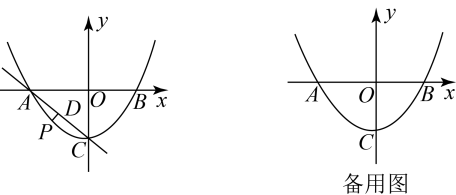 (1)、求该抛物线的表达式;(2)、点是直线下方抛物线上一动点,过点作于点 , 求的最大值及此时点的坐标;(3)、在(2)的条件下,将该抛物线向右平移个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上任意一点.写出所有使得以为腰的是等腰三角形的点的坐标,并把求其中一个点的坐标的过程写出来.
(1)、求该抛物线的表达式;(2)、点是直线下方抛物线上一动点,过点作于点 , 求的最大值及此时点的坐标;(3)、在(2)的条件下,将该抛物线向右平移个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上任意一点.写出所有使得以为腰的是等腰三角形的点的坐标,并把求其中一个点的坐标的过程写出来.
-