2023年中考数学真题分类汇编（全国版）：一次方程（3）

试卷更新日期：2023-07-23 类型：二轮复习

进入出卷网下载

一、填空题

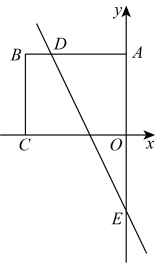
1. 若直线 $y = x$ 向上平移3个单位长度后经过点 $(2 ， m)$ ，则 $m$ 的值为．

查看试题解析
2. 如图，在平面直角坐标系 $x O y$ 中，点B的坐标为 $(- 8 ， 6)$ ，过点B分别作x轴、y轴的垂线，垂足分别为点C、点A，直线 $y = - 2 x - 6$ 与 $A B$ 交于点D．与y轴交于点E．动点M在线段 $B C$ 上，动点N在直线 $y = - 2 x - 6$ 上，若 $△ A M N$ 是以点N为直角顶点的等腰直角三角形，则点M的坐标为

查看试题解析
3. 如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $A (- 3 ， 0)$ ，顶点为 $M (- 1 ， m)$ ，且抛物线与 $y$ 轴的交点B在 $(0 ， - 2)$ 和 $(0 ， - 3)$ 之间（不含端点），则下列结论：

①当 $- 3 \leq x \leq 1$ 时， $y \leq 1$ ；

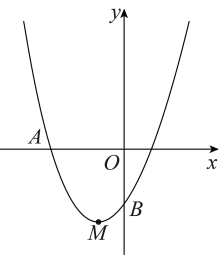
②当 $△ A B M$ 的面积为 $\frac{3 \sqrt{3}}{2}$ 时， $a = \frac{\sqrt{3}}{2}$ ；

③当 $△ A B M$ 为直角三角形时，在 $△ A O B$ 内存在唯一点P，使得 $P A + P O + P B$ 的值最小，最小值的平方为 $18 + 9 \sqrt{3}$ ．

其中正确的结论是．（填写所有正确结论的序号）

查看试题解析
4. 如图，直线 $y = - \frac{1}{3} x + 2$ 与x轴，y轴分别交于A，B两点，点D是线段AB上一动点，点H是直线 $y = - \frac{4}{3} x + 2$ 上的一动点，动点 $E (m ， 0) ， F (m + 3 ， 0)$ ，连接 $B E ， D F ， H D$ ．当 $B E + D F$ 取最小值时， $3 B H + 5 D H$ 的最小值是．

查看试题解析

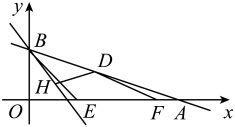
二、综合题

5. 如图，直线 $y = k x + b (k ， b$ 为常数 $)$ 与双曲线 $y = \frac{m}{x}$ （ $m$ 为常数）相交于 $A (2 ， a)$ ， $B (- 1 ， 2)$ 两点．

(1)、求直线 $y = k x + b$ 的解析式；

(2)、在双曲线 $y = \frac{m}{x}$ 上任取两点 $M (x_{1} ， y_{1})$ 和 $N (x_{2} ， y_{2})$ ，若 $x_{1} < x_{2}$ ，试确定 $y_{1}$ 和 $y_{2}$ 的大小关系，并写出判断过程；

(3)、请直接写出关于 $x$ 的不等式 $k x + b > \frac{m}{x}$ 的解集．

查看试题解析
6. 某花店每天购进 $16$ 支某种花，然后出售．如果当天售不完，那么剩下的这种花进行作废处理、该花店记录了 $10$ 天该种花的日需求量n（n为正整数，单位：支），统计如下表：
日需求量n
          $13$
          $14$
          $15$
          $16$
          $17$
          $18$
天数
1
1
2
4
1
1

(1)、求该花店在这 $10$ 天中出现该种花作废处理情形的天数；

(2)、当 $n < 16$ 时，日利润y（单位：元）关于n的函数表达式为： $y = 10 n - 80$ ；当 $n \geq 16$ 时，日利润为 $80$ 元．
①当 $n = 14$ 时，间该花店这天的利润为多少元？
②求该花店这 $10$ 天中日利润为 $70$ 元的日需求量的频率．

查看试题解析
7. 如图，已知一次函数 $y = k x + 6$ 的图象与反比例函数 $y = \frac{m}{x} (m > 0)$ 的图象交于 $A (3 ， 4)$ ， B两点，与x轴交于点C，将直线 $A B$ 沿y轴向上平移3个单位长度后与反比例函数图象交于点D，E．

(1)、求k，m的值及C点坐标；

(2)、连接 $A D$ ， $C D$ ，求 $△ A C D$ 的面积．

查看试题解析
8. 如图，在平面直角坐标系中，一次函数 $y = m x + n$ 与反比例函数 $y = \frac{k}{x}$ 的图象在第一象限内交于 $A (a ， 4)$ 和 $B (4 ， 2)$ 两点，直线 $A B$ 与x轴相交于点C，连接 $O A$ ．

(1)、求一次函数与反比例函数的表达式；

(2)、当 $x > 0$ 时，请结合函数图象，直接写出关于x的不等式 $m x + n ≥ \frac{k}{x}$ 的解集；

(3)、过点B作 $B D$ 平行于x轴，交 $O A$ 于点D，求梯形 $O C B D$ 的面积．

查看试题解析
9. 为了振兴乡村经济，增加村民收入，某村委会干部带领村民在网上直播推销农产品，在试销售的30天中，第x天（ $1 \leq x \leq 30$ 且x为整数）的售价p（元/千克）与x的函数关系式 $p = {\begin{array}{l} m x + n (1 \leq x < 20) \\ 30 (20 \leq x \leq 30) \end{array}$ （且x为整数），销量q（千克）与x的函数关系式为 $q = x + 10$ ，已知第5天售价为50元/千克，第10天售价为40元/千克，设第x天的销售额为W元

(1)、 $m =$ ， $n =$ ；

(2)、求第x天的销售额W元与x之间的函数关系式；

(3)、在试销售的30天中，销售额超过1000元的共有多少天？

查看试题解析
10. 某食用油的沸点温度远高于水的沸点温度．小聪想用刻度不超过 $100 ° C$ 的温度计测算出这种食用油沸点的温度．在老师的指导下，他在锅中倒入一些这种食用油均匀加热，并每隔 $10 s$ 测量一次锅中油温，得到的数据记录如下：

时间t/s

0

10

20

30

40

油温y/ $° C$

10

30

50

70

90

(1)、小聪在直角坐标系中描出了表中数据对应的点．经老师介绍，在这种食用油达到沸点前，锅中油温y（单位： $° C$ ）与加热的时间t（单位：s）符合初中学习过的某种函数关系，填空：可能是函数关系（请选填“正比例”“一次”“二次”“反比例”）；

(2)、根据以上判断，求y关于t的函数解析式；

(3)、当加热 $110 s$ 时，油沸腾了，请推算沸点的温度．

查看试题解析
11. 随着端午节的临近， $A$ ， $B$ 两家超市开展促销活动，各自推出不同的购物优惠方案，如下表：

$A$ 超市
$B$ 超市
优惠方案
所有商品按八折出售
购物金额每满 $100$ 元返 $30$ 元

(1)、当购物金额为 $80$ 元时，选择超市（填“ $A$ ”或“ $B$ ”）更省钱；
当购物金额为 $130$ 元时，选择超市（填“ $A$ ”或“ $B$ ”）更省钱；

(2)、若购物金额为 $x$ （ $0 \leq x < 200$ ）元时，请分别写出它们的实付金额 $y$ （元）与购物金额 $x$ （元）之间的函数解析式，并说明促销期间如何选择这两家超市去购物更省钱？

(3)、对于 $A$ 超市的优惠方案，随着购物金额的增大，顾客享受的优惠率不变，均为 $20$ %（注： $优惠率 = \frac{购物金额 - 实付金额}{购物金额} \times 100 %$ ）．若在 $B$ 超市购物，购物金额越大，享受的优惠率一定越大吗？请举例说明．

查看试题解析
12. 如图，一次函数 $y = m x + n$ 的图象与 $y$ 轴交于点 $A$ ，与反比例函数 $y = \frac{6}{x} (x > 0)$ 的图象交于点 $B (3 ， a)$ ．

(1)、求点 $B$ 的坐标；

(2)、用 $m$ 的代数式表示 $n$ ；

(3)、当 $△ O A B$ 的面积为9时，求一次函数 $y = m x + n$ 的表达式．

查看试题解析
13. 近年来，市民交通安全意识逐步增强，头盔需求量增大．某商店购进甲、乙两种头盔，已知购买甲种头盔20只，乙种头盔30只，共花费2920元，甲种头盔的单价比乙种头盔的单价高11元．

(1)、甲、乙两种头盔的单价各是多少元？

(2)、商店决定再次购进甲、乙两种头盔共40只，正好赶上厂家进行促销活动，促销方式如下：甲种头盔按单价的八折出售，乙种头盔每只降价6元出售．如果此次购买甲种头盔的数量不低于乙种头盔数量的一半，那么应购买多少只甲种头盔，使此次购买头盔的总费用最小？最小费用是多少元？

查看试题解析
14. 如图，一次函数 $y = k x + \frac{9}{4}$ （ $k$ 为常数， $k \neq 0$ ）的图象与反比例函数 $y = \frac{m}{x} (m$ 为常数， $m \neq 0)$ 的图象在第一象限交于点 $A (1 ， n)$ ，与 $x$ 轴交于点 $B (- 3 ， 0)$ ．

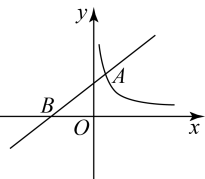(1)、求一次函数和反比例函数的解析式．

(2)、点 $P$ 在 $x$ 轴上， $△ A B P$ 是以 $A B$ 为腰的等腰三角形，请直接写出点 $P$ 的坐标．

查看试题解析
15. 如图，一次函数 $y = k x + b$ 的图像与反比例函数 $y = \frac{m}{x}$ 的图像相交于 $A (- 1 ， 4)$ ， $B (a ， - 1)$ 两点．

(1)、求反比例函数和一次函数的表达式；

(2)、点 $p (n ， 0)$ 在x轴负半轴上，连接AP，过点B作 $B Q ∥ A P$ ，交 $y = \frac{m}{x}$ 的图像于点Q，连接PQ．当 $B Q = A P$ 时，若四边形APQB的面积为36，求n的值．

查看试题解析
16. 已知抛物线 $y = a x^{2} + b x + 4$ 与 $x$ 轴相交于点 $A (1 ， 0)$ ， $B (4 ， 0)$ ，与 $y$ 轴相交于点 $C$ ．

(1)、求抛物线的表达式；

(2)、如图1，点 $P$ 是抛物线的对称轴 $l$ 上的一个动点，当 $△ P A C$ 的周长最小时，求 $\frac{P A}{P C}$ 的值；

(3)、如图2，取线段 $O C$ 的中点 $D$ ，在抛物线上是否存在点 $Q$ ，使 $t a n ∠ Q D B = \frac{1}{2}$ ？若存在，求出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析
17. 如图，二次函数 $y = - x^{2} + 4 x$ 的图象与 $x$ 轴的正半轴交于点A，经过点A的直线与该函数图象交于点 $B (1 ， 3)$ ，与 $y$ 轴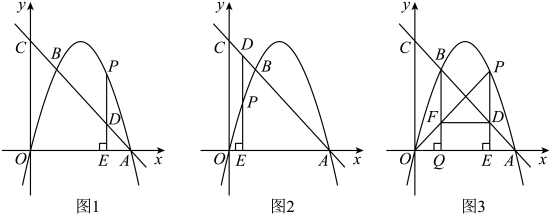交于点C．

(1)、求直线 $A B$ 的函数表达式及点C的坐标；

(2)、点 $P$ 是第一象限内二次函数图象上的一个动点，过点 $P$ 作直线 $P E ⊥ x$ 轴于点 $E$ ，与直线 $A B$ 交于点D，设点 $P$ 的横坐标为 $m$ ．
①当 $P D = \frac{1}{2} O C$ 时，求 $m$ 的值；

②当点 $P$ 在直线 $A B$ 上方时，连接 $O P$ ，过点 $B$ 作 $B Q ⊥ x$ 轴于点 $Q$ ， $B Q$ 与 $O P$ 交于点 $F$ ，连接 $D F$ ．设四边形 $F Q E D$ 的面积为 $S$ ，求 $S$ 关于 $m$ 的函数表达式，并求出S的最大值．

查看试题解析

18. 某移动公司推出A，B两种电话计费方式．

计费方式	月使用费/元	主叫限定时间/min	主叫超时费/（元/min）	被叫
A	$78$	$200$	$0.25$	免费
B	$108$	$500$	$0.19$	免费

(1)、设一个月内用移动电话主叫时间为tmin，根据上表，分别写出在不同时间范围内，方式A，方式B的计费金额关于t的函数解析式；

(2)、若你预计每月主叫时间为350min，你将选择A，B哪种计费方式，并说明理由；

(3)、请你根据月主叫时间t的不同范围，直接写出最省钱的计费方式．

查看试题解析

19. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c$ 与x轴交于 $B 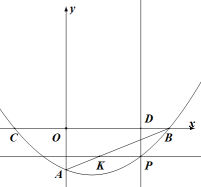(4 ， 0)$ ， $C (- 2 ， 0)$ 两点．与y轴交于点 $A (0 ， - 2)$ ．

(1)、求该抛物线的函数表达式；

(2)、若点P是直线 $A B$ 下方抛物线上的一动点，过点P作x轴的平行线交 $A B$ 于点K，过点P作y轴的平行线交x轴于点D，求与 $\frac{1}{2} P K + P D$ 的最大值及此时点P的坐标；

(3)、在抛物线的对称轴上是否存在一点M，使得 $△ M A B$ 是以 $A B$ 为一条直角边的直角三角形：若存在，请求出点M的坐标，若不存在，请说明理由．

查看试题解析
20. 如图，抛物线 $y = a x^{2} + b x + 5$ 与 $x$ 轴交于 $A ， B$ 两点，与 $y$ 轴交于点 $C ， A B = 4$ ．抛物线的对称轴 $x = 3$ 与经过点 $A$ 的直线 $y = k x - 1$ 交于点 $D$ ，与 $x$ 轴交于点 $E$ ．

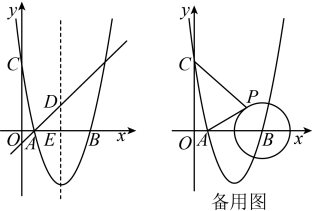(1)、求直线 $A D$ 及抛物线的表达式；

(2)、在抛物线上是否存在点 $M$ ，使得 $△ A D M$ 是以 $A D$ 为直角边的直角三角形?若存在，求出所有点 $M$ 的坐标；若不存在，请说明理由；

(3)、以点 $B$ 为圆心，画半径为2的圆，点 $P$ 为 $⊙ B$ 上一个动点，请求出 $P C + \frac{1}{2} P A$ 的最小值．

查看试题解析
21. 某动力科学研究院实验基地内装有一段笔直的轨道 $A B$ ，长度为 $1 m$ 的金属滑块在上面做往返滑动．如图，滑块首先沿 $A B$ 方向从左向右匀速滑动，滑动速度为 $9 m / s$ ，滑动开始前滑块左端与点 $A$ 重合，当滑块右端到达点 $B$ 时，滑块停顿 $2 s$ ，然后再以小于 $9 m / s$ 的速度匀速返回，直到滑块的左端与点 $A$ 重合，滑动停止．设时间为 $t (s)$ 时，滑块左端离点 $A$ 的距离为 $l_{1} (m)$ ，右端离点 $B$ 的距离为 $l_{2} (m)$ ，记 $d = l_{1} - l_{2} ， d$ 与 $t$ 具有函数关系．已知滑块在从左向右滑动过程中，当 $t = 4.5 s$ 和 $5.5 s$ 时，与之对应的 $d$ 的两个值互为相反数；滑块从点 $A$ 出发到最后返回点 $A$ ，整个过程总用时 $27 s$ （含停顿时间）．请你根据所给条件解决下列问题：

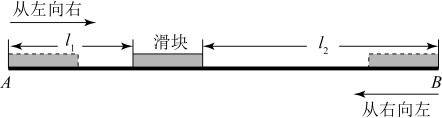(1)、滑块从点 $A$ 到点 $B$ 的滑动过程中， $d$ 的值；（填“由负到正”或“由正到负”）

(2)、滑块从点 $B$ 到点 $A$ 的滑动过程中，求 $d$ 与 $t$ 的函数表达式；

(3)、在整个往返过程中，若 $d = 18$ ，求 $t$ 的值．

查看试题解析
22. 如图，二次函数 $y = x^{2} + b x + c$ 的图象交 $x$ 轴于点 $A ， B$ ，交 $y$ 轴于点 $C$ ，点 $B$ 的坐标为 $(1 ， 0)$ ，对称轴是直线 $x = - 1$ ，点 $P$ 是 $x$ 轴上一动点， $P M ⊥ x$ 轴，交直线 $A C$ 于点 $M$ ，交抛物线于点 $N$ ．

(1)、求这个二次函数的解析式．

(2)、若点 $P$ 在线段 $A O$ 上运动（点 $P$ 与点 $A$ 、点 $O$ 不重合），求四边形 $A B C N$ 面积的最大值，并求出此时点 $P$ 的坐标．

(3)、若点 $P$ 在 $x$ 轴上运动，则在 $y$ 轴上是否存在点 $Q$ ，使以 $M$ 、 $N 、 C 、 Q$ 为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析
23. 如图1，抛物线 $y = a x^{2} + b x + 3$ （ $a \neq 0$ ）与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ．

(1)、求抛物线的解析式；

(2)、点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；

(3)、如图2，抛物线顶点为D，对称轴与x轴交于点E，过点 $K (1 ， 3)$ 的直线（直线 $K D$ 除外）与抛物线交于G，H两点，直线 $D G$ ， $D H$ 分别交x轴于点M，N．试探究 $E M \cdot E N$ 是否为定值，若是，求出该定值；若不是，说明理由．

查看试题解析

	$A$ 超市	$B$ 超市
优惠方案	所有商品按八折出售	购物金额每满 $100$ 元返 $30$ 元

日需求量n	$13$	$14$	$15$	$16$	$17$	$18$
天数	1	1	2	4	1	1

时间t/s	0	10	20	30	40
油温y/ $° C$	10	30	50	70	90