2023年中考数学真题分类汇编(全国版):一次方程(2)
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 一次函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若直线(是常数,)经过第一、第三象限,则的值可为( )A、 B、 C、 D、23. 如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 已知点在同一个函数图象上,则这个函数图象可能是( )A、
4. 已知点在同一个函数图象上,则这个函数图象可能是( )A、 B、
B、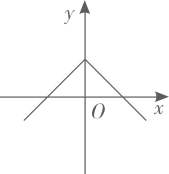 C、
C、 D、
D、 5. 在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( )
5. 在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( ) A、 B、 C、 D、6. 下列各点在函数图象上的是( )A、 B、 C、 D、7. 如图1,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论错误的是( )
A、 B、 C、 D、6. 下列各点在函数图象上的是( )A、 B、 C、 D、7. 如图1,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论错误的是( ) A、小亮从家到羽毛球馆用了分钟 B、小亮从羽毛球馆到报亭平均每分钟走米 C、报亭到小亮家的距离是米 D、小亮打羽毛球的时间是分钟8. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限9. 如图5,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,C、D是半径为1的上两动点,且 , P为弦CD的中点.当C、D两点在圆上运动时,面积的最大值是( )
A、小亮从家到羽毛球馆用了分钟 B、小亮从羽毛球馆到报亭平均每分钟走米 C、报亭到小亮家的距离是米 D、小亮打羽毛球的时间是分钟8. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限9. 如图5,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,C、D是半径为1的上两动点,且 , P为弦CD的中点.当C、D两点在圆上运动时,面积的最大值是( )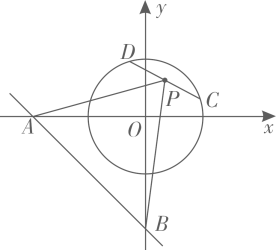 A、8 B、6 C、4 D、3
A、8 B、6 C、4 D、3二、填空题
-
10. 已知一次函数的图象经过点和 , 则 .11. 一个函数过点 , 且随增大而增大,请写出一个符合上述条件的函数解析式 .12. 我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”如图是善行者与不善行者行走路程(单位:步)关于善行者的行走时间的函数图象,则两图象交点的纵坐标是 .
 13. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .
13. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .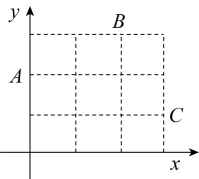
三、解答题
-
14. 如图,抛物线与x轴交于 , 两点,与轴交于点 .
 (1)、求抛物线解析式及 , 两点坐标;(2)、以 , , , 为顶点的四边形是平行四边形,求点坐标;(3)、该抛物线对称轴上是否存在点 , 使得 , 若存在,求出点的坐标;若不存在,请说明理由.
(1)、求抛物线解析式及 , 两点坐标;(2)、以 , , , 为顶点的四边形是平行四边形,求点坐标;(3)、该抛物线对称轴上是否存在点 , 使得 , 若存在,求出点的坐标;若不存在,请说明理由.四、综合题
-
15. 已知甲,乙两地相距 , 一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距 , 货车继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离与货车行驶时间之间的函数图象,结合图象回答下列问题:
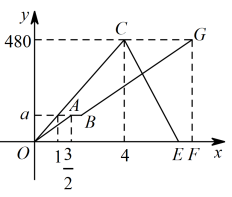 (1)、图中的值是;(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离与行驶时间之间的函数关系式;(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距 .16. 如图,抛物线与轴交于两点,交轴于点 .
(1)、图中的值是;(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离与行驶时间之间的函数关系式;(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距 .16. 如图,抛物线与轴交于两点,交轴于点 .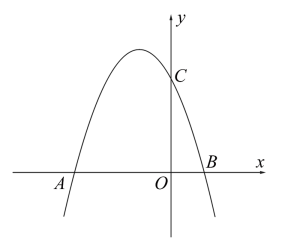 (1)、求抛物线的解析式.(2)、拋物线上是否存在一点 , 使得 , 若存在,请直接写出点的坐标;若不存在,请说明理由.17. 如图所示,一次函数与反比例函数相交于点A和点 .
(1)、求抛物线的解析式.(2)、拋物线上是否存在一点 , 使得 , 若存在,请直接写出点的坐标;若不存在,请说明理由.17. 如图所示,一次函数与反比例函数相交于点A和点 .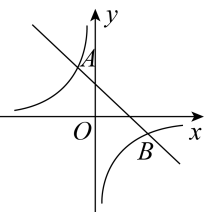 (1)、求m的值和反比例函数解析式;(2)、当时,求x的取值范围.18. 甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和与甲组挖掘时间x(天)之间的关系如图所示.
(1)、求m的值和反比例函数解析式;(2)、当时,求x的取值范围.18. 甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和与甲组挖掘时间x(天)之间的关系如图所示. (1)、甲组比乙组多挖掘了天.(2)、求乙组停工后y关于x的函数解析式,并写出自变量x的取值范围.(3)、当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组己停工的天数.19. 随着科技的发展,扫地机器人已广泛应用于生活中。某公司推出一款新型扫地机器人,经统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化.设该产品2022年第(为整数)个月每台的销售价格为(单位:元),与的函数关系如图所示(图中ABC为一折线).
(1)、甲组比乙组多挖掘了天.(2)、求乙组停工后y关于x的函数解析式,并写出自变量x的取值范围.(3)、当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组己停工的天数.19. 随着科技的发展,扫地机器人已广泛应用于生活中。某公司推出一款新型扫地机器人,经统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化.设该产品2022年第(为整数)个月每台的销售价格为(单位:元),与的函数关系如图所示(图中ABC为一折线).

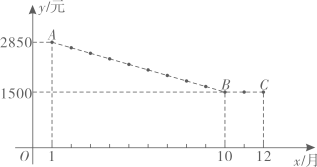 (1)、当1≤≤10时,求每台的销售价格与之间的函数关系式;(2)、设该产品2022年第个月的销售数量为(单位:万台),与的关系可以用来描述.求哪个月的销售收入最多,最多为多少万元?
(1)、当1≤≤10时,求每台的销售价格与之间的函数关系式;(2)、设该产品2022年第个月的销售数量为(单位:万台),与的关系可以用来描述.求哪个月的销售收入最多,最多为多少万元?(销售收入=每台的销售价格销售数量)
20. 经验表明,树在一定的成长阶段,其胸径树的主干在地面以上处的直径越大,树就越高通过对某种树进行测量研究,发现这种树的树高是其胸径的一次函数已知这种树的胸径为时,树高为;这种铜的胸径为时,树高为 .(1)、求与之间的函数表达式;(2)、当这种树的胸径为时,其树高是多少?21. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.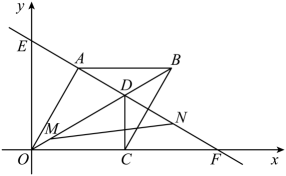 (1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.22. 如图,在平面直角坐标系中,抛物线交轴于点 , 直线交抛物线于B,C两点(点B在点的左侧),交轴于点 , 交轴于点.
(1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.22. 如图,在平面直角坐标系中,抛物线交轴于点 , 直线交抛物线于B,C两点(点B在点的左侧),交轴于点 , 交轴于点. (1)、求点D,E,C的坐标;(2)、F是线段OE上一点 , 连接AF,DF,CF,且.
(1)、求点D,E,C的坐标;(2)、F是线段OE上一点 , 连接AF,DF,CF,且.①求证:是直角三角形;
②的平分线FK交线段DC于点K,P是直线BC上方抛物线上一动点,当时,求点的坐标.
23. 综合运用如图1,在平面直角坐标系中,正方形的顶点A在轴的正半轴上,如图2,将正方形绕点逆时针旋转,旋转角为 , 交直线于点 , 交轴于点 .
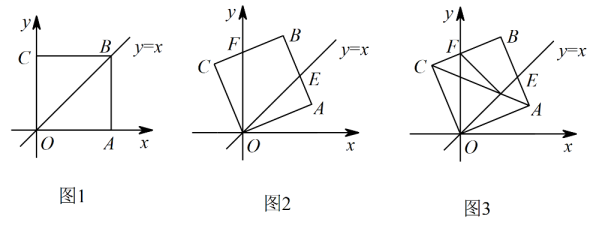 (1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.24. 某校组织师生参加夏令营活动,现准备租用A、B两型客车(每种型号的客车至少租用一辆).A型车每辆租金500元,B型车每辆租金600元.若5辆A型和2辆B型车坐满后共载客310人;3辆A型和4辆B型车坐满后共载客340人.(1)、每辆A型车、B型车坐满后各载客多少人?(2)、若该校计划租用A型和B型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)、在这次活动中,学校除租用A、B两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t为何值时两车相距25千米.
(1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.24. 某校组织师生参加夏令营活动,现准备租用A、B两型客车(每种型号的客车至少租用一辆).A型车每辆租金500元,B型车每辆租金600元.若5辆A型和2辆B型车坐满后共载客310人;3辆A型和4辆B型车坐满后共载客340人.(1)、每辆A型车、B型车坐满后各载客多少人?(2)、若该校计划租用A型和B型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)、在这次活动中,学校除租用A、B两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t为何值时两车相距25千米.
 25. 已知:y关于x的函数 .
25. 已知:y关于x的函数 . (1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .
(1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,-是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
-