2023年中考数学真题分类汇编(全国版):平面直角坐标系
试卷更新日期:2023-07-23 类型:二轮复习
一、选择题
-
1. 在直角坐标系中,把点先向右平移1个单位,再向上平移3个单位得到点 . 若点的横坐标和纵坐标相等,则( )A、2 B、3 C、4 D、52. 在平面直角坐标系中,将点先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )A、 B、 C、 D、3. 如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“車”所在位留的坐标为 , 则“炮”所在位置的坐标为( ).
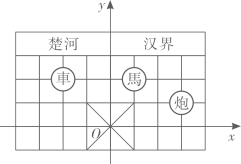 A、 B、 C、 D、4. 如图,两盘灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B',则关于点A',B'的位置描述正确是( )
A、 B、 C、 D、4. 如图,两盘灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B',则关于点A',B'的位置描述正确是( ) A、关于轴对称 B、关于轴对称 C、关于原点对称 D、关于直线对称5. 已知,二次数的图象如图所示,则点所在的象限是( )
A、关于轴对称 B、关于轴对称 C、关于原点对称 D、关于直线对称5. 已知,二次数的图象如图所示,则点所在的象限是( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在平面直角坐标系中,菱形的边长为 , 点在轴的正半轴上,且 , 将菱形绕原点逆时针方向旋转 , 得到四边形点与点重合 , 则点的坐标是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在平面直角坐标系中,菱形的边长为 , 点在轴的正半轴上,且 , 将菱形绕原点逆时针方向旋转 , 得到四边形点与点重合 , 则点的坐标是( )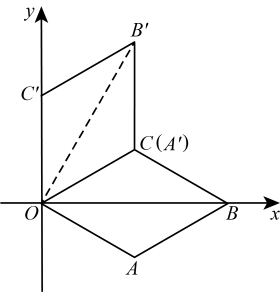 A、 B、 C、 D、7. 象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( )
A、 B、 C、 D、7. 象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( ) A、y=x+1 B、y=x-1 C、y=2x+1 D、y=2x-18. 如图,直线分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转得到△CAD,则点B的对应点D的坐标是( )
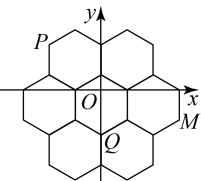
A、y=x+1 B、y=x-1 C、y=2x+1 D、y=2x-18. 如图,直线分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转得到△CAD,则点B的对应点D的坐标是( ) A、(2,5) B、(3,5) C、(5,2) D、( , 2)9. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为 , 则点的坐标为( )
A、(2,5) B、(3,5) C、(5,2) D、( , 2)9. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为 , 则点的坐标为( )
 A、 B、 C、 D、10. 如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A、 B、 C、 D、10. 如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( ) A、 B、 C、 D、11. 在平面直角坐标系中,点P(-1,m2+1)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P为位似中心作正方形 , 正方形 , 按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为 , , 则顶点的坐标为( )
A、 B、 C、 D、11. 在平面直角坐标系中,点P(-1,m2+1)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P为位似中心作正方形 , 正方形 , 按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为 , , 则顶点的坐标为( )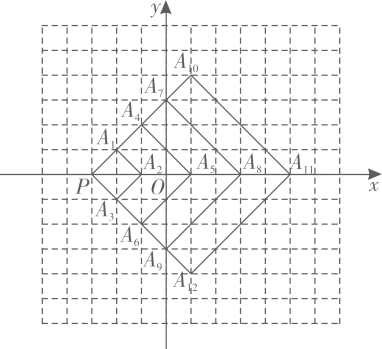 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 在平面直角坐标系中,点所在象限是第象限.14. 在平面直角坐标系中,若点与点关于原点对称,则的值是 .15. 如图,已知点 , 点B在y轴正半轴上,将线段绕点A顺时针旋转到线段 , 若点C的坐标为 , 则 .
 16. 在平面直角坐标系中,将点向左平移5个单位长度,得到点 , 则点的坐标是 .17. 若点在第四象限,则m的取值范围是 .18. 如图,是贵阳市城市轨道交通运营部分示意图,以喷水池为原点,分别以正东、正北方向为轴、轴的正方向建立平面直角坐标系,若贵阳北站的坐标是 , 则龙洞堡机场的坐标是 .
16. 在平面直角坐标系中,将点向左平移5个单位长度,得到点 , 则点的坐标是 .17. 若点在第四象限,则m的取值范围是 .18. 如图,是贵阳市城市轨道交通运营部分示意图,以喷水池为原点,分别以正东、正北方向为轴、轴的正方向建立平面直角坐标系,若贵阳北站的坐标是 , 则龙洞堡机场的坐标是 . 19. 如图,一束光线从点出发,经过y轴上的点反射后经过点 , 则的值是 .
19. 如图,一束光线从点出发,经过y轴上的点反射后经过点 , 则的值是 . 20. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)
20. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)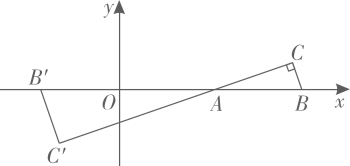 21. 如图,在平面直角坐标系中,已知点 , 点 , 点在轴上,且点在点右方,连接 , , 若 , 则点的坐标为 .
21. 如图,在平面直角坐标系中,已知点 , 点 , 点在轴上,且点在点右方,连接 , , 若 , 则点的坐标为 . 22. 在平面直角坐标系中有五个点,分别是 , , , , , 从中任选一个点恰好在第一象限的概率是 .23. 银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如图是一片银杏叶标本,叶片上两点B,C的坐标分别为 , 将银杏叶绕原点顺时针旋转后,叶柄上点A对应点的坐标为 .
22. 在平面直角坐标系中有五个点,分别是 , , , , , 从中任选一个点恰好在第一象限的概率是 .23. 银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如图是一片银杏叶标本,叶片上两点B,C的坐标分别为 , 将银杏叶绕原点顺时针旋转后,叶柄上点A对应点的坐标为 . 24. 画一条水平数轴,以原点为圆心,过数轴上的每一刻度点画同心圆,过原点按逆时针方向依次画出与正半轴的角度分别为的射线,这样就建立了“圆”坐标系.如图,在建立的“圆”坐标系内,我们可以将点的坐标分别表示为、 , 则点的坐标可以表示为.
24. 画一条水平数轴,以原点为圆心,过数轴上的每一刻度点画同心圆,过原点按逆时针方向依次画出与正半轴的角度分别为的射线,这样就建立了“圆”坐标系.如图,在建立的“圆”坐标系内,我们可以将点的坐标分别表示为、 , 则点的坐标可以表示为.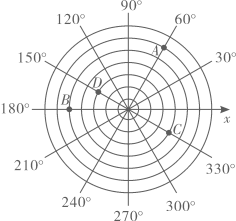 25. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:;;;;…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对: .
25. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:;;;;…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对: . 26. 在平面直角坐标系中,为等边三角形,点A的坐标为 . 把按如图所示的方式放置,并将进行变换:第一次变换将绕着原点O顺时针旋转 , 同时边长扩大为边长的2倍,得到;第二次旋转将绕着原点O顺时针旋转 , 同时边长扩大为 , 边长的2倍,得到 , ….依次类推,得到 , 则的边长为 , 点的坐标为 .
26. 在平面直角坐标系中,为等边三角形,点A的坐标为 . 把按如图所示的方式放置,并将进行变换:第一次变换将绕着原点O顺时针旋转 , 同时边长扩大为边长的2倍,得到;第二次旋转将绕着原点O顺时针旋转 , 同时边长扩大为 , 边长的2倍,得到 , ….依次类推,得到 , 则的边长为 , 点的坐标为 .
三、综合题
-
27. 如图,在平面直角坐标系中,抛物线上有两点 , 其中点的横坐标为 , 点的横坐标为 , 抛物线过点 . 过作轴交抛物线另一点为点 . 以长为边向上构造矩形 .
 (1)、求抛物线的解析式;(2)、将矩形向左平移个单位,向下平移个单位得到矩形 , 点的对应点落在抛物线上.
(1)、求抛物线的解析式;(2)、将矩形向左平移个单位,向下平移个单位得到矩形 , 点的对应点落在抛物线上.①求关于的函数关系式,并直接写出自变量的取值范围;
②直线交抛物线于点 , 交抛物线于点 . 当点为线段的中点时,求的值;
③抛物线与边分别相交于点 , 点在抛物线的对称轴同侧,当时,求点的坐标.