2023年中考数学真题分类汇编（全国版）：一元一次方程

试卷更新日期：2023-07-22 类型：二轮复习

进入出卷网下载

一、选择题

1. 《孙子算经》是中国古代重要的数学著作，是《算经十书》之一.书中记载了这样一个题目：今有木，不知长短.引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何？其大意是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺.问木长多少尺？设木长x尺，则可列方程为（）

A、 $\frac{1}{2} (x + 4.5) = x - 1$ B、 $\frac{1}{2} (x + 4.5) = x + 1$ C、 $\frac{1}{2} (x + 1) = x - 4.5$ D、 $\frac{1}{2} (x - 1) = x + 4.5$

查看试题解析
2. 《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数鸡价各几何？译文：今有人合伙买鸡，每人出9钱，会多出11钱；每人出6钱，又差16钱．问人数、买鸡的钱数各是多少？设人数为x，可列方程为（）

A、 $9 x + 11 = 6 x + 16$ B、 $9 x - 11 = 6 x - 16$ C、 $9 x + 11 = 6 x - 16$ D、 $9 x - 11 = 6 x + 16$

查看试题解析
3. 《孙子算经》中有这样一道题，大意为：今有100头鹿，每户分一头鹿后，还有剩余，将剩下的鹿按每3户共分一头，恰好分完，问：有多少户人家？若设有x户人家，则下列方程正确的是（）

A、 $x + \frac{1}{3} = 100$ B、 $3 x + 1 = 100$ C、 $x + \frac{1}{3} x = 100$ D、 $\frac{x + 1}{3} = 100$

查看试题解析
4. 我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一，书中记载一道问题：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之？”题意是：快马每天走240里，慢马每天走150里，慢马先走12天，试问快马几天可以追上慢马？若设快马x天可以追上慢马，则下列方程正确的是（）

A、 $240 x + 150 x = 150 \times 12$ B、 $240 x - 150 x = 240 \times 12$ C、 $240 x + 150 x = 240 \times 12$ D、 $240 x - 150 x = 150 \times 12$

查看试题解析
5. 《孙子算经》记载：“今有木，不知长短．引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？”（尺、寸是长度单位，1尺＝10寸）．意思是，现有一根长木，不知道其长短．用一根绳子去度量长木，绳子还剩余4.5尺；将绳子对折再度量长木，长木还剩余1尺．问长木长多少？设长木长为x尺，则可列方程为（）

A、 $\frac{1}{2} (x + 4.5) = x - 1$ B、 $\frac{1}{2} (x + 4.5) = x + 1$ C、 $\frac{1}{2} (x - 4.5) = x + 1$ D、 $\frac{1}{2} (x - 4.5) = x - 1$

查看试题解析
6. 元朝朱世杰所著的《算学启蒙》中，记载了这样一道题：良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之？其大意是：快马每天行240里，慢马每天行150里，慢马先行12天，快马几天可追上慢马？若设快马 $x$ 天可追上慢马，由题意得（）

A、 $\frac{x}{240} = \frac{x + 12}{150}$ B、 $\frac{x}{240} = \frac{x}{150} - 12$ C、 $240 (x - 12) = 150 x$ D、 $240 x = 150 (x + 12)$

查看试题解析

二、填空题

7. 《九章算术》中记载了一道数学问题，其译文为：有人合伙买羊，每人出5钱，还缺45钱；每人出7钱，还缺3钱．问合伙人数是多少？为解决此问题，设合伙人数为x人，可列方程为．

查看试题解析
8. 小伟用撬棍撬动一块大石头，已知阻力和阻力臂分别为1000N和0.6m，当动力臂由1.5m增加到2m时，撬动这块石头可以节省N的力．（杜杆原理：阻力 $\times$ 阻力臂 $＝$ 动力 $\times$ 动力臂）

查看试题解析
9. 古代中国的数学专著《九章算术》中有一题：“今有生丝三十斤，千之，耗三斤十二两．今有干丝一十二斤，问生丝几何？“意思是：“今有生丝30斤，干燥后耗损3斤12两(古代中国1斤等于16两)．今有干丝12斤，问原有生丝多少？”则原有生丝为斤．

查看试题解析

三、解答题

10. 小红在一家文具店买了一种大笔记本 $4$ 个和一种小笔记本 $6$ 个，共用了 $62$ 元 $.$ 已知她买的这种大笔记本的单价比这种小笔记本的单价多 $3$ 元，求该文具店中这种大笔记本的单价．

查看试题解析
11. 某校组织七年级学生到江姐故里研学旅行，租用同型号客车4辆，还剩30人没有座位；租用5辆，还空10个座位．求该客车的载客量．

查看试题解析

四、综合题

12. 1号探测气球从海拔10m处出发，以1m/min的速度竖直上升．与此同时，2号探测气球从海拔20m处出发，以am/min的速度竖直上升．两个气球都上升了1h.1号、2号气球所在位置的海拔 $y_{1}$ ， $y_{2}$ （单位：m）与上升时间x（单位：min）的函数关系如图所示．请根据图象回答下列问题：

(1)、a= ， b；

(2)、请分别求出 $y_{1}$ ， $y_{2}$ 与x的函数关系式；

(3)、当上升多长时间时，两个气球的海拔竖直高度差为5m？

查看试题解析
13. 某健身器材专卖店推出两种优惠活动，并规定购物时只能选择其中一种．
活动一：所购商品按原价打八折；
活动二：所购商品按原价每满300元减80元．（如：所购商品原价为300元，可减80元，需付款220元；所购商品原价为770元，可减160元，需付款610元）

(1)、购买一件原价为450元的健身器材时，选择哪种活动更合算？请说明理由．

(2)、购买一件原价在500元以下的健身器材时，若选择活动一和选择活动二的付款金额相等，求一件这种健身器材的原价．

(3)、购买一件原价在900元以下的健身器材时，原价在什么范围内，选择活动二比选择活动一更合算？设一件这种健身器材的原价为a元，请直接写出a的取值范围．

查看试题解析
14.

(1)、解不等式组： ${\begin{array}{l} 2 x < 16 ① \\ 3 x > 2 x + 3 ② \end{array}$

(2)、金秋时节，新疆瓜果飘香．某水果店A种水果每千克5元，B种水果每千克8元，小明买了A、B两种水果共7千克花了41元．A、B两种水果各买了多少千克？

查看试题解析
15. 对于任意实数a，b，定义一种新运算： $a ※ b = {\begin{array}{l} a - b & (a \geq 2 b) \\ a + b - 6 & (a < 2 b) \end{array}$ ，例如： $3 ※ 1 = 3 - 1 = 2$ ， $5 ※ 4 = 5 + 4 - 6 = 3$ ．根据上面的材料，请完成下列问题：

(1)、 $4 ※ 3 =$ ， $(- 1) ※ (- 3) =$ ；

(2)、若 $(3 x + 2) ※ (x - 1) = 5$ ，求x的值．

查看试题解析
16. 某中学组织学生研学，原计划租用可坐乘客 $45$ 人的 $A$ 种客车若干辆，则有 $30$ 人没有座位；若租用可坐乘客 $60$ 人的 $B$ 种客车，则可少租 $6$ 辆，且恰好坐满．

(1)、求原计划租用 $A$ 种客车多少辆？这次研学去了多少人？

(2)、若该校计划租用 $A$ 、 $B$ 两种客车共 $25$ 辆，要求 $B$ 种客车不超过 $7$ 辆，且每人都有座位，则有哪几种租车方案？

(3)、在（2）的条件下，若 $A$ 种客车租金为每辆 $220$ 元， $B$ 种客车租金每辆 $300$ 元，应该怎样租车才最合算？

查看试题解析
17. 某公司不定期为员工购买某预制食品厂生产的杂酱面、牛肉面两种食品．

(1)、该公司花费3000元一次性购买了杂酱面、牛肉面共170份，此时杂酱面、牛肉面的价格分别为15元、20元，求购买两种食品各多少份？

(2)、由于公司员工人数和食品价格有所调整，现该公司分别花费1260元、1200元一次性购买杂酱面、牛肉面两种食品，已知购买杂酱面的份数比牛肉面的份数多 $50 ％$ ，每份杂酱面比每份牛肉面的价格少6元，求购买牛肉面多少份？

查看试题解析
18. 如图， $△ A B C$ 是边长为4的等边三角形，动点E，F分别以每秒1个单位长度的速度同时从点A出发，点E沿折线 $A \to B \to C$ 方向运动，点F沿折线 $A \to C \to B$ 方向运动，当两者相遇时停止运动．设运动时间为t秒，点E，F的距离为y．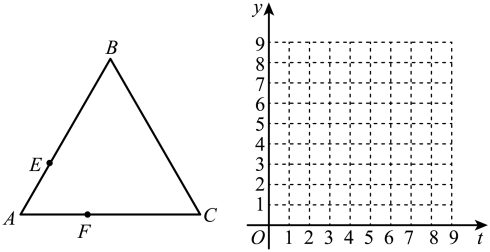

(1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围；

(2)、在给定的平面直角坐标系中画出这个函数的图象，并写出该函数的一条性质；

(3)、结合函数图象，写出点E，F相距3个单位长度时t的值．

查看试题解析
19. 某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召，积极扩大粮食生产规模，计划用基地的甲、乙两区农田进行油菜试种．甲区的农田比乙区的农田多10000亩，甲区农田的 $80 %$ 和乙区全部农田均适宜试种，且两区适宜试种农田的面积刚好相同．

(1)、求甲、乙两区各有农田多少亩？

(2)、在甲、乙两区适宜试种的农田全部种上油菜后，为加强油菜的虫害治理，基地派出一批性能相同的无人机，对试种农田喷洒除虫药，由于两区地势差别，派往乙区的无人机架次是甲区的1.2倍（每架次无人机喷洒时间相同），喷洒任务完成后，发现派往甲区的每架次无人机比乙区的平均多喷洒 $\frac{50}{3}$ 亩，求派往甲区每架次无人机平均喷洒多少亩？

查看试题解析

20. 目前，我市对市区居民用气户的燃气收费，以户为基础、年为计算周期设定了如下表的三个气量阶梯：

阶梯	年用气量	销售价格	备注
第一阶梯	$0 ~ 400$ $m^{3}$ （含400）的部分	2.67元 $/ m^{3}$	若家庭人口超过4人的，每增加1人，第一、二阶梯年用气量的上限分别增加 $100 m^{3} 、 200 m^{3}$ .
第二阶梯	$400 ~ 1200 m^{3}$ （含1200）的部分	3.15元 $/ m^{3}$
第三阶梯	$1200 m^{3}$ 以上的部分	3.63元 $/ m^{3}$

(1)、一户家庭人口为3人，年用气量为

200 m^{3}

，则该年此户需缴纳燃气费用为元；

(2)、一户家庭人口不超过4人，年用气量为

x m^{3} (x > 1200)

，该年此户需缴纳燃气费用为

y

元，求

y

与

x

的函数表达式；

(3)、甲户家庭人口为3人，乙户家庭人口为5人，某年甲户、乙户缴纳的燃气费用均为3855元，求该年乙户比甲户多用多少立方米的燃气？（结果精确到

1 m^{3}

）

查看试题解析