安徽省安庆潜山市2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-21 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $(2022 ， - 2023)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 从数学角度看下列四幅图片有一个与众不同，该图片是（）

A、 B、 C、 D、

查看试题解析
3. 对于命题“若 $a^{2} > b^{2}$ ，则 $a > b$ ”，下面四组关于a，b的值中，能说明这个命题的逆命题是假命题的是（）

A、 $a = 3 ， b = 2$ B、 $a = 2 ， b = - 3$ C、 $a = - 2 ， b = - 1$ D、 $a = 2 ， b = - 1$

查看试题解析
4. 下列方程组中，有无数组解的是（）

A、 ${\begin{array}{l} 2 x - y = - 2 \\ x - 2 y = - 1 \end{array}$ B、 ${\begin{array}{l} y = 3 x + 5 \\ y = 3 x - 2 \end{array}$ C、 ${\begin{array}{l} x - 4 y - 7 = 0 \\ 2 x - 8 y - 14 = 0 \end{array}$ D、 ${\begin{array}{l} y = x - 3 \\ y = 2 x - 3 \end{array}$

查看试题解析
5. 一次函数 $y = k x + b$ 的图象经过 $A (m ， 1) ， B (m + 4 ， 0)$ 两点，若点 $M (2 ， y_{1})$ 和点 $N (3 ， y_{2})$ 恰好也是该函数图象上的两点，则 $y_{1} ， y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、无法确定

查看试题解析
6. 如图，在 $△ A B C$ 中，E，F分别是 $A B$ ， $A C$ 上的点，且 $E F ∥ B C$ ， $A D$ 是 $∠ B A C$ 的平分线，分别交 $E F$ ， $B C$ 于点H，D，则 $∠ 1$ 、 $∠ 2$ 和 $∠ 3$ 之间的数量关系为（）

A、 $∠ 1 = ∠ 2 + ∠ 3$ B、 $∠ 1 = 2 ∠ 2 + ∠ 3$ C、 $∠ 1 + ∠ 2 = 2 ∠ 3$ D、 $∠ 1 + ∠ 3 = 2 ∠ 2$

查看试题解析
7. 若一次函数 $y = (m - 3) x - m + 2$ 的图象不经过第一象限，则m的取值范围（）

A、 $2 < m < 3$ B、 $2 \leq m \leq 3$ C、 $m \geq 2$ D、 $2 \leq m < 3$

查看试题解析
8. 如图，是一个 3×4 的网格（由 12 个小正方形组成，虚线交点称之格点）图中有一个三角形，三个顶点都在格点上，在网格中可以画出（）个与此三角形关于某直线对称的格点三角形.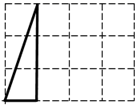

A、6 B、7 C、8 D、9

查看试题解析
9. 如图，在 $△ A B C$ 中， $A E$ 平分 $∠ B A C$ ， $E B ⊥ A B$ 且 $E A = E C$ ．以下判断正确的是（）

A、 $A C = 2 A E$ B、 $A C = 2 A B$ C、 $B C = 2 A B$ D、 $A B = 2 B E$

查看试题解析
10. 火车匀速通过隧道时，火车在隧道内的长度y（米）与火车行驶时间x（秒）之间的关系用图象描述如图所示，有下列结论：①火车的长度为150米；②火车的速度为30米/秒；③火车整体都在隧道内的时间为25秒；④隧道长度为750米．其中正确的结论是（）

A、①②③ B、②③④ C、①②③④ D、②④

查看试题解析

二、填空题

11. 函数y= $\frac{\sqrt{x + 1}}{x - 3}$ 中自变量x的取值范围是．

查看试题解析
12. 在平面直角坐标系中，将直线 $y = k x - 6$ 向右平移3个单位后恰好经过原点，则k的值为．

查看试题解析
13. 如图，在△ABC中， $∠ B = 74 °$ ，边AC的垂直平分线交 $B C$ 于点D，交 $A C$ 于点E，若 $A B ＋ B D = B C$ ，则 $∠ B A C$ 的度数为．

查看试题解析
14. 在平面直角坐标系中，已知点 $A (- 3 ， - 2)$ ， $B (1 ， - 1)$ ， $C (0 ， - 4)$ ．

(1)、直线 $y = a x + 3 a - 2$ （ $a$ 为常数）一定经过点；

(2)、若直线 $y = a x + 3 a - 2$ （ $a$ 为常数）与线段 $B C$ 有交点，则 $a$ 的取值范围．

查看试题解析

三、解答题

15. 已知 $△ A B C$ 在 $8 \times 8$ 方格中，位置如图所示，其中点A的坐标为 $(- 3 ， 1)$ ，点B的坐标为 $(- 2 ， 4)$ ．

(1)、写出点C的坐标；

(2)、 $△ A B C$ 经某种变换得到 $△ A^{'} B^{'} C^{'}$ ，其中点A对应点 $A^{'}$ 的坐标为 $(- 1 ， 2)$ ，点B对应点 $B^{'}$ 的坐标为 $(0 ， 5)$ ，请在图上标出点 $C^{'}$ ；

查看试题解析

16. 通过对函数的学习，我们积累了研究函数的经验，以下是探究函数

y = | x + 1 | - 2

的部分过程，请按要求完成下列各题：

x	…	$- 4$	$- 3$	$- 2$	$- 1$	0	1	2	3	4	…
y	…	1	0	a	$- 2$	$- 1$	0	1	2	3	…

(1)、表中a的值为；

(2)、在右边的坐标系中画出该函数图象；

(3)、结合图象，可知不等式

| x + 1 | - 2 \geq 0

的解集是．

查看试题解析

17. 如图， $△ A B C$ 和 $△ D E C$ 均为等边三角形．

(1)、找出与 $△ D A C$ 全等的三角形（不需要说明理由）；

(2)、若 $∠ A D B = 82 °$ ，求 $∠ D B E$ 的度数．

查看试题解析
18. 在 $△ A B C$ 中， $A B = C B$ ， $∠ A B C = 90 °$ ， F为 $A B$ 延长线上一点，点E在 $B C$ 上，且 $A E = C F$ ．

(1)、求证： $R t △ A B E ≌ R t △ C B F$ ；

(2)、若 $∠ C A E = 32 °$ ，求 $∠ A C F$ 度数．

查看试题解析
19. 一次函数 $y = k x + b$ 的自变量x的取值范围是 $- 4 \leq x \leq 2$ ，相应函数值的取值范围是 $1 \leq y \leq 4$ ，求这个函数的解析式．

查看试题解析
20. 如图， $∠ A B C = 100 °$ ．

(1)、用尺规作出 $∠ B$ 的角平分线 $B M$ 和线段 $B C$ 的垂直平分线 $G H$ （不写作法，保留作图痕迹）；

(2)、按下面要求画出图形： $B M$ 和 $G H$ 交于点 $D$ ， $G H$ 交 $B C$ 于点 $E$ ，连接 $C D$ 并延长，交 $A B$ 于点 $F$ ；

(3)、求证： $F D = 2 D E$ ．

查看试题解析
21. 如图，在平面直角坐标系xOy中，一次函数y＝k₁x＋b的图象与x轴交于点A（－3，0），与y轴交于点B ，且与正比例函数y＝kx的图象交点为C（3，4）．

(1)、求k值与一次函数y＝k₁x＋b的解析式；

(2)、在x轴上有一动点P ，求当PB+PC最小时P点坐标．

(3)、若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，请求出点D的坐标；

查看试题解析
22. 如图， $A E$ 与 $B D$ 相交于点C， $A C = E C$ ， $B C = D C$ ， $A B = 10 c m$ ，点P从点A出发，沿 $A \to B \to A$ 方向以 $2 c m / s$ 的速度运动，点Q从点D出发，沿 $D \to E$ 方向以 $1 c m / s$ 的速度运动，P、Q两点同时出发，当点P回到点A时，P、Q两点同时停止运动，设点P的运动时间为 $t (s)$ ．

(1)、求证： $A B ∥ D E$ ．

(2)、写出线段 $A P$ 的长（用含t的式子表示）．

(3)、连接 $P Q$ ，当线段 $P Q$ 经过点C时，求t的值．

查看试题解析
23. 为了响应国家退耕还林政策，某器材销售公司捐出五月份全部销售利润用于种树．已知该公司五月份只售出甲、乙、丙三种型号器材若干台，每种型号器材不少于8台，五月份支出包括这批器材进货款54万元和其他支出（含人员工资、杂项开支）共3.25万元．这三种器材的进价和售价如下表所示，人员工资 $y_{1}$ （万元）和杂项支出 $y_{2}$ （万元）分别与总销售量x（台）成一次函数关系（如图）．

型号
甲
乙
丙
进价（万元/台）
0.9
1.2
1.1
售价（万元/台）
1.2
1.6
1.3

(1)、直接写出： $y_{1}$ 与x之间的函数表达式为；五月份该公司的总销售量为台；

(2)、设公司五月份售出甲种型号器材t台，五月份总销售利润为W（万元），求W与t之间的函数表达式；

(3)、请推测该公司这次活动捐款金额的最大值．

查看试题解析

型号	甲	乙	丙
进价（万元/台）	0.9	1.2	1.1
售价（万元/台）	1.2	1.6	1.3