吉林省长春市绿园区2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-07-21 类型:期末考试
一、选择题(本大题共8小题,共24.0分。)
-
1. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 成人体内成熟的红细胞的平均直径一般为 , 数用科学记数法表示是( )A、 B、 C、 D、3. 若分式的值是 , 则的值是( )A、 B、 C、 D、或4. 已知正比例函数的图象过第二、四象限,则的取值范围是( )A、 B、 C、 D、5. 如图,在▱ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则BC的长为( )
 A、4cm B、5cm C、6cm D、8cm6. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、4cm B、5cm C、6cm D、8cm6. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )甲
乙
丙
丁
平均数
方差
A、甲 B、乙 C、丙 D、丁7. 如图,在菱形中,对角线与相交于点 , 且 , , 则菱形的高( )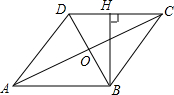 A、 B、 C、 D、8. 如图,在平面直角坐标系中,反比例函数在第一象限内的图象经过点和点 , 则的面积为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,反比例函数在第一象限内的图象经过点和点 , 则的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
9. 在一定条件下,若物体运动的路程米与时间秒的关系式为 , 则当时,该物体所经过的路程为 .10. 已知一次函数的图象经过点 , 且与直线的图象平行,则一次函数表达式为 .11. 若点在反比例函数的图象上,则代数式的值为 .12. 如图,在▱ABCD中,E为边BC上一点,以AE为边作矩形AEFG.若∠BAE=40°,∠CEF=15°,则∠D的大小为度.
 13. 如图,正方形ABCD的边长为1,点E在BC的延长线上.如果BE=BD,那么CE=
13. 如图,正方形ABCD的边长为1,点E在BC的延长线上.如果BE=BD,那么CE=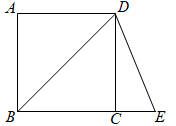 14. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与轴负半轴相交,则关于的不等式的解集为 .
14. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与轴负半轴相交,则关于的不等式的解集为 .
三、解答题(本大题共10小题,共78.0分。)
-
15. 计算: .16. 先化简,再求值: , 其中 .17. (列方程解应用题)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本,求A和B两种图书的单价分别为多少元?18. 如图,在四边形中, , , 为边上一点,且 ,
连结 .
 (1)、求证:四边形是矩形;(2)、若平分 , , , 求的长,19. 某商场服装部为了调动营业员的积极性,决定实行日标管理,根据日标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售日标,商场服装部统计了每位营业员在某月的销售额单位:万元 , 数据如下:
(1)、求证:四边形是矩形;(2)、若平分 , , , 求的长,19. 某商场服装部为了调动营业员的积极性,决定实行日标管理,根据日标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售日标,商场服装部统计了每位营业员在某月的销售额单位:万元 , 数据如下:30 16 14 15 26 15 32 23 17 15 15 28 28 16 19 17 18 16 13 24 15 28 26 18 19 22 17 16 1932
整理上面的数据,得到下面两个不完整的统计表:
频数分布表:
组别
一
二
三
四
五
六
七
销售额
频数
数据分析表:
平均数
众数
中位数
请根据以上信息解答下列问题:
(1)、填空: , , ;;(2)、若将月销售额不低于万元确定为销售目标,则有位营业员可以获得奖励;(3)、若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.20. 图、图均为的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为线段、的端点均在格点上,只用无刻度的直尺,在给定的网格中按要求作图,使所画图形的顶点均在格点上,并回答问题.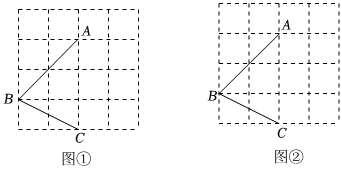 (1)、在图中画一个四边形 , 使四边形中的两组对角分别相等;(2)、在图中画一个四边形 , 使四边形中有一组对角相等,另一组对角不相等;(3)、四边形的面积是 .21. 李明驾车以千米小时的速度从甲地匀速开往乙地,行驶到服务区休息了一段时间后以另一速度继续匀速行驶,直至到达乙地.李明与乙地的距离千米与时间小时之间的函数关系图象如图所示.
(1)、在图中画一个四边形 , 使四边形中的两组对角分别相等;(2)、在图中画一个四边形 , 使四边形中有一组对角相等,另一组对角不相等;(3)、四边形的面积是 .21. 李明驾车以千米小时的速度从甲地匀速开往乙地,行驶到服务区休息了一段时间后以另一速度继续匀速行驶,直至到达乙地.李明与乙地的距离千米与时间小时之间的函数关系图象如图所示.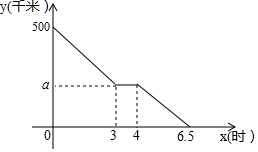 (1)、求的值;(2)、求李明从服务区到乙地与之间的函数关系式;(3)、求时李明驾车行驶的路程.22. 【感知】如图 , 在▱中,对角线、相交于点 , 过点的直线分别交边、于点、 , 易证:不需要证明;
(1)、求的值;(2)、求李明从服务区到乙地与之间的函数关系式;(3)、求时李明驾车行驶的路程.22. 【感知】如图 , 在▱中,对角线、相交于点 , 过点的直线分别交边、于点、 , 易证:不需要证明;
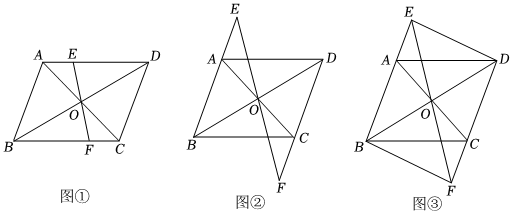 (1)、【探究】如图 , 在▱中,对角线、相交于点 , 过点的直线分别交边、的延长线于、 , 求证:;(2)、【应用】如图 , 在▱中,对角线、相交于点 , 过点的直线分别交边、的延长线于、 , 连接、 , 若 , 的面积为 , 则四边形的面积为 .23. 如图,在矩形中, , , 动点从点出发以每秒个单位长度的速度沿向终点匀速运动,同时动点从点出发以每秒个单位长度的速度沿折线向终点匀速运动,当点到达终点时,点也随之停止运动以、为邻边构造▱ , 设▱与矩形重叠部分的面积为 , 点的运动时间为秒 .
(1)、【探究】如图 , 在▱中,对角线、相交于点 , 过点的直线分别交边、的延长线于、 , 求证:;(2)、【应用】如图 , 在▱中,对角线、相交于点 , 过点的直线分别交边、的延长线于、 , 连接、 , 若 , 的面积为 , 则四边形的面积为 .23. 如图,在矩形中, , , 动点从点出发以每秒个单位长度的速度沿向终点匀速运动,同时动点从点出发以每秒个单位长度的速度沿折线向终点匀速运动,当点到达终点时,点也随之停止运动以、为邻边构造▱ , 设▱与矩形重叠部分的面积为 , 点的运动时间为秒 . (1)、当时,▱与矩形重叠部分的面积为 ;当时,▱与矩形重叠部分的面积为 ;(2)、当点与点重合时,求的值;(3)、当▱与矩形重叠部分的图形是四边形时,求与之间的函数关系式;(4)、当以、、、为顶点的四边形恰好是平行四边形时,直接写出的值.24. 如图,在平面直角坐标系中,一次函数的图象与轴相交于点 , 与轴相交于点 , 过点作平行于轴的直线 , 交直线于点 , 点是直线上一动点,且点不与点重合,连接、设点的纵坐标为 , 的面积为 .
(1)、当时,▱与矩形重叠部分的面积为 ;当时,▱与矩形重叠部分的面积为 ;(2)、当点与点重合时,求的值;(3)、当▱与矩形重叠部分的图形是四边形时,求与之间的函数关系式;(4)、当以、、、为顶点的四边形恰好是平行四边形时,直接写出的值.24. 如图,在平面直角坐标系中,一次函数的图象与轴相交于点 , 与轴相交于点 , 过点作平行于轴的直线 , 交直线于点 , 点是直线上一动点,且点不与点重合,连接、设点的纵坐标为 , 的面积为 . (1)、点的坐标为 ;(2)、求的值;(3)、求与之间的函数关系式;(4)、当时,以点为直角顶点作等腰直角 , 直接写出点的坐标.
(1)、点的坐标为 ;(2)、求的值;(3)、求与之间的函数关系式;(4)、当时,以点为直角顶点作等腰直角 , 直接写出点的坐标.