云南省重点大学附中2022-2023学年八年级下学期期末数学试卷

试卷更新日期：2023-07-21 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。）

1. 下列等式成立的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $3 \sqrt{3} - 2 \sqrt{3} = 1$ C、 $\pm \sqrt{\frac{1}{3}} = \pm \frac{\sqrt{3}}{3}$ D、 $\sqrt{{(3 - π)}^{2}} = 3 - π$

查看试题解析
2. 如果△ABC的三个顶点A ， B ， C所对的边分别为a ， b ， c ，那么下列条件中，不能判断△ABC是直角三角形的是（）

A、∠A＝25°，∠B＝65° B、∠A：∠B：∠C＝2：3：5 C、a：b：c＝ $\sqrt{2}$ ： $\sqrt{3}$ ： $\sqrt{5}$ D、a＝6，b＝10，c＝12

查看试题解析
3. 下列命题中，假命题是（）

A、四个角都相等的四边形是矩形 B、两组对边分别相等的四边形是平行四边形 C、四条边都相等的四边形是正方形 D、两条对角线互相垂直平分的四边形是菱形

查看试题解析

4. 某中学青年志愿者协会的

10

名志愿者，一周的社区志愿服务时间如表所示：

时间 $/ h$	$2$	$3$	$4$	$5$	$6$
人数	$1$	$3$	$2$	$3$	$1$

关于志愿者服务时间的描述正确的是（）

A、众数是

6

B、中位数是

4

C、平均数是

3

D、方差是

1

查看试题解析

5. 问题情境：“一粒米千滴汗，粒粒粮食汗珠换“ $.$ 为积极响应习近平总书记提出的坚决抵制餐饮浪费行为的重要指示，某送餐公司推出了“半份餐”服务，餐量是整份餐的一半，价格也是整份餐的一半，整份餐单价为 $10$ 元，希望中学每天中午从该送餐公司订 $200$ 份午餐，其中半份餐订 $x$ 份 $(0 < x \leq 200)$ ，其余均为整份餐，该中学每天午餐订单总费用为 $y$ 元则 $y$ 与 $x$ 之间的函数关系式为（）

A、 $y = - 5 x + 2000$ B、 $y = 5 x + 1000$ C、 $y = - 5 x + 1000$ D、 $y = 5 x + 2000$

查看试题解析
6. 如图，平行四边形ABCD中，CE垂直于AB，∠D=53°，则∠BCE的大小是（　　）

A、53° B、43° C、47° D、37°

查看试题解析
7. 如图，在平面直角坐标系中，点 $P$ 坐标为 $(- 3 ， 2)$ ，以点 $O$ 为圆心，以 $O P$ 的长为半径画弧，交 $x$ 轴的负半轴于点 $A$ ，则点 $A$ 的横坐标介于（）

A、 $- 4$ 和 $- 3$ 之间 B、 $- 5$ 和 $- 4$ 之间 C、 $3$ 和 $4$ 之间 D、 $4$ 和 $5$ 之间

查看试题解析

8. 一次函数

y = k x + b

的部分

x

和

y

的部分对应值如表所示，下列结论正确的是（）

$x$	$\dots$	$- 1$	$0$	$1$	$2$	$\dots$
$y$	$\dots$	$5$	$2$	$- 1$	$- 4$	$\dots$

A、

y

随

x

的增大而增大 B、

x = 2

是

k x + b = 0

方程的解 C、此函数图象不经过第三象限 D、此函数图象与

x

轴交于点

(\frac{3}{2} ， 0)

查看试题解析

9. 如图，已知一次函数 $y = k x + 2$ 的图象与 $x$ 轴， $y$ 轴分别交于点 $A$ ， $B$ ，与正比例函数 $y = \frac{1}{3} x$ 交于点 $C$ ，已知点 $C$ 的横坐标为 $2$ ，下列结论： $①$ 关于 $x$ 的方程 $k x + 2 = 0$ 的解为 $x = 3$ ； $②$ 对于直线 $y = k x + 2$ ，当 $x < 3$ 时， $y > 0$ ； $③$ 对于直线 $y = k x + 2$ ，当 $x > 0$ 时， $y > 2$ ； $④$ 方程组 ${\begin{array}{l} 3 y - x = 0 \\ y - k x = 2 \end{array}$ 的解为 ${\begin{array}{l} x = 2 ， \\ y = \frac{2}{3} ． \end{array}$ ，其中正确的是（）

A、 $① ② ③$ B、 $① ② ④$ C、 $① ③ ④$ D、 $② ③ ④$

查看试题解析
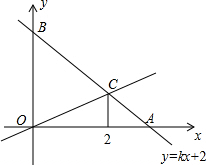10. 如图，在任意四边形 $A B C D$ 中， $M$ ， $N$ ， $P$ ， $Q$ 分别是 $A B$ ， $B C$ ， $C D$ ， $D A$ 的中点，对于四边形 $M N P Q$ 的形状，以下结论中，错误的是（）

A、当 $∠ A B C = 90 °$ 时，四边形 $M N P Q$ 为正方形 B、当 $A C = B D$ 时，四边形 $M N P Q$ 为菱形 C、当 $A C ⊥ B D$ 时，四边形 $M N P Q$ 为矩形 D、四边形 $M N P Q$ 一定为平行四边形

查看试题解析
11. 如图 $1$ ，点 $F$ 从菱形 $A B C D$ 的顶点 $A$ 出发，沿 $A \to D \to B$ 以 $1 c m / s$ 的速度匀速运动到点 $B$ ，图 $2$ 是点 $F$ 运动时， $△ F B C$ 的面积 $y (c m^{2})$ 随时间 $x (s)$ 变化的关系图象，则 $a$ 的值为（）

A、 $\frac{5}{2}$ B、 $2$ C、 $\sqrt{5}$ D、 $2 \sqrt{5}$

查看试题解析
12. 如图，在正方形 $A B C D$ 中， $A B = 2$ ，且 $∠ E A F = 45 ° .$ 则以下结论：
$① A F$ 平分 $∠ E F D$ ； $② B E + D F = E F$ ； $③ △ E C F$ 的周长为 $4$ ； $④ △ A E F$ 的面积等于正方形 $A B C D$ 的面积的一半．其中正确的个数是（）

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析

二、填空题（本大题共4小题，共8.0分）

13. 函数 $y = \frac{1}{\sqrt{2 - x}}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
14. 某中学规定学生体育成绩满分为100分，按课外活动成绩、期中成绩、期末成绩 $2 ： 3 ： 5$ 的比，计算学期成绩.小明同学本学期三项成绩依次为90分、90分、80分，则小明同学本学期的体育成绩是分.

查看试题解析
15. $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 3$ ， $A C = 4$ ， $P$ 为边 $B C$ 上一动点， $P E ⊥ A B$ 于 $E$ ， $P F ⊥ A C$ 于 $F$ ， $M$ 为 $E F$ 中点，则 $A M$ 的最小值为．

查看试题解析
16. 已知 $△ A B C$ 的三个顶点都是同一个正方形的顶点， $∠ A B C$ 的平分线与线段 $A C$ 交于点 $D .$ 若 $△ A B C$ 的一条边长为 $6$ ，则点 $D$ 到直线 $A B$ 的距离为．

查看试题解析

三、解答题（本大题共8小题，共56.0分。）

17. 计算：

(1)、 $2 \sqrt{40} - 5 \sqrt{\frac{1}{10}} - \sqrt{10}$ ；

(2)、 $\sqrt{48} \div \sqrt{3} + 2 \sqrt{\frac{1}{5}} \times \sqrt{30} - (2 \sqrt{2} + \sqrt{3})^{2}$ ．

查看试题解析

18. 某校为了了解初一年级共

480

名同学对环保知识的掌握情况，对他们进行了环保知识测试

.

现随机抽取甲、乙两班各

15

名同学的测试成绩

(

满分

100

分

)

进行整理分析，过程如下：

【收集数据】

甲班 $15$ 名学生测试成绩分别为： $78$ ， $83$ ， $85$ ， $87$ ， $89$ ， $90$ ， $92$ ， $93$ ， $94$ ， $96$ ， $97$ ， $98$ ， $99$ ， $100$ ， $100$

乙班 $15$ 名学生测试成绩中 $90 \leq x < 95$ 的成绩如下： $90$ ， $91$ ， $92$ ， $93$ ， $94$ ．

【整理数据】：

班级	$75 \leq x < 80$	$80 \leq x < 85$	$85 \leq x < 90$	$90 \leq x < 95$	$95 \leq x < 100$
甲	$1$	$1$	$3$	$4$	$6$
乙	$1$	$2$	$3$	$5$	$4$

【分析数据】：

班级	平均数	众数	中位数	方差
甲	$92$	$a$	$93$	$47.3$
乙	$90$	$87$	$b$	$50.2$

【应用数据】：

(1)、根据以上信息，填空：

a =

，

b =

；

(2)、若规定测试成绩

92

分及其以上为优秀，请估计参加环保知识测试的

480

名学生中成绩为优秀的学生共有多少人？

(3)、根据以上数据，你认为哪个班的学生环保知识测试的整体成绩较好？请说明理由

(

一条理由即可

)

．

查看试题解析

19. 拖拉机行驶过程中会对周围产生较大的噪声影响 $.$ 如图 $.$ 有一台拖拉机沿公路 $A B$ 由点 $A$ 向点 $B$ 行驶，已知点 $C$ 为一所学校，且点 $C$ 与直线 $A B$ 上两点 $A$ ， $B$ 的距离分别为 $150 m$ 和 $200 m$ ，又 $A B = 250 m$ ，拖拉机周围 $130 m$ 以内为受噪声影响区域．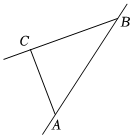

(1)、求 $∠ A C B$ 度数；

(2)、学校 $C$ 会受噪声影响吗？为什么？

(3)、若拖拉机的行驶速度为每分钟 $50$ 米，拖拉机噪声影响该学校持续的时间有多少分钟？

查看试题解析
20. 如图，是一个“函数求值机”的示意图，其中y是x的函数.下面表格中，是通过该“函数求值机”得到的几组x与y的对应值.
输入x
…
$- 6$
$- 4$
$- 2$
0
2
…
输出y
…
$- 6$
$- 2$
2
6
16
…
根据以上信息，解答下列问题：

(1)、当输入的x值为1时，输出的y值为；

(2)、求k，b的值；

(3)、当输出的y值为0时，求输入的x值.

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 交于点 $O$ ， $A E ⊥ B C$ 交 $C B$ 延长线于点 $E$ ， $C F / / A E$ 交 $A D$ 延长线于点 $F$ ．

(1)、求证：四边形 $A E C F$ 是矩形．

(2)、若四边形 $A B C D$ 为菱形， $H$ 为 $A B$ 中点，连接 $O H$ ，若 $D F = 3$ ， $A E = 4$ ，则 $O H$ 长为．

查看试题解析
22. 某小区为了绿化环境，计划分两次购进A，B两种树苗，第一次购进A种树苗30棵，B种树苗15棵，共花费1350元；第二次购进A种树苗24棵，B种树苗10棵，共花费1060元．（两次购进的A，B两种树苗各自的单价均不变）

(1)、A，B两种树苗每棵的价格分别是多少元？

(2)、若购买A，B两种树苗共42棵，总费用为W元，购买A种树苗t棵，B种树苗的数量不超过A种树苗数量的2倍．求W与t的函数关系式．请设计出最省钱的购买方案，并求出此方案的总费用．

查看试题解析
23. 人教版数学八年级下册教材的数学活动 $— —$ 折纸，引起许多同学的兴趣 $.$ 实践发现：对折矩形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展开：以 $B M$ 为折痕再一次折叠纸片，使点 $A$ 落在折痕 $E F$ 上的点 $N$ 处，把纸片展开，连接 $A N$ ．

(1)、求 $∠ M N E$ ；

(2)、如图 $②$ ，折叠矩形纸片 $A B C D$ ，使点 $A$ 落在 $B C$ 边上点 $A'$ 处，并且折痕交 $B C$ 边于点 $T$ ，交 $A D$ 边于点 $S .$ 把纸片展开，连接 $A A'$ 交 $S T$ 于点 $O$ ，连接 $A T .$ 求证：四边形 $S A T A'$ 是菱形．

查看试题解析
24. 如图，矩形 $O A B C$ 的顶点 $A$ 、 $C$ 分别在 $x$ 轴、 $y$ 轴的正半轴上，点 $B$ 的坐标为 $(15 ， 21)$ ，一次函数 $y = - \frac{3}{5} x + 15$ 的图象与边 $O C$ 、 $A B$ 分别交于 $D$ 、 $E$ 两点，点 $M$ 是线段 $D E$ 上的一个动点．

(1)、求证： $O D = B E$ ；

(2)、连结 $O M$ ，若三角形 $O D M$ 的面积为 $37.5$ ，求点 $M$ 的坐标；

(3)、在第 $(2)$ 问的基础上，设点 $P$ 是 $x$ 轴上一动点，点 $Q$ 是平面内的一点，以 $O$ 、 $M$ 、 $P$ 、 $Q$ 为顶点的四边形是菱形，直接写出点 $Q$ 的坐标．

查看试题解析

输入x	…	$- 6$	$- 4$	$- 2$	0	2	…
输出y	…	$- 6$	$- 2$	2	6	16	…