吉林省吉林市船营区2022-2023学年八年级下学期期末考试数学试题

试卷更新日期：2023-07-21 类型：期末考试

进入出卷网下载

一、选择题(每小题2分，共12分)

1. 下列根式中是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
2. 甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是8.9环，方差分别是S_甲²＝0.65，S_乙²＝0.55，S_丙²＝0.50，S_丁²＝0.45，则射箭成绩最不稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 下列四组线段中，可以构成直角三角形的是（　　）

A、2，3，4 B、4，5，6 C、1.5，2.5，3 D、1， $\sqrt{2}$ ， $\sqrt{3}$

查看试题解析
4. 如图，四边形ABCD中，AD＝BC，下列条件不能判定四边形ABCD为平行四边形的是（）

A、AD∥BC B、∠A+∠B＝180° C、∠A＝∠C D、AB＝CD

查看试题解析
5. 如图，直线 y＝-x+2 与 x 轴交于点 A，与 y 轴交于点 B，以点 A 为圆心，AB 长为半径画弧，交 x 轴于点 C，则点 C 的坐标为（）

A、（-1，0） B、（-2 $\sqrt{2}$ ， 0） C、（2 $\sqrt{2}$ -2，0） D、（2-2 $\sqrt{2}$ ， 0）

查看试题解析
6. 如图，在平面直角坐标系中，点A的坐标为（0，3），△OAB沿x轴向右平移后得到△O′A′B′，若点A的对应点A′在直线y＝ $\frac{3}{4}$ x上，则点B与其对应点B′间的距离为（）

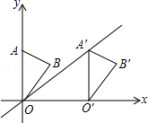A、4 B、3 C、 $\frac{9}{4}$ D、5

查看试题解析

二、填空题 (每小题3分，共24分)

7. 若 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
8. 计算： $\sqrt{{(- 2)}^{2}}$ ＝．

查看试题解析
9. 某灯泡厂为测试一批灯泡的使用寿命，从中随机抽查了50只灯泡，若抽出的50只灯泡的平均使用寿命为 $1680 h$ ，则这批灯泡的平均使用寿命大约是 $h$ ．

查看试题解析
10. 已知直线y=x-3与y=2x+2的交点为（-5，-8），则方程组 ${\begin{cases} x - y - 3 = 0 \\ 2 x - y + 2 = 0 \end{cases}$ 的解是．

查看试题解析
11. 若一次函数y＝-2x+b（b为常数）的图象经过第一，二，四象限，则b的值可以是
.（写出一个即可）

查看试题解析
12. 自由落体的公式是 $h = \frac{1}{2} g t^{2}$ （g为重力加速度， $g = 9.8 {m/s}^{2}$ ），若物体下落的高度h为 $176.4 m$ ，则下落的时间为s．

查看试题解析
13. 如图，△ABC的周长为26cm，中位线EF＝3cm，中位线DF＝6cm，则中位线DE的长为cm.

查看试题解析
14. 将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．如果AB＝ $\sqrt{3}$ ，那么BC的长为．

查看试题解析

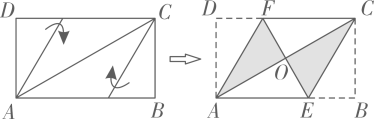
三、解答题(每小题5分，共20分)

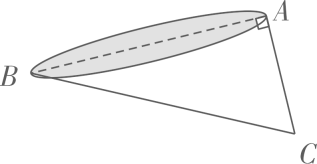
15. 计算：( $\sqrt{24}$ + $\sqrt{0.5}$ )—( $\sqrt{\frac{1}{8}}$ — $\sqrt{6}$ )

查看试题解析
16. 计算： $\sqrt{48}$ ÷（ $\sqrt{\frac{1}{2}}$ × $\sqrt{12}$ ）+ $\sqrt{32}$ .

查看试题解析
17. 若函数y=（2m-1）x+m+3的图象平行于直线y=3x-3 .

(1)、求函数解析式；

(2)、将该函数的图象向下平移3个单位，则平移后的图象与x轴的交点的横坐标为．

查看试题解析
18. 如图，池塘边有两点A，B，点C是与BA方向成直角的AC方向上一点，测得BC=60m，AC=20m，求A，B两点间的距离（结果取整数）.

查看试题解析

四、解答题(每小题7分,共28分)

19. 如图，在□ $A B C D$ 中，以点 $A$ 为圆心，以任意长为半径画圆弧，分别交边AD、AB于点M、N，再分别以点M、N为圆心，以大于 $\frac{1}{2} M N$ 长为半径画圆弧，两弧交于点P，作射线AP交边CD于点E，过点E作EF∥BC交AB于点F．

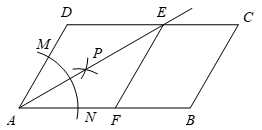(1)、求证：四边形ADEF是菱形；

(2)、若AD＝10，△AED的周长为36，则菱形ADEF的面积是．

查看试题解析
20. 如图，在4×4的网格中每个小正方形边长都是1，每个小格的顶点叫做格点，线段AB的两个端点都在格点上，以格点为顶点分别按下列要求画图．

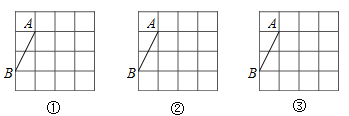(1)、在图①中，以AB为一边画平行四边形ABCD，使其面积为6；

(2)、在图②中，以AB为一边画菱形ABEF；

(3)、在图③中，以AB为一边画正方形ABGH，且与图②中所画的图形不全等．

查看试题解析
21. 如图，在平面直角坐标系中，一次函数y＝kx+b的图象经过点A（-2，4），且与正比例函数y＝- $\frac{2}{3}$ x的图象交于点B（m，2）.

(1)、求一次函数y＝kx+b的解析式；

(2)、若直线AB与x轴交于点C，若连接AO后，则△OAB的面积是．

查看试题解析
22. 每年4月23日是世界读书日，某校为了解学生课外阅读情况，随机抽取20名学生，对每人每周用于课外阅读的平均时间（单位：分钟）进行调查，结果填入下表：
30
60
81
50
40
110
130
146
90
100
60
81
120
140
70
81
10
20
100
81
整理数据：

课外阅读平均时间（x分钟）
0 $\leq$ x $<$ 40
40 $\leq$ x $<$ 80
80 $\leq$ x $<$ 120
120 $\leq$ x $<$ 160
人数
3
5
a
4
分析数据：

平均数
中位数
众数
80
m
n
请根据以上提供的信息，解答下列问题：

(1)、填空：a＝， m＝， n＝；

(2)、已知该校学生1200人，若每人每周用于课外阅读的平均时间不少于80分钟为达标，请估计达标的学生数；

(3)、设阅读一本课外书的平均时间为260分钟，请选择适当的统计量，估计该校学生每人一年（按52周计）平均阅读多少本课外书？

查看试题解析

五、解答题(每小题8分,共16分)

23. 小李、小王分别从甲地出发，骑自行车沿同一条路到乙地参加公益活动．如图，折线OAB和线段CD分别表示小李、小王离甲地的距离y（单位：千米）与时间x（单位：小时）之间的函数关系．根据图中提供的信息，解答下列问题：

(1)、小王的骑车速度是千米/小时，点C的横坐标是；

(2)、求线段AB对应的函数表达式；

(3)、当小王到达乙地时，小李距乙地还有km.

查看试题解析
24. 综合与实践课上，数学老师准备了下面数学活动供同学们探究：
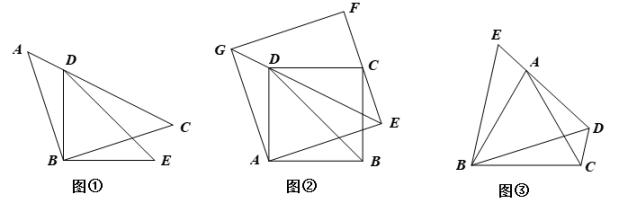
【问题提出】如图①，△ABC和△DBE都是等腰直角三角形，∠ABC＝∠DBE=90°，
点D在AC上．求证：AD²+CD²=DE². 通过连接CE，得AD=CE，∠ACE＝90°. 从而
得出△DCE为直角三角形，使问题得证.

(1)、【问题深入】如图②，四边形ABCD和四边形AEFG都是正方形，点D在对角线EG上．若DG=2，DE=6，求正方形ABCD的面积.

(2)、【问题拓展】如图③，△ABC和△BDE都是等边三角形，点A在DE上，连接DC．则
∠ADC＝ °；若AD=6，AE=2，则△ACD的面积为 .

查看试题解析

六、解答题(每小题10分,共20分)

25. 如图，在四边形ABCD中，AD∥BC，∠B=90°，∠C=60°，AD=24 cm，CD=8 cm．点P从点D出发，以1 cm/s的速度向点A运动；点Q从点B同时出发，以3 cm/s的速度向点C运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点Q的运动时间为x（s）．

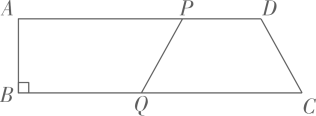(1)、BC=cm，AB=cm；

(2)、当PQ=CD时，求x的值；

(3)、当四边形ABQP为矩形时，x= ．

查看试题解析
26. 因为四边形具有不稳定性，故将边长为1的正方形ABCD压扁为边长为1的菱形ABCD（如图①）．在菱形ABCD中，设∠A=α，面积为S．

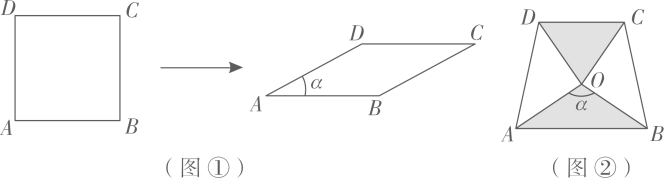(1)、请补全下表：
α
30°
45°
60°
90°
120°
135°
150°
S
          $\frac{1}{2}$
1
          $\frac{\sqrt{3}}{2}$
          $\frac{\sqrt{2}}{2}$

(2)、填空：由（1）可以发现边长是1的正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化．不妨把边长为1，∠A＝α的菱形面积S记为S（α）．
例如：当α＝30°时，S＝S（30°）＝ $\frac{1}{2}$ ，当α＝135°时，S＝S（135°）＝ $\frac{\sqrt{2}}{2}$ .
由上表可以得到S（60°）＝S（°），S（30°）＝S（°），…，由此
可以归纳出S（α）＝S（）.

(3)、将两块相同的等腰直角三角形按图②的方式放置，若AO＝1，∠AOB＝α.
求证：S_△_DOC₌S_△_AOB.

查看试题解析

课外阅读平均时间（x分钟）	0 $\leq$ x $<$ 40	40 $\leq$ x $<$ 80	80 $\leq$ x $<$ 120	120 $\leq$ x $<$ 160
人数	3	5	a	4

α	30°	45°	60°	90°	120°	135°	150°
S	$\frac{1}{2}$			1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$

30	60	81	50	40	110	130	146	90	100
60	81	120	140	70	81	10	20	100	81

平均数	中位数	众数
80	m	n