湖北省黄冈市黄州区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-20 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分.在每小题列出的选项中,选出符合题目的一项)
-
1. 下列根式中,不是最简二次根式的是( )A、 B、 C、 D、2. 匀速地向一个容器注水(注满为止),在注水过程中,若容器中水面高度与注水时间的变化规律如图所示,则这个容器的形状可以是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列说法中,错误的是( )A、平行四边形的对角线互相平分 B、对角线相等的平行四边形是矩形 C、菱形的对角线互相垂直 D、对角线互相垂直的四边形是菱形4. 在平面直角坐标系中,函数的图象经过( )象限.A、第一、第二、第三 B、第二、第三、第四 C、第一、第三、第四 D、第一、第二、第四5. 如图,一棵大树在一次强台风中在距地面处折断,倒下后树顶端着地点距树底端的距离为 , 则这棵大树在折断前的高度为( )
3. 下列说法中,错误的是( )A、平行四边形的对角线互相平分 B、对角线相等的平行四边形是矩形 C、菱形的对角线互相垂直 D、对角线互相垂直的四边形是菱形4. 在平面直角坐标系中,函数的图象经过( )象限.A、第一、第二、第三 B、第二、第三、第四 C、第一、第三、第四 D、第一、第二、第四5. 如图,一棵大树在一次强台风中在距地面处折断,倒下后树顶端着地点距树底端的距离为 , 则这棵大树在折断前的高度为( )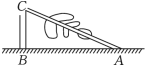 A、 B、 C、 D、6. 矩形中,对角线 , 相交于点 , 如果 , 那么的度数是( )
A、 B、 C、 D、6. 矩形中,对角线 , 相交于点 , 如果 , 那么的度数是( )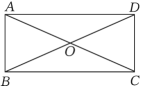 A、 B、 C、 D、7. 如图,在中, , 分别以点和点为圆心,大于的长为半径作弧,两弧相交于、两点,作直线交于点 , 交于点 , 连结 . 若 , , 则的长为( )
A、 B、 C、 D、7. 如图,在中, , 分别以点和点为圆心,大于的长为半径作弧,两弧相交于、两点,作直线交于点 , 交于点 , 连结 . 若 , , 则的长为( )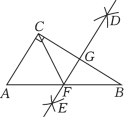 A、 B、2 C、3 D、8. 如图,在中, , , , 点为上任意一点,连结 , 以 , 为邻边作平行四边形 , 连结 , 则的最小值为( )
A、 B、2 C、3 D、8. 如图,在中, , , , 点为上任意一点,连结 , 以 , 为邻边作平行四边形 , 连结 , 则的最小值为( ) A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题(本大题共8小题,每小题3分,共24分)
-
9. 要使二次根式有意义,实数x的取值范围是 .10. 一次函数的图象上有两点 , 则与的大小关系是 .11. 已知一组数据1,2,4,5,的平均数为4,则这组数据的方差为 .12. 如图所示,菱形ABCD的对角线AC,BD相交于点O.若AC=6,BD=8,AE⊥BC,垂足为E,则AE的长为 .
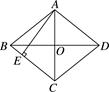 13. 和谐号动车刹车后作匀减速运动,速度与刹车时间与之间满足关系式 . 动车在匀变速直线运动中,从开始刹车到准确停到站台,需要 .14. 若是的小数部分,则 .15. 如图, , , , …,都是等腰直角三角形,其中点 , , …,在轴上,点 , , …,在直线上,若 , 则点的坐标为 .
13. 和谐号动车刹车后作匀减速运动,速度与刹车时间与之间满足关系式 . 动车在匀变速直线运动中,从开始刹车到准确停到站台,需要 .14. 若是的小数部分,则 .15. 如图, , , , …,都是等腰直角三角形,其中点 , , …,在轴上,点 , , …,在直线上,若 , 则点的坐标为 . 16. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人之间的距离(米)与甲出发的时间(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有320米,其中正确的结论有 . (请填写正确结论的序号)
16. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人之间的距离(米)与甲出发的时间(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有320米,其中正确的结论有 . (请填写正确结论的序号)
三、解答题(本大题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 如图,在平行四边形中,过点作于点 , 点在边上,且 , 连接、 .
 (1)、求证:四边形是矩形;(2)、若平分 , , , 求的长.19. 神舟十六号载人飞船已于2023年5月进人太空,3名航天员顺利进驻中国空间站,中国航天员们按预定目标完成各项科考任务,我们期待他们能平安回到祖国大地.星空,探索永无止境,我们都是“追梦人”,为了庆祝我国航天事业的发展,某校举行航空航天作品展,为了解学生上交作品情况,随机调查了部分学生上交作品件数,根据调查结果,绘制了如下两幅不完整的统计图.
(1)、求证:四边形是矩形;(2)、若平分 , , , 求的长.19. 神舟十六号载人飞船已于2023年5月进人太空,3名航天员顺利进驻中国空间站,中国航天员们按预定目标完成各项科考任务,我们期待他们能平安回到祖国大地.星空,探索永无止境,我们都是“追梦人”,为了庆祝我国航天事业的发展,某校举行航空航天作品展,为了解学生上交作品情况,随机调查了部分学生上交作品件数,根据调查结果,绘制了如下两幅不完整的统计图.

图①图②
请根据相关信息,解答下列问题:
(1)、补全两幅统计图;(2)、求所抽取学生上交作品件数的众数与中位数;(3)、求所抽取学生上交作品件数的平均数,若该校共有1200名学生,请估计上交的作品一共有多少件?20. 如图,一次函数的图象分别与x轴和y轴相交于C、两点,且与正比例函数的图象交于点 . (1)、求一次函数的解析式;(2)、当时,直接写出自变量x的取值范围;(3)、点D是一次函数图象上一点,若 , 求点D的坐标.21. 某公司销售型和型两种电脑,其中型电脑每台利润为400元,型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中型电脑的进货量不超过型电脑的2倍,设购进型电脑台,这100台电脑的销售总利润为元.(1)、求关于的函数关系式;(2)、该商店购进型、型电脑各多少台,才能使销售总利润最大,最大利润是多少?22. 某市夏季经常受台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向由点行驶向点 , 已知点为一海港,且点与直线上两点 , 的距离分别为和 , 且 , 以台风中心为圆心周围以内为受影响区域.
(1)、求一次函数的解析式;(2)、当时,直接写出自变量x的取值范围;(3)、点D是一次函数图象上一点,若 , 求点D的坐标.21. 某公司销售型和型两种电脑,其中型电脑每台利润为400元,型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中型电脑的进货量不超过型电脑的2倍,设购进型电脑台,这100台电脑的销售总利润为元.(1)、求关于的函数关系式;(2)、该商店购进型、型电脑各多少台,才能使销售总利润最大,最大利润是多少?22. 某市夏季经常受台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向由点行驶向点 , 已知点为一海港,且点与直线上两点 , 的距离分别为和 , 且 , 以台风中心为圆心周围以内为受影响区域. (1)、求证:;(2)、海港受台风影响吗?为什么?(3)、若台风的速度为 , 则台风影响该海港持续的时间有多长?23.
(1)、求证:;(2)、海港受台风影响吗?为什么?(3)、若台风的速度为 , 则台风影响该海港持续的时间有多长?23. (1)、如图1,在正方形中,是上一点,是延长线上一点,且 , 求证:;(2)、如图2,在正方形中,是上一点,是上一点,如果 , 请你利用(1)的结论证明:;(3)、运用(1)(2)解答中所积累的经验和知识,完成下题:
(1)、如图1,在正方形中,是上一点,是延长线上一点,且 , 求证:;(2)、如图2,在正方形中,是上一点,是上一点,如果 , 请你利用(1)的结论证明:;(3)、运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在直角梯形中, , , , 是上一点,且 , , , 求直角梯形的面积.
24. 如图1,在平面直角坐标系中,直线与轴、轴相交于、两点,点在线段上,将线段绕着点顺时针旋转得到 , 此时点恰好落在直线上,过点作轴于点 . (1)、求证:;(2)、如图2,将沿轴正方向平移得 , 当经过点时,求平移的距离及点的坐标;(3)、在(2)的条件下,若点在轴上,点在直线上,是否存在以、、、为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由.
(1)、求证:;(2)、如图2,将沿轴正方向平移得 , 当经过点时,求平移的距离及点的坐标;(3)、在(2)的条件下,若点在轴上,点在直线上,是否存在以、、、为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由.