湖北省黄冈市四县联合2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-07-20 类型:期末考试
一、选择题(本题共8小题,每小题3分,共24分.在每小题练出的四个选项中,只有是符合题目要求的,不涂、错涂或涂的代号超过一个,一律得0分)
-
1. 下列数中,是无理数的是( )A、0 B、 C、 D、22. 如图,下列条件能判定的是( )
 A、 B、 C、 D、3. 下面调查方式中,合适的是( )A、试航前对我国第一艘国产航母各系统的检查,选择抽样调查方式 B、了解一批袋装食品是否含有防腐剂,选择全面调查方式 C、调查某新型防火材料的防火性稳,采用全面调查的方式 D、为有效维护国家安全,对国外入境人员的身份信息,采用全面调查方式4. 下列式子中,计算正确的是( )A、 B、 C、 D、5. 若 , 则下列结论中,正确的是( )
A、 B、 C、 D、3. 下面调查方式中,合适的是( )A、试航前对我国第一艘国产航母各系统的检查,选择抽样调查方式 B、了解一批袋装食品是否含有防腐剂,选择全面调查方式 C、调查某新型防火材料的防火性稳,采用全面调查的方式 D、为有效维护国家安全,对国外入境人员的身份信息,采用全面调查方式4. 下列式子中,计算正确的是( )A、 B、 C、 D、5. 若 , 则下列结论中,正确的是( )①②③④
A、①②③ B、①③④ C、③④ D、①②③④6. 已知点 , 将它先向左平移5个单位,再向上平移4个单位后得到点Q,则点Q的坐标是( )A、 B、 C、 D、7. 《孙子算经》中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸:屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长水,长木还剩余1尺,问木长多少尺。设木长为x尺,绳子长为y尺,则下列符合题意的方程组是( )A、 B、 C、 D、8. 关于x的不等式组恰好只有两个整数解,则a的取值范围为( )A、 B、 C、 D、二、填空题(本大题共8小题,每小题3分,共24分.请将结果直接写在答题卡上相应位置上)
-
9. 如图,已知直线AB、CD相交于点O. , . 则度.
 10. 计算: ,11. 体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:cm)的最大值为175,最小值为155.若取组距为3,则可以分成组.12. 如图,OC是的平分线,直线 . 若 , 则的大小为 .
10. 计算: ,11. 体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:cm)的最大值为175,最小值为155.若取组距为3,则可以分成组.12. 如图,OC是的平分线,直线 . 若 , 则的大小为 . 13. 已知: , 若是整数,则 .14. 已知 是关于x,y的二元一次方程组 的一组解,则a+b= .
13. 已知: , 若是整数,则 .14. 已知 是关于x,y的二元一次方程组 的一组解,则a+b= .
15. 如图,直线m与的一边射线OB相交, , 向上平移直线m得到直线n.与的另一边射线OA相交,则 . 16. 小明到某服装商场进行社会调查,了解到该商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服装1件共算350元;如果购买甲服装1件,乙服装2件,丙服装3件共需370元。某顾客想购买甲、乙、丙服装各一件共需元,
16. 小明到某服装商场进行社会调查,了解到该商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服装1件共算350元;如果购买甲服装1件,乙服装2件,丙服装3件共需370元。某顾客想购买甲、乙、丙服装各一件共需元,三、解答题(本大题共8小题,满分72分.解答写在答题卡上)
-
17.(1)、解方程组(2)、解不等式组并把解集在数轴上表示出来。
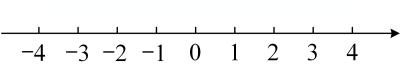 18. 已知的立方根是3,的算术平方根是3,c是的整数部分,求的平方根。19. 与在平面直角坐标系中的位置如图所示.
18. 已知的立方根是3,的算术平方根是3,c是的整数部分,求的平方根。19. 与在平面直角坐标系中的位置如图所示. (1)、分别写出下列各点的坐标:A;B;C;(2)、由经过怎样的平移得到?答: .(3)、若点是内部一点,则内部的对应点的坐标为;(4)、求的面积,20. 为减少传统塑料袋对生态环境的破坏,国家提倡使用可以在自然环境下(特定微生物、温度、温度)较快完成降解的环保塑料袋。调查小组就某小区每户家庭1周内环深塑料袋的使用情况进行了抽样调查,使用情况为A(不使用)、B(1~3个)、C(4~6个)、D(7个及以上),以下是根据调查结果绘制的统计图的一部分.
(1)、分别写出下列各点的坐标:A;B;C;(2)、由经过怎样的平移得到?答: .(3)、若点是内部一点,则内部的对应点的坐标为;(4)、求的面积,20. 为减少传统塑料袋对生态环境的破坏,国家提倡使用可以在自然环境下(特定微生物、温度、温度)较快完成降解的环保塑料袋。调查小组就某小区每户家庭1周内环深塑料袋的使用情况进行了抽样调查,使用情况为A(不使用)、B(1~3个)、C(4~6个)、D(7个及以上),以下是根据调查结果绘制的统计图的一部分. (1)、本次调查的样本容量是 ▲ , 请补全条形统计图:(2)、已知该小区有1500户家庭,调查小组估计:该小区1周内使用7个及以上环保塑料袋的家庭约有225户,调查小组的估计是否合理?请说明理由.21. 如图, , .
(1)、本次调查的样本容量是 ▲ , 请补全条形统计图:(2)、已知该小区有1500户家庭,调查小组估计:该小区1周内使用7个及以上环保塑料袋的家庭约有225户,调查小组的估计是否合理?请说明理由.21. 如图, , . (1)、试说明:;(2)、若DG是的平分线, , 求的度数。22. 多功能家庭早餐机可以制作多种口味的美食,深受消费者的喜爱,在新品上市促销活动中,已知8台A型早餐机和3台B型早餐机需要1000元,6台A型早餐机和1台B型早餐机需要600元.(1)、每台A型早餐机和每台B型早餐机的价格分别是多少元?(2)、某商家欲购进A,B两种型号早餐机共20台,但总费用不超过2200元,那么至少要购进A型早餐机多少台?23. 同学们学习了有理数乘法,不等式组与方程组的知识,它们之间有着一定的逻辑关联,请解决以下问题:(1)、阅读理解:解不等式 .
(1)、试说明:;(2)、若DG是的平分线, , 求的度数。22. 多功能家庭早餐机可以制作多种口味的美食,深受消费者的喜爱,在新品上市促销活动中,已知8台A型早餐机和3台B型早餐机需要1000元,6台A型早餐机和1台B型早餐机需要600元.(1)、每台A型早餐机和每台B型早餐机的价格分别是多少元?(2)、某商家欲购进A,B两种型号早餐机共20台,但总费用不超过2200元,那么至少要购进A型早餐机多少台?23. 同学们学习了有理数乘法,不等式组与方程组的知识,它们之间有着一定的逻辑关联,请解决以下问题:(1)、阅读理解:解不等式 .解:根据两数相乘,同号得正,原不等式可以转化为或 ,
解不等式组 , 得;解不等式组 , 得
∴原不等式的解集为或 .
问题解决:根据以上材料,解不等式 .
(2)、已知关于x,y的方程组的解满足不等式组 , 求满足条件的m的整数值。24. 如图1,点A的坐标为 , 将点A向右平移b个单位得到点B,其中关于x的一元一次不等式的解集为 , 过点B作轴于C. (1)、求B点坐标及;(2)、如图2,点Q自O点以1个单位/秒的速度在y轴上向上运动,点P自C点以2个单位/秒的速度在x轴上向左适动.设运动的时间为t秒().是否存在一段时间,使得?若存在,求t的取值范围;若不存在,说明理由;(3)、在(2)的条件下,求 .
(1)、求B点坐标及;(2)、如图2,点Q自O点以1个单位/秒的速度在y轴上向上运动,点P自C点以2个单位/秒的速度在x轴上向左适动.设运动的时间为t秒().是否存在一段时间,使得?若存在,求t的取值范围;若不存在,说明理由;(3)、在(2)的条件下,求 .