湖北省黄石市大冶市2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-20 类型:期末考试
一、选择题(本大题共10小题,共30分.在每小题列出的选项中,选出符合题目的一项).
-
1. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、2. 代数式有意义时,应满足的条件为( )A、 B、 C、 D、3. 下列等式成立的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数均是9.2环,方差分别是 , , , , 则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 如图,是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是2,直角三角形较长的直角边为m,较短的直角边为n,那么的值为( )
 A、23 B、24 C、25 D、266. 如图,在平行四边形中,以为圆心,长为半径画弧交于点.分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 若 , , 则的长为( )
A、23 B、24 C、25 D、266. 如图,在平行四边形中,以为圆心,长为半径画弧交于点.分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 若 , , 则的长为( ) A、4 B、6 C、8 D、107. 已知一次函数 , , 且y随x的增大而增大,则此图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 下列判断错误的是( )A、两组对边分别平行的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、邻边相等的平行四边形是菱形 D、两条对角线垂直且平分的四边形是正方形9. 小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离与小王的行驶时间之间的函数关系,下列结论错误的是( )
A、4 B、6 C、8 D、107. 已知一次函数 , , 且y随x的增大而增大,则此图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 下列判断错误的是( )A、两组对边分别平行的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、邻边相等的平行四边形是菱形 D、两条对角线垂直且平分的四边形是正方形9. 小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离与小王的行驶时间之间的函数关系,下列结论错误的是( ) A、走完全程,小李所用的时间是小王的 B、小李骑车的速度为 C、的值为15 D、小王骑车的速度为10. 我国著名数学家华罗庚曾说:“数缺形时少直观,形缺数时难入微”.请用这句话提到的数学思想方法解决下面的问题,已知函数 , 且关于 , 的二元一次方程有两组解,则的取值范围是( )A、 B、 C、 D、
A、走完全程,小李所用的时间是小王的 B、小李骑车的速度为 C、的值为15 D、小王骑车的速度为10. 我国著名数学家华罗庚曾说:“数缺形时少直观,形缺数时难入微”.请用这句话提到的数学思想方法解决下面的问题,已知函数 , 且关于 , 的二元一次方程有两组解,则的取值范围是( )A、 B、 C、 D、二、填空题(本大题共8小题,11- -17每小题3分,18小题4分,共25分)
-
11. 已知 , 则的值为 .12. 实数 , 在数轴上的位置如图所示,则化简的结果是 .
 13. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .14. 如图,四边形是平行四边形,若 , 则 .
13. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .14. 如图,四边形是平行四边形,若 , 则 . 15. 若三角形的三边长分别等于 , ,2,则此三角形的面积为 .
15. 若三角形的三边长分别等于 , ,2,则此三角形的面积为 .
16. 将直线的图象向右平移3个单位长度后所得直线的解析式是 .17. 如图,点是的角平分线上的一点,过点作交于点C, , 若 , , 则 .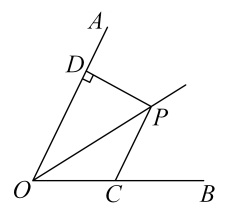 18. 如图,矩形中, , , 为边上一动点,以为边构造等边(点位于下方),连接 , 则
18. 如图,矩形中, , , 为边上一动点,以为边构造等边(点位于下方),连接 , 则
①当时,;
②点在运动的过程中,的最小值为 .
三、解答题(本大题共8小题,共65分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算:20. 在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
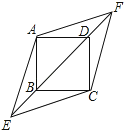 (1)、求证:△ABE≌△ADF;(2)、试判断四边形AECF的形状,并说明理由.21. 如图,在平面直角坐标系内,直线AB与x轴交于点 , 与y轴交于点.
(1)、求证:△ABE≌△ADF;(2)、试判断四边形AECF的形状,并说明理由.21. 如图,在平面直角坐标系内,直线AB与x轴交于点 , 与y轴交于点.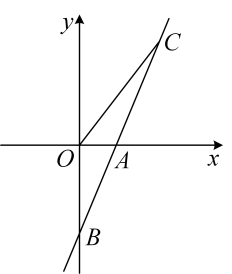 (1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且 , 求点的坐标.22. 请阅读下列材料:
(1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且 , 求点的坐标.22. 请阅读下列材料:问题:已知 , 求代数式的值.小敏的做法是:根据得 , , 得:.把作为整体代入:得.即:把已知条件适当变形,再整体代入解决问题.请你用上述方法解决下面问题:
(1)、已知 , 求代数式的值;(2)、已知 , 求代数式的值.23. 为了了解某校学生的身高状况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同、根据所得数据绘制如图所示的统计图表.

组织
身高(cm)
A
B
C
D
E
已知女生身高在A组的有8人,根据图表中提供的信息,回答下列问题:
(1)、补充图中的男生身高情况直方图,男生身高的中位数落在组(填组别字母序号);(2)、在样本中,身高在之间的人数共有 . 人,身高人数最多的在组(填组别序号);(3)、已知该校共有男生400人,女生420人,请估计身高不足160的学生约有多少人?24. 某商场准备购进甲乙两种服装进行销售.甲种服装每件进价160元,售价220元;乙种服装每件进价120元,售价160元.现计划购进两种服装共100件,其中甲种服装不少于60件.设购进甲种服装x件,两种服装全部售完,商场获利y元(1)、求y与x之间的函数关系式;(2)、若购进100件服装的总费用不超过15000元,求最大利润为多少元?(3)、在(2)的条件下,该服装店对甲种服装以每件优惠()元的价格进行优惠促销活动,乙种服装每件进价减少b元,售价不变,且 , 若最大利润为4950元,请直接写出a的值.


