湖北省孝感市孝南区2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-07-20 类型：期末考试

进入出卷网下载

一、精心选一选（本大题共8小题，每小题3分，共24分，每小题只有一个选项是正确的）

1. 9的算术平方根是（）

A、3 B、 $\pm 3$ C、 $\pm \sqrt{3}$ D、 $\sqrt[3]{9}$

查看试题解析
2. 下列调查方式最适合的是（）

A、了解某超市火腿肠的质量，采用普查方式 B、了解某班同学的视力情况，采用抽样调查方式 C、了解某市居民节约用水意识情况，采用普查方式 D、了解长江流域鱼的数量，采用抽样调查方式

查看试题解析
3. 下列各选项中能用“垂线段最短”来解释的现象是（）

A、 B、 C、 D、

查看试题解析
4. 方程组 ${\begin{array}{l} 2 x + y = □ \\ x + y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = □ \end{array}$ ，则被 $□$ 遮盖的两个数分别为（）

A、2，1 B、2，3 C、5，1 D、2，4

查看试题解析
5. 如图，下列条件中不能判断 $a ∥ b$ 的是（）

A、 $∠ 2 = ∠ 6$ B、 $∠ 3 = ∠ 6$ C、 $∠ 5 = ∠ 6$ D、 $∠ 4 + ∠ 6 = 180 °$

查看试题解析
6. 若 $a > b$ 则下列式子中正确的是（）

A、 $\frac{a}{2} < \frac{b}{2}$ B、 $a - 3 < b - 3$ C、 $- 3 a < - 3 b$ D、 $b - a > 0$

查看试题解析
7. 《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之：余绳四尺五寸；屈绳量之，不足一尺.木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问木长多少尺？设木长为 $x$ 尺，绳子长为 $y$ 尺，则下列符合题意的方程组是（）

A、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ B、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ C、 ${\begin{array}{l} y = 4.5 - x \\ \frac{1}{2} y = x + 1 \end{array}$ D、 ${\begin{array}{l} y = 4.5 - x \\ \frac{1}{2} y = x - 1 \end{array}$

查看试题解析
8. 如图， $A B ∥ C D$ ， ∠M＝44°，AN平分∠BAM，CN平分∠DCM，则∠N等于（）

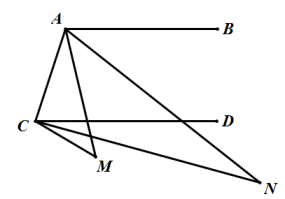A、21.5° B、21° C、22.5° D、22°

查看试题解析

二、细心填一填（本大题共8小题，每小题3分，共24分）

9. 已知点 $A$ 在第四象限，到 $x$ 轴的距离是5，到 $y$ 轴的距离是6，点 $A$ 的坐标为.

查看试题解析
10. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 4 \\ b x + a y = 5 \end{array}$ 的解，则 $a + b =$ .

查看试题解析
11. 已知 $P$ 点坐标为 $(2 + m ， 3 m - 3)$ ，且点 $P$ 在 $y$ 轴上，则点 $P$ 的坐标是.

查看试题解析
12. 学校为了解本校初三年级学生上学的交通方式，随机抽取了本校20名初三学生进行调查，其中有2名学生是乘私家车上学，上图是收集数据后绘制的扇形图，如果该校初三年级有200名学生，那么骑自行车上学的学生大约有人.

查看试题解析
13. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} 4 x + 10 > k \\ 1 - x ⩾ 0 \end{array}$ 有且只有四个整数解，则符合条件的所有整数 $k$ 的和为.

查看试题解析
14. 如图，直线a，b被直线c所截，若a∥b，∠1=110°，∠2=40°，则∠3=°.

查看试题解析
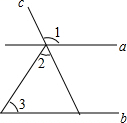15. 某正数的两个平方根分别是 $a + 3$ 、 $2 a - 15$ ，则这个正数为.

查看试题解析
16. 数学符号是数学语言中区别于本土语言的特有字符，它表示一定的含义.设数学符号 $(x]$ 表示大于 $x$ 的最小整数，如 $(2] = 3$ ， $(- 1.4] = - 1$ ，则下列结论：
① $(0] = 1$ ；②当 $x$ 是有理数时， $(x] > x$ 成立；③ $(x] - x$ 可能为负值；④若 $x$ 满足不等式组 ${\begin{array}{l} \frac{x + 2}{2} < 1 \\ 2 - 3 x \leq 5 \end{array}$ ，则 $(x]$ 的值为0.
其中正确结论的序号为.

查看试题解析

三、用心做一做（本大题共8小题，共72分）

17. 计算。

(1)、 $- 3^{2} + \sqrt{16} + | - 1 | + \sqrt[3]{27}$

(2)、解方程组 ${\begin{array}{l} 2 x + 3 y = 11 \\ x - 3 y = 1 \end{array}$

查看试题解析
18. 解不等式组： ${\begin{array}{l} x - 3 (x - 2) ⩾ 4 \\ \frac{x - 1}{5} < \frac{x + 1}{2} \end{array}$ ，并写出它的整数解.

查看试题解析
19. 4月22日是“世界地球日”，某校为调查学生对相关知识的了解情况，从全校学生中随机抽取 $n$ 名学生进行测试，测试成绩进行整理后分成五组，并绘制成如下的频数分布直方图和扇形统计图。

(1)、 $m =$ ， $n =$ ，补全频数分布直方图；

(2)、在泬形统计图中，“70~80”这组的扇形圆心角为°；

(3)、若成缜达到80分以上为优秀，请你估计全校1200名学生对“世界地球日”相关知识了解情况为优秀的学生人数.

查看试题解析
20. 如图， $D$ 、 $E$ 、 $F$ 分别在 $△ A B C$ 的三条边上， $D E ∥ A B$ ， $∠ 1 + ∠ 2 = 180 °$ .

(1)、试说明： $D F ∥ A C$

(2)、若 $∠ 1 = 100 °$ ， $D F$ 平分 $∠ B D E$ ，求 $∠ C$ 的度数.

查看试题解析
21. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (- 2 ， 1)$ ， $B (- 3 ， - 2)$ ， $C (1 ， - 2)$ ，将 $△ A B C$ 先向上平移3个单位长度，再向右平移2个单位长度后，得到 $△ A_{1} B_{1} C_{1}$ .

(1)、在图中画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、连接 $A A_{1}$ ， $C C_{1}$ ，则这两条线段的长度关系是；

(3)、若点 $P$ 在 $x$ 轴上运动，当线段 $P A$ 长度最小时，点 $P$ 的坐标为；

(4)、在平移的过程中，线段 $A C$ 扫过的图形的面积为

查看试题解析
22. 某电器超市销售每台进价分别为160元、120元的 $A$ 、 $B$ 两种型号的电风扇，下表是近两周的销售情况：
销售时段
销售数量
销售收入
          $A$ 种型号
          $B$ 种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
（进价、售价均保持不变，利润 $=$ 销售收入－进货成本）

(1)、求 $A$ 、 $B$ 两种型号的电风扇的销售单价；

(2)、超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，
①求 $A$ 种型号的电风扇最多能采购多少台？
②若超市销售完这50台电风扇能实现利润超过1850元的目标，有几种采购方案？

查看试题解析
23.
[课题学习]：
平行线的“等角转化”功能.

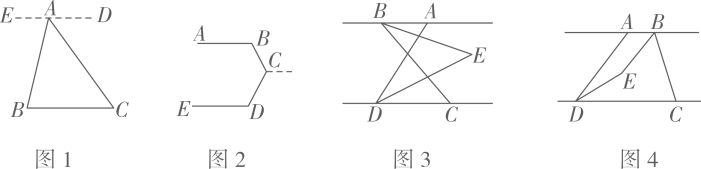(1)、[阅读理解]：
如图1，已知点 $A$ 是 $B C$ 外一点，连接 $A B$ ， $A C$ ，求 $∠ B A C + ∠ B + ∠ C$ 的度数.
阅读并补充下面推理过程.
解：过点 $A$ 作 $E D ∥ B C$ ，所以 $∠ B =$ ， $∠ C =$
又因为 $∠ E A B + ∠ B A C + ∠ D A C = 180 °$
所以 $∠ B + ∠ B A C + ∠ C = 180 °$

(2)、[方法运用]：
如图2，已知 $A B ∥ E D$ ，求 $∠ B + ∠ B C D + ∠ D$ 的度数.

(3)、[深化拓展]：
已知 $A B ∥ C D$ ，点 $C$ 在 $D$ 的右侧， $∠ A D C = 70 °$ ， $B E$ 平分 $∠ A B C$ ， $D E$ 平分 $∠ A D C$ ， $B E$ ， $D E$ 所在的直线交于点 $E$ ，点 $E$ 在 $A B$ 与 $C D$ 两条平行线之间.
①如图3，若 $∠ A B C = 60 °$ ，则 $∠ B E D =$ °
②如图4，点 $B$ 在点 $A$ 的右侧，若 $∠ A B C = n °$ ，则 $∠ B E D =$ °（用含 $n$ 的代数式表示）

查看试题解析
24. 如图，在平面直角坐标系中， $O$ 为坐标原点，点 $A (a ， b)$ 、 $B (c ， 0)$ ，其中 $a$ ， $b$ ， $c$ 满足 $| a - 2 | + {(b - 3)}^{2} + \sqrt{c + 4} = 0$ ， $D$ 为直线 $A B$ 与 $y$ 轴的交点， $C$ 为线段 $A B$ 上一点，其纵坐标为 $t$ .

(1)、求 $a$ ， $b$ ， $c$ 的值；

(2)、当 $t$ 为何值时， $△ B O C$ 和 $△ A O D$ 面积的相等；

(3)、若点 $C$ 坐标为 $(- 2 ， 1)$ ，点 $M (m ， - 3)$ 在第三象限内，满足 $S_{△ M O C} ⩾ 5$ ，求 $m$ 的取值范围.（注： $S_{△ M O C}$ 表示 $△ M O C$ 的面积）

查看试题解析

销售时段	销售数量		销售收入
销售时段	$A$ 种型号	$B$ 种型号	销售收入
第一周	3台	4台	1200元
第二周	5台	6台	1900元