湖北省随州市随县2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-07-20 类型：期末考试

进入出卷网下载

一、选择题（本题共10个小题，每小题3分，共30分，每小题给出的四个选项中，只有一个是正确的）

1. 在实数 $\frac{22}{7}$ ， $- \sqrt{5}$ ， $\frac{π}{2}$ ， $\sqrt[3]{8}$ ， 3.14，0.010010001中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 如图，把等腰直角三角板的直角顶点放在刻度尺的一边上，若∠1＝60°，则∠2的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
3. 若点 $P (3 - m ， m - 1)$ 在第二象限，则 $m$ 的取值范围是（）

A、 $m > 3$ B、 $m < 1$ C、 $m > 1$ D、 $1 < m < 3$

查看试题解析
4.
如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（　　）

A、两直线平行，同位角相等 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、同位角相等，两直线平行

查看试题解析
5. 下列各组数中，互为相反数的是（）

A、 $- \sqrt{9}$ 与 $\sqrt[3]{27}$ B、 $\sqrt[3]{- 8}$ 与 $- \sqrt[3]{8}$ C、 $| - \sqrt{2} |$ 与 $\sqrt{2}$ D、 $\sqrt{2}$ 与 $\sqrt[3]{- 8}$

查看试题解析
6. 如图所示，以下四个结论中正确的是（）

A、（2）班学生最少 B、（3）班男生人数是女生人数的2倍 C、（4）班女生比男生多 D、（2）班和（4）班学生一样多

查看试题解析
7. 下列命题：①经过直线外一点，有且只有一条直线与这条直线平行；②在同一平面内，过一点有且只有一条直线与已知直线垂直；③互为邻补角的两角的角平分线互相垂直；④如果直线 $a / / b$ ， $b ⊥ c$ ，那么 $a / / c$ ．其中是真命题的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图， $A B / / C D$ ， $∠ A E F = 52 °$ ， $F G$ 平分 $∠ E F D$ ，则 $∠ B G F$ 的度数等于（）

A、 $154 °$ B、 $152 °$ C、 $136 °$ D、 $144 °$

查看试题解析
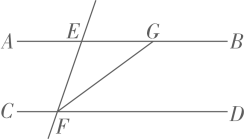9. 我国古代数学著作《九章算术》记载了一道“牛马问题”：“今有二马、一牛价过一万，如半马之价．一马、二牛价不满一万，如半牛之价．问牛、马价各几何．”其大意为：现有两匹马加一头牛价钱超过一万，超过的部分正好是半匹马的价钱；一匹马加上二头牛的价钱则不到一万，不足部分正好是半头牛的价钱，求一匹马、一头牛各多少钱？设一匹马价钱为 $x$ 元，一头牛价钱为 $y$ 元，则符合题意的方程组是（）

A、 ${\begin{array}{l} 2 x + y - 10000 = \frac{x}{2} \\ 10000 - (x + 2 y) = \frac{y}{2} \end{array}$ B、 ${\begin{array}{l} 2 x + y - 10000 = \frac{x}{2} \\ x + 2 y - 10000 = \frac{y}{2} \end{array}$ C、 ${\begin{array}{l} 2 x + y + 10000 = \frac{x}{2} \\ x + 2 y - 10000 = \frac{y}{2} \end{array}$ D、 ${\begin{array}{l} 2 x + y + 10000 = \frac{x}{2} \\ 10000 - (x + 2 y) = \frac{y}{2} \end{array}$

查看试题解析
10. 如图，在平面直角坐标系中，半径均为1个单位长度的半圆组成一条平滑的曲线，点 $P$ 从原点 $O$ 出发，沿这条曲线向右运动，速度为每秒 $\frac{π}{2}$ 个单位长度，则第2023秒时，点 $P$ 的坐标是（）

A、 $(2023 ， 1)$ B、 $(2023 ， - 1)$ C、 $(2022 ， - 1)$ D、 $(2023 ， 0)$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. $| \sqrt{2} - \sqrt{3} | + 2 \sqrt{2}$ 的值是．

查看试题解析
12. 用“>”或“<”填空：若 $- 2 a + 1 < - 2 b + 1$ ，则ab.

查看试题解析
13. 如图，点E是长方形纸片ABCD的边AB上一点，沿CE折叠纸片交DC于点F，且 $∠ E F D = 76 °$ ，则 $∠ E C F$ 的度数是．

查看试题解析
14. 小明将本班全体同学某次数学测试成绩制成了频数分布直方图，图中从左到右各小长方形的高之比为 $4 ： 3 ： 7 ： 6$ ，且第一小组的频数是8，则小明班的学生人数是人．

查看试题解析
15. 若方程组 ${\begin{array}{l} 3 x + y = a + 1 \\ x + 3 y = 3 \end{array}$ 的解x，y满足 $x + y > 5$ ，则 $a$ 的取值范围为．

查看试题解析
16. 如图，长方形 $O A B C$ 在平面直角坐标系中，其中 $A (4 ， 0)$ ， $C (0 ， 3)$ ，点 $E$ 是 $B C$ 的中点，动点 $P$ 从 $O$ 点出发，以每秒 $1 c m$ 的速度沿 $O - A - B -$ $E$ 运动，最终到达点 $E$ ．若点 $P$ 运动的时间为 $x$ 秒，那么当 $x = 2$ 秒时， $△ O P E$ 的面积等于 $c m^{2}$ ；当 $△ O P E$ 的面积等于 $5 c m^{2}$ 时， $P$ 点坐标为．

查看试题解析

三、解答题（本大题共8小题，共72分）

17.

(1)、解二元一次方程组： ${\begin{array}{l} x - 5 y = 0 \\ 3 x + 2 y = 17 \end{array}$ ；

(2)、解不等式组： ${\begin{array}{l} 2 (x - 2) \leq 3 - x \\ 1 - \frac{2 x + 1}{3} > x + 1 \end{array}$

查看试题解析
18. 在正方形网格中，每个小正方形的边长均为1个单位长度， $△ A B C$ 的三个顶点A，B，C都在格点（正方形网格的交点称为格点）上．现将 $△ A B C$ 平移，使点A平移到点D，点E，F分别是B，C的对应点．

⑴在图中请画出平移后的 $△ D E F$ ，并求出 $△ D E F$ 的面积是 ▲ ；

⑵在网格中标出所有满足条件的格点P（A点除外），使 $S_{△ A B C} = S_{△ B C P}$ ．

查看试题解析
19. 完成下面的证明．
已知：如图， $B C / / D E$ ， $B E$ ， $D F$ 分别是 $∠ A B C$ ， $∠ A D E$ 的平分线．

求证： $∠ 1 = ∠ 2$ ．

证明： $∵ B C / / D E$ ，

      $∴ ∠ A B C = ∠ A D E$ （）．

      $∵ B E$ ， $D F$ 分别是 $∠ A B C$ ， $∠ A D E$ 的平分线．

      $∴ ∠ 3 = \frac{1}{2} ∠ A B C$ ， $∠ 4 = \frac{1}{2} ∠ A D E$ ．

      $∴ ∠ 3 = ∠ 4$ ．

      $∴$       ▲       $/ /$       ▲       ．（）

      $∴ ∠ 1 = ∠ 2$ ．（）

查看试题解析
20. 如图，直线 $E F / / M N$ ，点 $B$ 在直线MN上，且 $A B ⊥ B C$ ， $∠ 1 = 55 °$ ，求 $∠ 2$ 的度数．

查看试题解析
21. 为了创设全新的校园文化氛围，进一步组织学生开展课外阅读，让学生在丰富多彩的书海中，扩大知识源，亲近母语，提高文学素养．某校准备开展“与经典为友、与名著为伴”的阅读活动，活动前对本校学生进行了“你最喜欢的图书类型（只写一项）”的随机抽样调查，相关数据统计如下：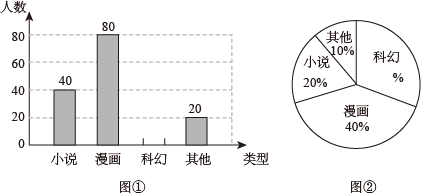
请根据以上信息解答下列问题：

(1)、该校对多少名学生进行了抽样调查？

(2)、请将图①和图②补充完整；

(3)、已知该校共有学生800人，利用样本数据估计全校学生中最喜欢小说的人数约为多少人？

查看试题解析
22. 某学校要成立无人机兴趣小组，需要购买A型和B型两种无人机配件．据了解，购买1个A型配件和3个B型配件需要支付530元；购买3个A型配件和2个B型配件需要支付890元．

(1)、求购买1个A型配件和1个B型配件各需要支付多少元？

(2)、该学校决定购买A型配件和B型配件共30个，总费用不超过4180元，则最多可以购买多少个A型配件？

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，给出如下定义：点 $A$ 到 $x$ 轴， $y$ 轴距离的较小值称为点 $A$ 的“短距”，当点P的“短距”等于点Q的“短距”时，称P，Q两点为“等距点”．

(1)、点 $A (- 5 ， - 2)$ 的“短距”为；

(2)、点 $B (- 2 ， - 2 m + 1)$ 的“短距”为1，求 $m$ 的值；

(3)、若 $C (- 1 ， k + 3)$ ， $D (4 ， 2 k - 3)$ 两点为“等距点”，求 $k$ 的值．

查看试题解析
24. 已知 $A M / / C N$ ，点 $B$ 为平面内一点， $A B ⊥ B C$ 于 $B$ ．

(1)、如图1，直接写出 $∠ A$ 和 $∠ C$ 之间的数量关系；

(2)、如图2，过点 $B$ 作 $B D ⊥ A M$ 于点 $D$ ，求证： $∠ A B D = ∠ C$ ；

(3)、如图3，在（2）问的条件下，点E，F在DM上，连接BE，BF，CF，BF平分 $∠ D B C$ ， $B E$ 平分 $∠ A B D$ ，若 $∠ F C B + ∠ N C F = 180 °$ ， $∠ B F C = 3 ∠ D B E$ ，直接写出 $∠ E B C$ 的度数．

查看试题解析