福建省泉州市德化县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-07-20 类型:期末考试
一、选择通:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
-
1. 方程2x=6的解是( )A、 B、 C、 D、2. 下列三条线段能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 如图,数轴上表示的不等式的解集为( )
 A、 B、 C、 D、4. 下列式子变形正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得5. 如图,已知 , 点 , , , 在同一条直线上,若 , , 则线段的长为( )
A、 B、 C、 D、4. 下列式子变形正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得5. 如图,已知 , 点 , , , 在同一条直线上,若 , , 则线段的长为( )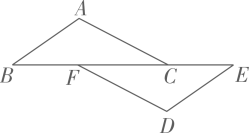 A、2 B、2.5 C、3 D、56. 只用下列四种规格相同的正多边形中的一种不能铺满地面的是( )A、正六边形 B、正五边形 C、正方形 D、正三角形7. 我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?”其大意是:几个人一起去购买某物品,若每人出8钱,则多了3钱;若每人出7钱,则少了4钱.问有多少人,物品的价格是多少钱?设共有人,物品价格为钱,则根据题意可列方程组为( )A、 B、 C、 D、8. 将一个正八边形与一个正六边形如图放置,顶点 , , , 四点在同一条直线上,为公共顶点则等于( )
A、2 B、2.5 C、3 D、56. 只用下列四种规格相同的正多边形中的一种不能铺满地面的是( )A、正六边形 B、正五边形 C、正方形 D、正三角形7. 我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?”其大意是:几个人一起去购买某物品,若每人出8钱,则多了3钱;若每人出7钱,则少了4钱.问有多少人,物品的价格是多少钱?设共有人,物品价格为钱,则根据题意可列方程组为( )A、 B、 C、 D、8. 将一个正八边形与一个正六边形如图放置,顶点 , , , 四点在同一条直线上,为公共顶点则等于( )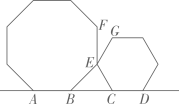 A、80° B、75° C、65° D、55°9. 如图,是由绕点顺时针旋转得到的.若点恰好在的延长线上,且 , 则等于( )
A、80° B、75° C、65° D、55°9. 如图,是由绕点顺时针旋转得到的.若点恰好在的延长线上,且 , 则等于( )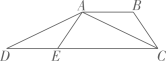 A、120° B、125° C、130° D、135°10. 已知 , 为任意有理数.
A、120° B、125° C、130° D、135°10. 已知 , 为任意有理数.①关于的方程的解为
②关于的方程可能是一元一次方程
③当时,关于的方程的解是
④当时,关于的方程的解是
以上说法正确的是( )
A、①③ B、②③ C、②④ D、③④二、填空题:本题共6小题,每小题4分,共24分.
-
11. 在中,当时,的值是 .12. 若是方程的一个解,则 .13. 代数式与的和大于9,则的取值范围是 .14. 如图,点 , 分别在的边 , 上,现将沿着折叠,已知 , , 则 .
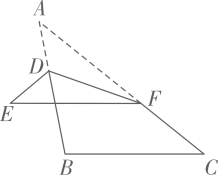 15. 在中,为锐角,为的高,且 , 则的大小为 .16. 在中, , , 将绕点按逆时针旋转,旋转角为()得到 , 与对应,与对应,则线段长度的取值范围为 .
15. 在中,为锐角,为的高,且 , 则的大小为 .16. 在中, , , 将绕点按逆时针旋转,旋转角为()得到 , 与对应,与对应,则线段长度的取值范围为 .三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.
-
17. 解方程组:18. 解不等式组:19. 如图,在中,点在边上,点在边上,连接 , , 已知 , , , 且 , 求的度数.
对于上述问题,在以下解答过程中的空白处填上适当的内容(理由或数学式).
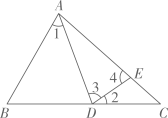
解:在中,( ),
, (已知),
∴ ▲ (等量代换),
∵(已知),
∴(等量代换),
在中,(三角形内角和等于180°),
又∵( ),
∴(等式的性质),
∵( ),
∴(等量代换)
20. 如图, , , 三点均在的正方形网格格点上(图中网格线的交点就是格点).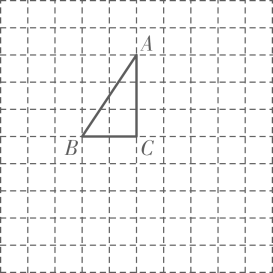
⑴画出将向右平移4格,再向下平移4格后的;
⑵画出将绕点顺时针旋转180°后的;
⑶在(1)和(2)的条件下,四边形是否为中心对称图形?若是,请在图中标出它的对称中心;若不是,请用所学知识简要说朋理由.
21. 妈妈:“今天在超市购物共花了几十块钱,且刚好是整数.但在使用微信支付时,不小心在个位数与十位数之间多按了一个小数点,结果再补支付了45.6元.”女儿:“妈妈,您是在考我吗?补支付的钱数一定不是45.6元.”
妈妈:“补支付的钱数只有一位小数位,我只说错了十分位上的数字,且十分位上的数字肯定不是0.”
(1)、你认为女儿的判断正确吗?妈妈这次购物是否超过50元?请直接写出你的判断结果;(2)、设妈妈购物花了元,补支付的钱数的十分位上的数字为 . 根据以上信息,求的值.22. 已知关于 , 的方程组其中为任意有理数.(1)、试说明:代数式的值不会随着的值的变化而变化:(2)、若 , 求的取值范围.23. 如图,在四边形中, , 分别平分和 , 与相交于点 , 延长 , 交于点 . (1)、已知 , 求的度数;(2)、若 , , , 试探究 , , 三者之间的等量失系.24. 在中国进出口商品交易会上,某陶瓷企业出售了 , , 三种产品.已知出售1件产品和2件产品共收入900元,出售2件产品和3件产品共收入1600元.(1)、求产品和产品的单价;(2)、若出售 , 两种产品(均有销售)共收入2400元,则出售 , 两种产品各几件?(3)、为推广产品,该企业开展促销活动:每出售一件产品,赠送2件产品.某客户欲购买 , , 三种产品共50件,并要求产品的件数是产品的1.5倍,产品至少10件.企业赠送的产品不能满足客户的需求,客户还需要另行购买部分产品,若产品单价为100元,求客户支付的总金额.25. 如图,将线段平移得到 , 使与对应,与对应,连接 , .
(1)、已知 , 求的度数;(2)、若 , , , 试探究 , , 三者之间的等量失系.24. 在中国进出口商品交易会上,某陶瓷企业出售了 , , 三种产品.已知出售1件产品和2件产品共收入900元,出售2件产品和3件产品共收入1600元.(1)、求产品和产品的单价;(2)、若出售 , 两种产品(均有销售)共收入2400元,则出售 , 两种产品各几件?(3)、为推广产品,该企业开展促销活动:每出售一件产品,赠送2件产品.某客户欲购买 , , 三种产品共50件,并要求产品的件数是产品的1.5倍,产品至少10件.企业赠送的产品不能满足客户的需求,客户还需要另行购买部分产品,若产品单价为100元,求客户支付的总金额.25. 如图,将线段平移得到 , 使与对应,与对应,连接 , .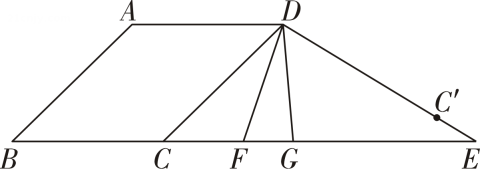 (1)、求证:;(2)、点在的延长线上,点与关于直线对称,直线交的延长线于点 . 点在线段上,且 .
(1)、求证:;(2)、点在的延长线上,点与关于直线对称,直线交的延长线于点 . 点在线段上,且 .①设 , 求的度数(用含的代数式表示);
②证明: .