浙江省杭州市萧山区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个几何图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式中，正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt{6} = 3$ C、 $\sqrt{4} = 2$ D、 $\sqrt{(- 4) \times (- 9)} = \sqrt{- 4} \times \sqrt{- 9}$

查看试题解析
3. 方程 $x^{2} = 5 x$ 的根是（）

A、 $x = 5$ B、 $x = 0$ C、 $x_{1} = 0$ ， $x_{2} = - 5$ D、 $x_{1} = 0$ ， $x_{2} = 5$

查看试题解析
4. 某校举行“喜迎二十大”党史知识竞赛，如图是10名决赛选手的成绩，对于这10名选手的成绩，下列说法中正确的是（）

A、众数是5 B、众数是2 C、中位数是95 D、中位数是90

查看试题解析
5. 如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（）

A、6 B、7 C、8 D、9

查看试题解析
6. 用反证法证明“一个三角形中最多有一个角为直角”时，应先作出的假设是（）

A、一个三角形中至少有两个角为直角 B、一个三角形中没有一个角为直角 C、一个三角形中至少有两个角为锐角 D、一个三角形中至少有两个角为钝角

查看试题解析
7. 如图，点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心， $B C 、 A B$ 长为半径画弧，两弧交于点D，分别连接 $A B 、 A D 、 C D$ ，则四边形 $A B C D$ 是平行四边形．其依据是（）

A、一组对边平行且相等的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、两组对边分别平行的四边形是平行四边形 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
8. 2022年底，新冠疫情持续蔓延，若一人携带病毒未进行有效隔离，经过两轮传染后共有441人感染，设每轮传染中平均每个人传染了 $x$ 人，则根据题意可列出方程（）

A、 $x (1 + x) = 441$ B、 $x + {(1 + x)}^{2} = 441$ C、 $x + x (1 + x) = 441$ D、 $1 + x + x (1 + x) = 441$

查看试题解析
9. 已知，点 $P (a ， b)$ 在反比例函数 $y = - \frac{6}{x}$ 的图象上，则下列结论正确的是（）

A、y随x的增大而增大 B、y随x的增大而减小 C、当 $a > - 1$ 时，则 $b > 6$ D、当 $a < - 1$ 时，则 $0 < b < 6$

查看试题解析
10. 如图， $△ A B C$ 是锐角三角形， $E$ 是 $B C$ 的中点，分别以 $A B$ ， $A C$ 为边向外侧作等腰三角形 $A B M$ 和等腰三角形 $A C N$ ．点 $D$ ， $F$ 分别是底边 $B M$ ， $C N$ 的中点，连接 $D E$ ， $E F$ ，若 $∠ B A M = ∠ C A N = θ$ （是锐角），则 $∠ D E F$ 的度数是（）

A、 $180 - 2 θ$ B、 $180 - θ$ C、 $90 + 2 θ$ D、 $90 + θ$

查看试题解析

二、填空题

11. 若代数式 $\sqrt{x - 2023}$ 有意义，则x的取值范围式.

查看试题解析
12. 甲、乙、丙、丁四名同学进行跳远测试，每人 $10$ 次跳远成绩的平均数都是 $2.68 m$ ，方差分别是 $S_{甲}^{2} = 1.60$ ， $S_{乙}^{2} = 1.62$ ， $S_{丙}^{2} = 0.58$ ， $S_{丁}^{2} = 0.45$ ，则这四名同学跳远成绩最稳定的是．

查看试题解析
13. 关于 $x$ 的一元二次方程 $x^{2} + a x - 1 = 0$ 的根的情况为．

查看试题解析
14. 如图，在 $▱ A B C D$ 中，对角线 $A C$ ， $B D$ 交于点 $E$ ， $A C ⊥ B C$ ．若 $A C = 2$ ， $A B = 3$ ，则 $B D =$ ．

查看试题解析
15. 如图， $C ， C_{1} ， C_{2} ， C_{3}$ 四个点在第一象限内，分别过这四个点作x轴的垂线 $C B ， C_{1} B_{1} ， C_{2} B_{2} ， C_{3} B_{3}$ 作y轴的垂线 $C A ， C_{1} A_{1} ， C_{2} A_{2} ， C_{3} A_{3}$ ，若矩形 $A O B C ， A_{1} O B_{1} C_{1} ， A_{2} O B_{2} C_{2} ， A_{3} O B_{3} C_{3}$ 的面积都是5，则 $C ， C_{1} ， C_{2} ， C_{3}$ 四个点所在的函数解析式为．

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A D = 2$ ，点P在 $C D$ 上，不与点C，点D重合，连接 $A P$ ， $B P$ ， $△ A B P$ 为直角三角形，当满足条件的P点有且只有一个时， $A B =$ ．

查看试题解析

三、解答题

17. 解方程：

(1)、 $3 y^{2} - 27 = 0$ ；

(2)、 $2 x (x - 1) + x = 1$ ．

查看试题解析
18. 如图1，放在墙角的立柜的上下底面是等腰直角三角形，如图2所示，若腰长 $A C$ 为1m，现要将这个立柜搬过宽为0.8m的通道，你觉得能通过吗？请说明理由．

查看试题解析
19. 某班开展一次综合与实践活动，部分记载如下：
【活动主题】利用树叶的特征对树木进行分类．
【实践过程】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如表：

1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【问题解决】

(1)、同学们通过计算得到芒果树叶的长宽比的平均数是3.74，请你继续计算出荔枝树叶的长宽比的平均数；

(2)、从树叶的长宽比的平均数来看，现有一片长13cm，宽6.5cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

查看试题解析
20. 已知，视力表上视力值 $V$ 和字母 $E$ 的宽度 $a$ （mm）之间的关系是我们已经学过的一类函数模型，字母 $E$ 的宽度 $a$ 如图1所示，经整理，视力表上部分视力值 $V$ 和字母 $E$ 的宽度 $a$ （mm）的对应数据如表所示：
位置
视力值 $V$
$a$ 的值（mm）
第1行
0.1
70
第5行
0.25
28
第8行
0.5
14
第14行
2.0
3.5

(1)、请你根据表格数据判断并求出视力值 $V$ 和字母 $E$ 的宽度 $a$ （mm）之间的函数表达式，并说明理由；

(2)、经过测量，第4行和第7行两行首个字母E的宽度a（mm）的值分别是35mm和17.5mm，求第4行、第7行的视力值．

查看试题解析
21. 已知：如图，将矩形纸片 $A B C D$ 的两个角分别沿 $B E$ ， $D F$ 向内折起，恰好使点A和点C落在对角线BD上同一点O处．

(1)、判断四边形 $B F D E$ 的形状，并说明理由；

(2)、若 $A B = 1$ ，求四边形 $B F D E$ 的面积．

查看试题解析
22. 已知，一辆汽车在笔直的公路上刹车后，该车的速度 $v ($ 米 $/$ 秒 $)$ 与时间 $t ($ 秒 $) (0 < t \leq 15)$ 之间满足一次函数关系，其图象如图所示；

(1)、求 $v$ 与 $t$ 之间的函数关系式；

(2)、已知汽车在该运动状态下，一段时间内向前滑行的距离等于这段时间内的平均速度乘以时间 $($ 该运动状态下的平均速度 $v =$ $\frac{v_{1} + v_{2}}{2}$ ， $v_{1}$ 表示这段时间起始时刻的速度， $v_{2}$ 表示这段时间结束时刻的速度 $)$ ．若该车刹车后 $t$ 秒内向前滑行了 $378$ 米，求 $t$ 的值．

查看试题解析
23. 如图，在正方形 $A B C D$ 中，点G在对角线 $B D$ 上，不与点B，D重合，连接 $A G$ 并延长交 $C D$ 于点E，连接 $C G$ 并延长交 $A D$ 于点M，过点D作 $D N ⊥ A E$ 交 $C M$ 于点P，交 $B C$ 于N，垂足为F．

(1)、求证： $A G = C G$ ；

(2)、求证： $∠ C G E = 2 ∠ B D N$ ；

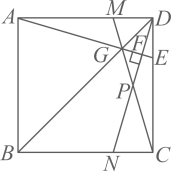(3)、若 $B D = 4 D G$ ， $G P = a$ ，求 $A G$ 的长．（用含a的式子表示）

查看试题解析

	1	2	3	4	5	6	7	8	9	10
芒果树叶的长宽比	3.8	3.7	3.5	3.4	3.8	4.0	3.6	4.0	3.6	4.0
荔枝树叶的长宽比	2.0	2.0	2.0	2.4	1.8	1.9	1.8	2.0	1.3	1.9

位置	视力值 $V$	$a$ 的值（mm）
第1行	0.1	70
第5行	0.25	28
第8行	0.5	14
第14行	2.0	3.5