浙江省杭州市西湖区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-20 类型:期末考试
一、单选题
-
1. 化简:( )A、 B、2 C、 D、42. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、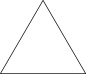 C、
C、 D、
D、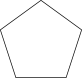 3. 方程的解是( )A、 B、 C、 , D、 ,4. 一组数据2,2,2,3,4,7,8,若加入一个整数 , 一定不会发生变化的统计量是( )A、众数 B、平均数 C、中位数 D、方差5. 若反比例函数的图象过点 , 则该图象必经过第( )象限A、一、三 B、二、四 C、一、二 D、三、四6. 如图,在四边形中,对角线 , 相交于点 , 且 , , 下列结论不一定成立的是( )
3. 方程的解是( )A、 B、 C、 , D、 ,4. 一组数据2,2,2,3,4,7,8,若加入一个整数 , 一定不会发生变化的统计量是( )A、众数 B、平均数 C、中位数 D、方差5. 若反比例函数的图象过点 , 则该图象必经过第( )象限A、一、三 B、二、四 C、一、二 D、三、四6. 如图,在四边形中,对角线 , 相交于点 , 且 , , 下列结论不一定成立的是( )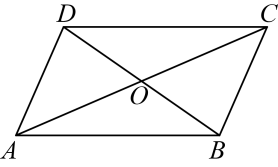 A、 B、 C、 D、7. 随着科技水平的提高,某种电子产品的价格呈下降趋势,今年年底的价格是两年前价格的 . 这种电子产品的价格在这两年中平均每年下降百分之几?( )A、25% B、37.5% C、50% D、75%8. 如图,点是正方形对角线上一点,点在上且 , 连接 , , 若 , , 则( )
A、 B、 C、 D、7. 随着科技水平的提高,某种电子产品的价格呈下降趋势,今年年底的价格是两年前价格的 . 这种电子产品的价格在这两年中平均每年下降百分之几?( )A、25% B、37.5% C、50% D、75%8. 如图,点是正方形对角线上一点,点在上且 , 连接 , , 若 , , 则( )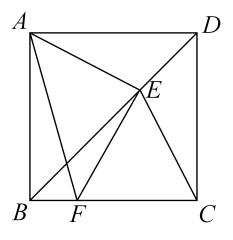 A、 B、 C、 D、9. 已知点 , , 在反比例函数的图象上, , 则下列结论一定成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 如图,在矩形中, , 连接 , , 与对角线交于点 , 且 , , 有下列三个结论:①;②;③ . 其中,正确的是( )
A、 B、 C、 D、9. 已知点 , , 在反比例函数的图象上, , 则下列结论一定成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 如图,在矩形中, , 连接 , , 与对角线交于点 , 且 , , 有下列三个结论:①;②;③ . 其中,正确的是( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 计算: .12. 五边形的内角和是度.13. 已知关于x的一元二次方程 有一解为0,则k的值等于.14. 对甲、乙两位同学近六次数学测试成绩进行统计分析,已知甲测试成绩的方差是 , 甲的成绩比乙的成绩更稳定,则乙测试成绩的方差可能是(写出一个即可).15. 已知一次函数和反比例函数的图象同时经过点 , 则的值是 .16. 如图,在正方形中, , 点是的中点,连结 , 则;点F在边AB上,将△BCF沿CF折叠,点B恰好落在CE上的点G处,连结EF,则 .

三、解答题
-
17. 计算: , 圆圆的做法是 .
圆圆的解答正确吗?如果不正确,请写出正确的解答过程.
18. 已知关于x的一元二次方程有两个不相等的实数根.(1)、求k的取值范围.(2)、当k取最大整数值时,求该方程的解.19. 某一家工程咨询公司技术部门员工一月份的工资报表如下:总工程师
工程师
工程师助理
技术员
客服
月收入(千元)
18
13
10
9
5
人数(人)
1
2
2
4
2
(1)、分别求该公司技术部门员工一月份工资的平均数、中位数和众数.(2)、二月初,一位员工辞职了,若其他员工的月收入不变,部门的平均收入升高了,你认为辞职的可能是哪个岗位上的员工?此时部门的平均收入升高了多少千元?(选一种说明即可)20. 如图,利用已有的一面长为的墙,用篱笆围一个面积为的矩形花圃 . 设的长为 , 的长为 . (1)、求y关于x的函数表达式和自变量x的取值范围.(2)、边和的长都是整数,若围成的矩形花圃的三边篱笆的总长不超过 , 试求出满足条件且用料最省的方案.21. 如图,在中, , 点是的中点,连结并延长,交的延长线于点 , 连结 , .
(1)、求y关于x的函数表达式和自变量x的取值范围.(2)、边和的长都是整数,若围成的矩形花圃的三边篱笆的总长不超过 , 试求出满足条件且用料最省的方案.21. 如图,在中, , 点是的中点,连结并延长,交的延长线于点 , 连结 , . (1)、求的长.(2)、若 ,
(1)、求的长.(2)、若 ,①证明:四边形是菱形.
②若 , 求四边形的周长.