安徽省亳州市谯城区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数没有平方根的是（）

A、 $- 2.5$ B、0 C、 $2.1$ D、6

查看试题解析
2. 要使分式 $\frac{4 + x}{4 - 2 x}$ 有意义，则 $x$ 应满足的条件是（）

A、 $x > - 2$ B、 $x < - 2$ C、 $x \neq 2$ D、 $x \neq - 2$

查看试题解析
3. “接天莲叶无穷碧，映日荷花别样红．”已知荷花粉的直径大约为 $0.0025$ 米．数据 $0.0025$ 用科学记数法表示为（）

A、 $0.25 \times 1 0^{- 3}$ B、 $2.5 \times 1 0^{- 3}$ C、 $25 \times 1 0^{- 1}$ D、 $2.5 \times 1 0^{3}$

查看试题解析
4. 下列算式中，结果等于 $4 m^{4}$ 的是（）

A、 $2 m^{2} + 2 m^{2}$ B、 $3 m^{2} \cdot m^{2}$ C、 $m^{5} \div 4 m$ D、 ${(- 2 m^{2})}^{2}$

查看试题解析
5. 不等式 $\frac{1}{2} (x + 3) \leq 3$ 的最大正整数解是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 解分式方程 $\frac{x}{3 - x} - 4 = \frac{6}{x - 3}$ 时，去分母正确的是（）

A、 $x - 4 = 6$ B、 $x - 4 (3 - x) = - 6$ C、 $x - 2 (x - 3) = 6$ D、 $x - 3 x - 4 = - 6$

查看试题解析
7. 如图，数轴上表示1， $\sqrt{2}$ 的点分别为A，B，点A是 $B C$ 的中点，则点C所表示的数是（）

A、 $\sqrt{2} - 1$ B、 $1 - \sqrt{2}$ C、 $2 - \sqrt{2}$ D、 $\sqrt{2} - 2$

查看试题解析
8. 如图，直线 $A B$ ， $C D$ 交于点 $O$ ， $O E ⊥ C D$ 于点 $O$ ．若 $∠ A O E = 110 °$ ，则 $∠ B O D$ 的度数为（）

A、 $40 °$ B、 $35 °$ C、 $30 °$ D、 $20 °$

查看试题解析
9. 如图，下列说法正确的是（）

A、若 $∠ A D E = ∠ B C D$ ，则 $A B ∥ C E$ B、若 $∠ A D B = ∠ C B D$ ，则 $A B ∥ C E$ C、若 $∠ A D C + ∠ B C D = 180 °$ ，则 $A B ∥ C E$ D、若 $∠ B A C = ∠ A C D$ ，则 $A B ∥ C E$

查看试题解析
10. 若实数 $a$ 使关于 $x$ 的不等式组 ${\begin{array}{l} 2 x + 3 > 3 x - 1 \\ 6 x - a \geq 2 x + 2 \end{array}$ 有且只有三个整数解，且使关于 $y$ 的方程 $\frac{y + a}{y - 1} + \frac{2 a}{1 - y} = 2$ 的解为非负数，则符合条件的整数 $a$ 的最大值为（）

A、 $- 2$ B、2 C、0 D、1

查看试题解析

二、填空题

11. 分解因式： $4 m - m a^{2} =$ ．

查看试题解析
12. 要使 $(y + 3) (y^{2} - m y - 2)$ 的展开式中不含 $y^{2}$ 项，则 $m$ 的值为．

查看试题解析
13. 若关于 $x$ 的不等式 $a x - b > 0$ 的解集是 $x < \frac{1}{3}$ ，则关于 $x$ 的不等式 $(a - b) x - (a + b) > 0$ 的解集为．

查看试题解析
14. 三角形 $A B C$ 和三角形 $A D E$ 是一副直角三角板，按如图方式摆放， $∠ B A C = ∠ D A E = 90 °$ ， $∠ C = 30 °$ ， $∠ E = 45 °$ ．

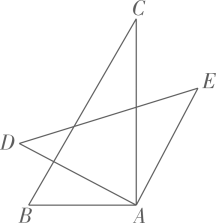(1)、若 $B C ⊥ A D$ ，则 ∠CAD 的度数为；

(2)、若将三角形 $A D E$ 绕点A动，使得两个直角三角形的斜边平行，则 $∠ D A C$ 的度数为．

查看试题解析

三、解答题

15. 计算： ${(\frac{1}{3})}^{- 2} - {(\sqrt{5} - 1)}^{0} - \sqrt[3]{- 8}$ ．

查看试题解析
16. 如图，若 $∠ 1 = ∠ 2$ ， $∠ 3 + ∠ 4 = 180 °$ ，试说明 $∠ B$ 与 $∠ B D C$ 之间的数量关系，并说明理由．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 2 x - 7 < 3 (x - 1) \\ 5 - \frac{1}{2} (x + 4) ⩾ x \end{array}$ ，并将解集在数轴上表示出来．

查看试题解析
18. 如图，在正方形网格中，每个小正方形的边长均为1个单位长度， $△ A B C$ 的三个顶点都在网格顶点处．现将 $△ A B C$ 平移得到 $△ A^{'} B^{'} C^{'}$ ，使点 $A$ 的对应点为点 $A^{'}$ ，点 $B$ 的对应点为点 $B^{'}$ ．

(1)、请画出平移后的 $△ A^{'} B^{'} C^{'}$ ；

(2)、若连接 $A A^{'}$ ， $C C^{'}$ ，则这两条线段之间的位置关系是，数量关系是．

查看试题解析
19. 观察下列等式：
第1个等式： $\frac{1}{1 + 2} + \frac{2}{1^{2} + 2 \times 1} = \frac{1}{1}$ ；

第2个等式： $\frac{1}{2 + 2} + \frac{2}{2^{2} + 2 \times 2} = \frac{1}{2}$ ；

第3个等式： $\frac{1}{3 + 2} + \frac{2}{3^{2} + 2 \times 3} = \frac{1}{3}$ ；

第4个等式： $\frac{1}{4 + 2} + \frac{2}{4^{2} + 2 \times 4} = \frac{1}{4}$ ；

……

按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第 $n$ 个等式（用含 $n$ 的式子表示， $n$ 为正整数），并说明等式成立的理由．

查看试题解析
20. 数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们进行推理，获得结论．初中数学里的一些代数恒等式，很多都可以借助几何图形进行直观推导和解释．请结合相关知识，解答下列问题：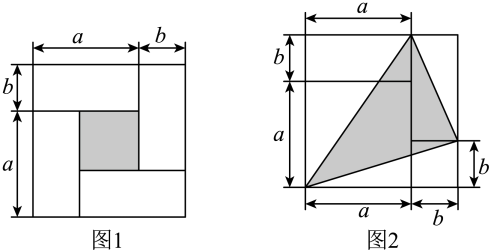

(1)、如图1是由4个大小相同，长为a、宽为b的长方形围成的边长为 $(a + b)$ 的正方形，用含字母a，b的代数式表示出阴影部分的面积．
①通过计算阴影部分正方形的边长，求阴影部分的面积，可列代数式：；
②通过用较大正方形的面积减去4个小长方形的面积，求阴影部分的面积，可列代数式：；

(2)、根据图1中的阴影部分的面积关系写出一个代数恒等式：；

(3)、若 $a + b = 6$ ， $a b = 8$ ，求图2中阴影部分的面积．

查看试题解析
21. 如果两个分式 $P$ 与 $Q$ 的和为常数 $m$ ，且 $m$ 为正整数，则称 $P$ 与 $Q$ 互为“完美分式”，常数 $m$ 称为“完美值”，如分式 $P = \frac{x}{x + 1}$ ， $Q = \frac{1}{x + 1}$ ， $P + Q = \frac{x + 1}{x + 1} = 1$ ，则 $P$ 与 $Q$ 互为“完美分式”，“完美值” $m = 1$ ．

(1)、已知分式 $A = \frac{x - 1}{x - 4}$ ， $B = \frac{x - 7}{x - 4}$ ，判断A与B是否互为“完美分式”？若不是，请说明理由；若是，请求出“完美值” $m$ ；

(2)、已知分式 $C = \frac{3 x - 4}{x - 2}$ ， $D = \frac{E}{x^{2} - 4}$ ，若 $C$ 与 $D$ 互为“完美分式”，且“完美值” $m = 3$ ，其中 $x$ 为正整数，分式 $D$ 的值为正整数．
①求 $E$ 所代表的代数式；
②求 $x$ 的值．

查看试题解析
22. 某学生用品超市准备购进 $A$ ， $B$ 两种类型的文具袋进行销售，若每个 $A$ 型文具袋比每个 $B$ 型文具袋的进价少2元，且用800元购进 $A$ 型文具袋的数量与用1000元购进 $B$ 型文具袋的数量相同．

(1)、每个 $A$ 型， $B$ 型文具袋的进价分别是多少元？

(2)、设该超市购进 $B$ 型文具袋 $m$ 个．
①若购进 $A$ 型文具袋的数量比 $B$ 型文具袋的数量的3倍少50个，且购进 $A$ 型， $B$ 型文具袋的总数量不超过910个，该超市最多购进 $B$ 型文具袋多少个？

②在①的条件下，若 $A$ 型、 $B$ 型文具袋的售价分别是12元/个和15元/个，且将购进的 $A$ 型、 $B$ 型文具袋全部售出后，可使销售两种文具袋的总利润超过3795元，则该超市购进两种文具袋共有 ▲ 种方案．

查看试题解析
23. 已知直线 $A B ∥ C D$ ，点 $M$ ， $N$ 分别在直线 $A B$ ， $C D$ 上，点 $E$ 为平面内一点．

(1)、如图1，请说明 $∠ M E N = ∠ A M E + ∠ E N C$ ；

(2)、如图2， $∠ A M E = 30 °$ ， $E F$ 平分 $∠ M E N$ ， $N P$ 平分 $∠ E N C$ ， $E Q ∥ N P$ ，求 $∠ F E Q$ 的度数：

(3)、如图3，点 $G$ 为 $C D$ 上一点， $∠ A M N = 3 ∠ E M N$ ， $∠ G E K = 3 ∠ G E M$ ， $E H ∥ M N$ 交 $A B$ 于点 $H$ ，请探究 $∠ G E K$ ， $∠ B M N$ ， $∠ G E H$ 之间的数量关系．

查看试题解析