安徽省淮北市五校联考2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-20 类型:期末考试
一、单选题
-
1. 实数中,最小的是( )A、 B、0 C、 D、2. 如图,下列结论中错误的是( )
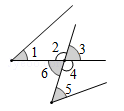 A、 与 是同旁内角 B、 与 是内错角 C、 与 是内错角 D、 与 是同位角3. 计算结果正确的是( )A、 B、 C、 D、4. 如果 ,那么下列不等式一定成立的是( )A、 B、 C、 D、5. 下列各式中,能用平方差公式分解因式的是( )A、 B、 C、 D、6. 如图, , 平分 , 且:: , 则的度数是( )
A、 与 是同旁内角 B、 与 是内错角 C、 与 是内错角 D、 与 是同位角3. 计算结果正确的是( )A、 B、 C、 D、4. 如果 ,那么下列不等式一定成立的是( )A、 B、 C、 D、5. 下列各式中,能用平方差公式分解因式的是( )A、 B、 C、 D、6. 如图, , 平分 , 且:: , 则的度数是( ) A、 B、 C、 D、7. 下列说法正确的是( )A、的算术平方根是 B、的平方根是 C、的算术平方根是 D、的立方根是8. 如图,一个宽度相等的纸条按如图所示方法折叠一下,则的度数( )
A、 B、 C、 D、7. 下列说法正确的是( )A、的算术平方根是 B、的平方根是 C、的算术平方根是 D、的立方根是8. 如图,一个宽度相等的纸条按如图所示方法折叠一下,则的度数( )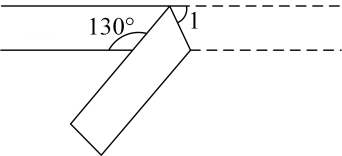 A、 B、 C、 D、9. 若关于x的分式方程有增根,则m的值为( )A、3 B、0 C、 D、10. 关于的多项式: , 其中为正整数,若各项系数各不相同且均不为0,我们称这样的多项式为“亲缘多项式”.
A、 B、 C、 D、9. 若关于x的分式方程有增根,则m的值为( )A、3 B、0 C、 D、10. 关于的多项式: , 其中为正整数,若各项系数各不相同且均不为0,我们称这样的多项式为“亲缘多项式”.①是“亲缘多项式”.
②若多项式和均为“亲缘多项式”,则也是“亲缘多项式”.
③多项式是“亲缘多项式”且 .
④关于的多项式 , 若 , , 为正整数,则为“亲缘多项式”.
以上说法中正确的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 如果分式有意义,那么实数x的取值范围是 .12. 如图,已知∠1=∠2,∠3=108°,则∠4= .
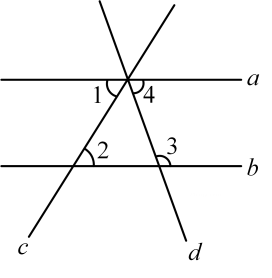 13. 如果是的两个平方根,那么 .14. 如图1所示,已知甲、乙为两把不同刻度的直尺,且同一把直尺上的刻度之间距离相等,小研将此两把直尺紧贴,并将两直尺上的刻度0彼此对准后,发现甲尺的刻度36会对准乙尺的刻度48.
13. 如果是的两个平方根,那么 .14. 如图1所示,已知甲、乙为两把不同刻度的直尺,且同一把直尺上的刻度之间距离相等,小研将此两把直尺紧贴,并将两直尺上的刻度0彼此对准后,发现甲尺的刻度36会对准乙尺的刻度48. (1)、如图2,若将甲尺向右平移且平移过程中两把直尺维持紧贴,使得甲尺的刻度0对准乙尺的刻度4,则此时甲尺的刻度21会对准乙尺的刻度是;(2)、如图3,若将甲尺向右平移且平移过程中两把直尺维持紧贴,使得甲尺的刻度0会对准乙尺的刻度m,如图3所示,则此时甲尺的刻度n会对准乙尺的刻度是 . (用含m,n的式子表示)
(1)、如图2,若将甲尺向右平移且平移过程中两把直尺维持紧贴,使得甲尺的刻度0对准乙尺的刻度4,则此时甲尺的刻度21会对准乙尺的刻度是;(2)、如图3,若将甲尺向右平移且平移过程中两把直尺维持紧贴,使得甲尺的刻度0会对准乙尺的刻度m,如图3所示,则此时甲尺的刻度n会对准乙尺的刻度是 . (用含m,n的式子表示)三、解答题
-
15. 计算:16. 如图,在由边长为的小正方形组成的网格中,给出了以格点网格线的交点为端点的线段 , 线段在网格线上.
 (1)、把线段向左平移个单位、再向上平移个单位,得到线段点与点是对应点,点与点是对应点在图中画出平移后的线段 .(2)、经过点的直线垂直于在图中画出直线直接写出:点到的距离是 .17. 解不等式 , 并把它的解集在数轴上表示出来.18. 先化简,再求值: , 其中 .19. 目前,“双师课堂”正成为教育界的一大热点.双师课堂的“双师”,指的是一位一线城市“名师”和一位当地城市“辅导教师”,上课模式为“名师”进行线上实时讲课,“辅导教师”在当地城市的线下课堂进行课堂管理,并对学生的学习状况进行跟进督导、巩固练习、批改作业等课堂服务.某校为响应号召,利用暑期在各班安装能够进行双师教学的设备.该校南楼安装的56台设备由甲队完成,北楼安装的32台设备由乙队完成.已知甲队的安装速度是乙队的2倍,且两队同时开工,甲队比乙队提前1天安装完成.甲、乙两队每天各安装多少台双师教学设备?20. 如图,直线相交于点 , .
(1)、把线段向左平移个单位、再向上平移个单位,得到线段点与点是对应点,点与点是对应点在图中画出平移后的线段 .(2)、经过点的直线垂直于在图中画出直线直接写出:点到的距离是 .17. 解不等式 , 并把它的解集在数轴上表示出来.18. 先化简,再求值: , 其中 .19. 目前,“双师课堂”正成为教育界的一大热点.双师课堂的“双师”,指的是一位一线城市“名师”和一位当地城市“辅导教师”,上课模式为“名师”进行线上实时讲课,“辅导教师”在当地城市的线下课堂进行课堂管理,并对学生的学习状况进行跟进督导、巩固练习、批改作业等课堂服务.某校为响应号召,利用暑期在各班安装能够进行双师教学的设备.该校南楼安装的56台设备由甲队完成,北楼安装的32台设备由乙队完成.已知甲队的安装速度是乙队的2倍,且两队同时开工,甲队比乙队提前1天安装完成.甲、乙两队每天各安装多少台双师教学设备?20. 如图,直线相交于点 , . (1)、已知 , 求的度数;(2)、如果是的平分线,那么是的平分线吗?请说明理由.21. 观察下列各图,寻找对顶角(不含平角)、邻补角.
(1)、已知 , 求的度数;(2)、如果是的平分线,那么是的平分线吗?请说明理由.21. 观察下列各图,寻找对顶角(不含平角)、邻补角.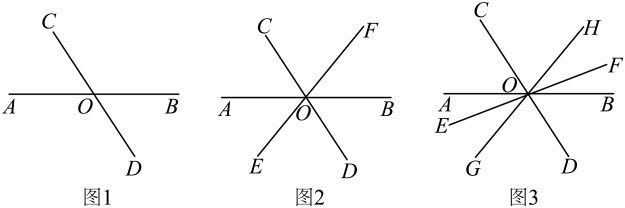 (1)、如图1,共有对对顶角,对邻补角;(2)、如图2,共有对对顶角,对邻补角;(3)、如图3,共有对对顶角,对邻补角;(4)、根据(1)-(3)中直线的条数与对顶角、邻补角的对数之间的关系,探究:若有条直线相交于一点,则可形成多少对对顶角?多少对邻补角?22. 在数轴上,点A表示的数为2,点B表示的数为5.(1)、如果C是数轴上的一点,那么点C到点A的距离与点C到点B的距离之和的最小值是 ;(2)、求关于x的不等式组的解集;(3)、如果关于x的不等式组的解集中每一个x值都不在线段AB上,求m的取值范围.23.(1)、如图1, , 为平面内一点, , 小颖认为若过点作 , 很容易说明和互余.请你帮小颖写出具体的思考过程.
(1)、如图1,共有对对顶角,对邻补角;(2)、如图2,共有对对顶角,对邻补角;(3)、如图3,共有对对顶角,对邻补角;(4)、根据(1)-(3)中直线的条数与对顶角、邻补角的对数之间的关系,探究:若有条直线相交于一点,则可形成多少对对顶角?多少对邻补角?22. 在数轴上,点A表示的数为2,点B表示的数为5.(1)、如果C是数轴上的一点,那么点C到点A的距离与点C到点B的距离之和的最小值是 ;(2)、求关于x的不等式组的解集;(3)、如果关于x的不等式组的解集中每一个x值都不在线段AB上,求m的取值范围.23.(1)、如图1, , 为平面内一点, , 小颖认为若过点作 , 很容易说明和互余.请你帮小颖写出具体的思考过程. (2)、如图2, , 点在射线上运动,当点运动到点与点之间时,试判断与 , 之间的数量关系,并说明理由;
(2)、如图2, , 点在射线上运动,当点运动到点与点之间时,试判断与 , 之间的数量关系,并说明理由; (3)、在(2)的条件下,当点在射线上的其他地方运动时(不与点重合),请直接写出与 , 之间的数量关系.
(3)、在(2)的条件下,当点在射线上的其他地方运动时(不与点重合),请直接写出与 , 之间的数量关系.