安徽省淮南市凤台县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-20 类型:期末考试
一、单选题
-
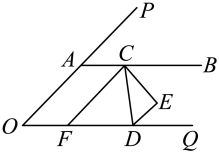
1. 下列各数没有平方根的是( )A、 B、0 C、3 D、4.12. 下列检测中,适宜采用普查方式的是( )A、检测―批药品的药效 B、检测一批日光灯的使用寿命 C、了解全国中学生每周的运动时间 D、检测“神舟十六号”载人飞船零件的质量3. 若点Q位于第三象限,点Q到x轴、y轴的距离均为3,则点Q的坐标为( )A、 B、 C、 D、4. 若不等式两边同时除以 , 则结果正确的是( )A、 B、 C、 D、5. 若 , 则m的取值范围是( )A、 B、 C、 D、6. 如图,直线交于点O,于点O.若 , 则的度数为( ).
 A、 B、 C、 D、7. 如图是中国象棋的一盘残局,如果用表示“帅”的位置,用表示“炮”的位置,那么“士”的位置应表示为( )
A、 B、 C、 D、7. 如图是中国象棋的一盘残局,如果用表示“帅”的位置,用表示“炮”的位置,那么“士”的位置应表示为( )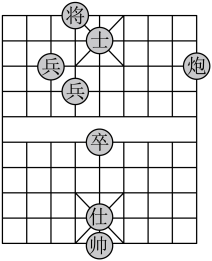 A、 B、 C、 D、8. 如图,将五个边长为1的小正方形组成的十字形纸板沿虚线剪开,把剪下的①放在②的位置,③放在④的位置,⑤放在⑥的位置,⑦放在⑧的位置,这样重新拼成一个大正方形,则大正方形的边长为( )
A、 B、 C、 D、8. 如图,将五个边长为1的小正方形组成的十字形纸板沿虚线剪开,把剪下的①放在②的位置,③放在④的位置,⑤放在⑥的位置,⑦放在⑧的位置,这样重新拼成一个大正方形,则大正方形的边长为( )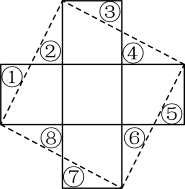 A、2 B、4 C、5 D、9. 已知 , 且 , 则k的取值范围是( )A、 B、 C、 D、10. 如图,直线 , 点P位于的右侧, , , 则下列命题错误的是( )
A、2 B、4 C、5 D、9. 已知 , 且 , 则k的取值范围是( )A、 B、 C、 D、10. 如图,直线 , 点P位于的右侧, , , 则下列命题错误的是( ) A、若 , 分别平分 , , 则 B、若点P是直线 , 之间的点,则 C、若点P是直线上方的点,则 D、若点P是直线下方的点,则
A、若 , 分别平分 , , 则 B、若点P是直线 , 之间的点,则 C、若点P是直线上方的点,则 D、若点P是直线下方的点,则二、填空题
-
11. 为了解某校七年级400名学生对电信诈骗知识的掌握情况,从中随机抽取40名学生进行问卷调查,此次调查中,样本容量是 .12. 两个完全相同的长方形按如图方式摆放成“L”形,则该图形的周长为 .
 13. 如图,点B,C,D都在直线l上,点A是直线外一点, . 若 , , , 则长的最小值为 .
13. 如图,点B,C,D都在直线l上,点A是直线外一点, . 若 , , , 则长的最小值为 . 14. 如图,某同学设计了一种计算流程图,据图完成下列问题:
14. 如图,某同学设计了一种计算流程图,据图完成下列问题: (1)、任意写出一个实数,使得该值经过一次运行就能输出结果,则该数为 .(2)、如果要使开始输入的x的值经过两次运行才能输出结果,那么x的整数值为 .
(1)、任意写出一个实数,使得该值经过一次运行就能输出结果,则该数为 .(2)、如果要使开始输入的x的值经过两次运行才能输出结果,那么x的整数值为 .三、解答题
-
15. 解不等式组:并将解集在数轴上表示出来.16. 如图,在平面直角坐标系中,的顶点都在网格点上,将先向右平移5个单位长度,再向下平移4个单位长度得到 .
 (1)、画出并直接写出 , , 的坐标﹔(2)、计算的面积.17. 《孙子算经》是我国古代重要的数学著作,其中有如下问题:今有人盗库绢,不知所失几何,但闻草中分绢,人得六匹,盈六匹;人得七匹,不足七匹.问人、绢各几何?大意是:有几个盗贼偷了仓库里的绢,不知道具体偷盗了多少匹绢,只听盗贼在草丛中分绢时说:“每人分6匹,会剩下6匹;每人分7匹,还差7匹.”问有多少盗贼?多少匹绢?18. 已知:如图 , , 度,度,求∠C的度数.
(1)、画出并直接写出 , , 的坐标﹔(2)、计算的面积.17. 《孙子算经》是我国古代重要的数学著作,其中有如下问题:今有人盗库绢,不知所失几何,但闻草中分绢,人得六匹,盈六匹;人得七匹,不足七匹.问人、绢各几何?大意是:有几个盗贼偷了仓库里的绢,不知道具体偷盗了多少匹绢,只听盗贼在草丛中分绢时说:“每人分6匹,会剩下6匹;每人分7匹,还差7匹.”问有多少盗贼?多少匹绢?18. 已知:如图 , , 度,度,求∠C的度数.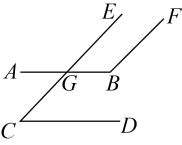 19. 若关于x,y的二元一次方程组与有公共的解.(1)、求x,y的值;(2)、求的值.20. 如图,在平面直角坐标系中,设一质点M自处向上运动1个单位至 , 然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,…,如此继续运动下去,设 , n=1,2,3,….
19. 若关于x,y的二元一次方程组与有公共的解.(1)、求x,y的值;(2)、求的值.20. 如图,在平面直角坐标系中,设一质点M自处向上运动1个单位至 , 然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,…,如此继续运动下去,设 , n=1,2,3,…. (1)、依次写出 , , , , , 的值;(2)、计算的值为;(3)、计算的值.21. 为了迎接中考体育考试,某校随机从九年级学生中抽取了a名学生进行跳绳模拟测试,其中跳绳按每分钟跳的次数计算,分成5个等次,并将跳绳测试成绩绘制成如下统计图、表(不完整).
(1)、依次写出 , , , , , 的值;(2)、计算的值为;(3)、计算的值.21. 为了迎接中考体育考试,某校随机从九年级学生中抽取了a名学生进行跳绳模拟测试,其中跳绳按每分钟跳的次数计算,分成5个等次,并将跳绳测试成绩绘制成如下统计图、表(不完整).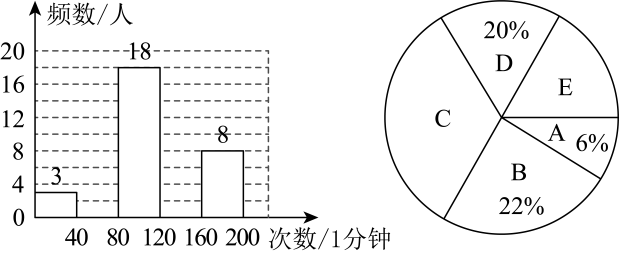
等次
跳绳次数/1分钟
A
B
C
D
E
根据以上信息,解答下列问题:
(1)、抽取的总人数 , 扇形统计图中“E”对应扇形的圆心角的大小为°;(2)、请补全频数分布直方图﹔(3)、成绩为C,D或E等次为合格,若该校九年级有3000人,请你估计该校九年级跳绳合格的人数.22. 某公司准备产品会展,需要进购―批盆景,已知有A,B两种款式的盆景,经统计发现,这两种盆景购买的价格表如下:A款式(盆)
B款式(盆)
总费用(元)
2
3
1020
3
4
1440
(1)、A,B两种款式的盆景每盆的价格分别是多少元?(2)、若该公司准备购进该盆景20盆,两种款式都要具有,并且至多准备资金3750元,请写出所有购买方案.23. 如图,是锐角,点A是边上一点,射线 . 已知三角板的两个锐角顶点分别落在和上, , .(1)、如图1,若 , 求的度数;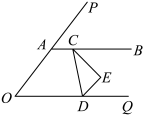 (2)、点F是上一点且平分 .
(2)、点F是上一点且平分 .①如图2,若 , 求证:;

②如图3,探索与之间的数量关系,并说明理由.