上海市徐汇区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-20 类型:期末考试
一、单选题
-
1. 下列实数中,无理数是( )A、 B、 C、 D、2. 月球沿着一定的轨道围绕地球运动,它在远地点时与地球相距约为405500千米,用科学记数法表示这个数(保留三个有效数字),那么下列表示正确的是( )A、 B、 C、 D、3. 已知三角形的两边长分别是2和5,那么下列选项中可以作为此三角形第三边长的是( )A、4 B、2 C、3 D、14. 在直角坐标系中,已知点P在第三象限内.且到x轴的距离为2,到y轴的距离为 , 那么点P的坐标是( )A、 B、 C、 D、5. 下列判断正确的是( )A、等腰三角形任意两角相等 B、等腰三角形底边上中线垂直底边 C、任意两个等腰三角形全等 D、等腰三角形三边上的中线都相等6. 如图,在中, , 点D在边上,如果 , 那么的大小是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 的平方根是8. .9. 比较大小:(填“”“”或“=”).10. 如果在数轴上的点到原点的距离是 , 那么表示点的实数是 .11. 已知点是线段上一点,过点作射线 , 如果比大 , 那么的度数是度.12. 已知中, , 点是边的中点,那么的度数是度.13. 已知点 , 那么它关于原点的对称点坐标为 .14. 如果点在第一象限,那么点在第象限.15. 如图,直线与直线相交于点 , , , 那么的度数是度.
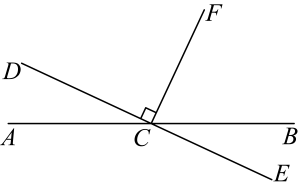 16. 如图,已知船在观测站的北偏东方向上,且在观测站的北偏西方向上,那么的度数是 .
16. 如图,已知船在观测站的北偏东方向上,且在观测站的北偏西方向上,那么的度数是 . 17. 如图,已知 , 点P是直线上的点, , , 那么的度数是度.
17. 如图,已知 , 点P是直线上的点, , , 那么的度数是度.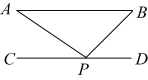 18. 如图,已知 , 如果要说明 , 那么还需要添加一个条件,这个条件可以是 .
18. 如图,已知 , 如果要说明 , 那么还需要添加一个条件,这个条件可以是 .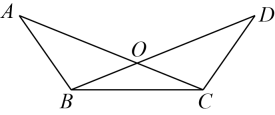 19. 如图,已知 , , , 那么的度数是 .
19. 如图,已知 , , , 那么的度数是 .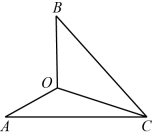 20. 在平面直角坐标系中,已知点 , 那么将点M绕原点O逆时针旋转后与点N重合,那么点N的坐标是 .
20. 在平面直角坐标系中,已知点 , 那么将点M绕原点O逆时针旋转后与点N重合,那么点N的坐标是 .三、解答题
-
21.(1)、计算: .(2)、利用分数指数幂的运算性质进行计算: .22. 如图,已知 , 根据下列要求作图并回答问题:
 (1)、作边上的高;(2)、过点D作直线的垂线,垂足为E;(3)、点B到直线的距离是线段的长度,(不要求写画法,只需写出结论即可)23. 在平面直角坐标系xOy中,的位置如图所示.
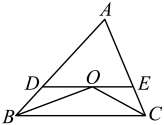
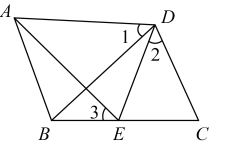
(1)、作边上的高;(2)、过点D作直线的垂线,垂足为E;(3)、点B到直线的距离是线段的长度,(不要求写画法,只需写出结论即可)23. 在平面直角坐标系xOy中,的位置如图所示.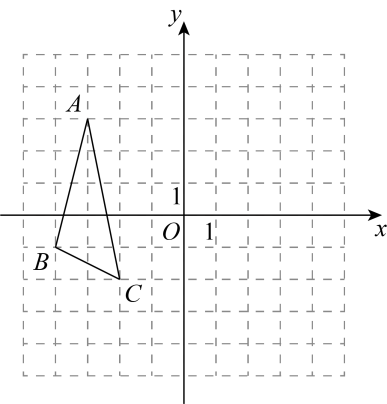 (1)、写出点A、B、C的坐标:A , B , C;(2)、画出关于y轴的对称图形;(3)、连接、 , 求的面积.24. 如图,点D是等边中边上的任意一点,且也是等边三角形,那么与平行吗?请说明理由.
(1)、写出点A、B、C的坐标:A , B , C;(2)、画出关于y轴的对称图形;(3)、连接、 , 求的面积.24. 如图,点D是等边中边上的任意一点,且也是等边三角形,那么与平行吗?请说明理由.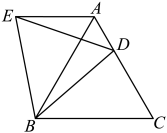
解:因为是等边三角形(已知),
所以(等边三角形各边相等),
(等边三角形每个内角都是);
因为是等边三角形(已知),
所以( ),
( );
所以( ),
所以 ▲ ▲ (等量减等量),
即∠ ▲ =∠ ▲ ;
在和中
所以( ).
所以 ▲ ( ),
所以 ,
所以 ,
所以( ).