安徽省宿州市萧县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-20 类型:期末考试
一、单选题
-
1. “疫情就是命令,防控就是责任”,面对疫情,各地积极普及科学防控知识.下面是科学防控知识图片,其中图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中是必然事件的是( )A、打开电视机,正在播放《新闻联播》 B、某种彩票中奖概率为1%,买100张该种彩票一定会有一张中奖 C、投掷一枚质地均匀的硬币100次,正面朝上的次数为50次 D、367个同学参加一个集会,他们中至少有两个同学的生日是同月同日3. 如图,已知则与∠1相等的角有( )
2. 下列事件中是必然事件的是( )A、打开电视机,正在播放《新闻联播》 B、某种彩票中奖概率为1%,买100张该种彩票一定会有一张中奖 C、投掷一枚质地均匀的硬币100次,正面朝上的次数为50次 D、367个同学参加一个集会,他们中至少有两个同学的生日是同月同日3. 如图,已知则与∠1相等的角有( ) A、1个 B、2个 C、3个 D、4个4. 王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段 AD 应该是 ABC 的( )
A、1个 B、2个 C、3个 D、4个4. 王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段 AD 应该是 ABC 的( ) A、角平分线 B、中线 C、高 D、任意一条线5. 如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于4的数的概率是( )
A、角平分线 B、中线 C、高 D、任意一条线5. 如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于4的数的概率是( )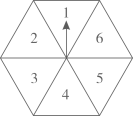 A、 B、 C、 D、6. 某学校劳动实践基地要围一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为24米,如图.设边的长为x米,边的长为y米,则y与x之间的关系式是( )
A、 B、 C、 D、6. 某学校劳动实践基地要围一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为24米,如图.设边的长为x米,边的长为y米,则y与x之间的关系式是( )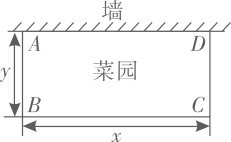 A、 B、 C、 D、7. 如图,在方形网格中,与有一条公共边且全等(不与重合)的格点三角形(顶点在格点上的三角形)共有( )
A、 B、 C、 D、7. 如图,在方形网格中,与有一条公共边且全等(不与重合)的格点三角形(顶点在格点上的三角形)共有( ) A、3个 B、4个 C、5个 D、6个8. 用直尺和圆规作一个角的平分线如图所示,说明∠AOC=∠BOC的依据是( ).
A、3个 B、4个 C、5个 D、6个8. 用直尺和圆规作一个角的平分线如图所示,说明∠AOC=∠BOC的依据是( ). A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等9. 如图,在中, , 是角平分线, , , 则P到的距离是( )
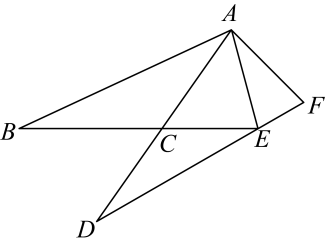
A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等9. 如图,在中, , 是角平分线, , , 则P到的距离是( ) A、2 B、3 C、4 D、510. 如图,在中, , 边的垂直平分线交于点D,交于点E,边的垂直平分线交于点F,交于点G,连接 , . 则的度数( )
A、2 B、3 C、4 D、510. 如图,在中, , 边的垂直平分线交于点D,交于点E,边的垂直平分线交于点F,交于点G,连接 , . 则的度数( )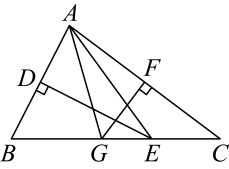 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3,理由是 .13. 如图,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③ACN≌ABM;④CD=DN.其中符合题意结论的序号是 .
 14. 如图,在锐角中, , , 的平分线交于点D,点M,N分别是和上的动点,则的最小值是 .
14. 如图,在锐角中, , , 的平分线交于点D,点M,N分别是和上的动点,则的最小值是 .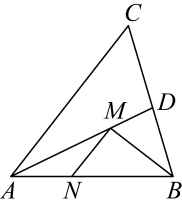
三、解答题
-
15. 计算:(1)、(2)、16. 如图, , 点E在上,求证: .
 17. 先化简,再求值: , 其中 .18. 某校举行“传颂中华家风,弘扬中华美德”演讲比赛.每班选拔一人参加.七年级(一)班的小丽和小华表现都很优秀,现在打算从2位同学中任选1人参加学校演讲比赛.为此设计了如下游戏规则:在一个不透明的袋子里装有10个除号码外其余都相同的小球,小球的号码分别是1,2,3,4,5,6,7,8,9,10.将它们充分摇匀,并从中任意摸出一个小球.规定摸出小球的号码能被3整除时,则小丽去;摸出小球的号码能被5整除时,则小华去.这个游戏对双方公平吗?请说明理由.如果不公平,应该如何修改游戏规则才能对双方公平?(游戏对双方公平的原则是双方获胜的概率相等).19. 如图,网格中每个小方格的边长为1,的顶点均在格点上.与关于直线l对称.
17. 先化简,再求值: , 其中 .18. 某校举行“传颂中华家风,弘扬中华美德”演讲比赛.每班选拔一人参加.七年级(一)班的小丽和小华表现都很优秀,现在打算从2位同学中任选1人参加学校演讲比赛.为此设计了如下游戏规则:在一个不透明的袋子里装有10个除号码外其余都相同的小球,小球的号码分别是1,2,3,4,5,6,7,8,9,10.将它们充分摇匀,并从中任意摸出一个小球.规定摸出小球的号码能被3整除时,则小丽去;摸出小球的号码能被5整除时,则小华去.这个游戏对双方公平吗?请说明理由.如果不公平,应该如何修改游戏规则才能对双方公平?(游戏对双方公平的原则是双方获胜的概率相等).19. 如图,网格中每个小方格的边长为1,的顶点均在格点上.与关于直线l对称. (1)、画出;(2)、求四边形的面积.20. 王师傅非常喜欢自驾游,他为了了解新买轿车的耗油情况,将油箱加满后进行了耗油试验,得到下表中的数据:
(1)、画出;(2)、求四边形的面积.20. 王师傅非常喜欢自驾游,他为了了解新买轿车的耗油情况,将油箱加满后进行了耗油试验,得到下表中的数据:行驶的路程
0
100
200
300
400
……
油箱剩余油量
50
42
34
26
18
……
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、这辆轿车油箱的容量是多少?当轿车行驶时,估计油箱中的剩余油量是多少?(3)、王师傅将油箱加满后驾驶该轿车从A地前往B地,到达B地时油箱中的剩余油量为 , 请求出A,B两地之间的路程.21. (1)、萧县某中学计划为学生暑期军训调配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 .(2)、图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿和的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度设计为 , 则由以上信息可推得的长度是多少?请说明理由.
(1)、萧县某中学计划为学生暑期军训调配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 .(2)、图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿和的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度设计为 , 则由以上信息可推得的长度是多少?请说明理由.