四川省达州市通川区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列计算一定正确的是（　　）

A、 $(a^{3})^{2} = a^{5}$ B、 $a^{3} \cdot a^{2} = a^{5}$ C、 $a^{3} + a^{2} = a^{5}$ D、 $a^{3} - a^{2} = a$

查看试题解析
3. 已知三角形的三边长分别是 $3$ ， $5$ ， $x$ ，则 $x$ 的取值不可能是（）

A、3 B、5 C、7 D、9

查看试题解析
4. 我国诺贝尔医学奖得主中国科学家屠呦呦，发现了一种病毒的长度约为 $0.00000456$ 毫米，则数据 $0.00000456$ 用科学记数法表示为（）

A、 $0.456 \times 1 0^{- 5}$ B、 $4.56 \times 1 0^{- 6}$ C、 $4.56 \times 1 0^{- 7}$ D、 $4.56 \times 1 0^{- 8}$

查看试题解析
5. 小华在如图所示的 $4 \times 4$ 正方形网格纸板上玩飞镖游戏（每次飞镖均落在纸板上，且落在纸板的任何一个点的机会都相等），则飞镖落在阴影区域的概率是（）

A、 $\frac{5}{16}$ B、 $\frac{1}{4}$ C、 $\frac{3}{8}$ D、 $\frac{7}{16}$

查看试题解析
6. 一列火车匀速通过一笔直隧道（隧道长大于火车的长），火车在隧道内的长度y与火车进入隧道的时间x之间的关系用图象描述正确的是（）

A、 B、 C、 D、

查看试题解析
7. 同一平面内， $∠ A$ 与 $∠ B$ 的两边互相平行， $∠ B$ 比 $∠ A$ 的2倍少 $30 °$ ，则 $∠ A$ 是（）

A、 $30 °$ B、 $70 °$ C、 $30 °$ 或 $50 °$ D、 $30 °$ 或 $70 °$

查看试题解析
8. 如图，在 $△ A B C$ 中，在边BC上取一点D，连接AD，在边AD上取一点E，连接CE．若 $△ A D B ≌ △ C D E$ ， $∠ B A D = α$ ，则 $∠ A C E$ 的度数为（）

A、 $α$ B、 $α - 45 °$ C、 $45 ° - α$ D、 $90 ° - α$

查看试题解析
9. 如图，正方形ABCD和长方形DEFG的面积相等，且四边形AEFH也为正方形.欧几里得在《几何原本》中利用该图得到了：AH²=AB×BH.设AB=a，BH=b.若ab=45，则图中阴影部分的周长为（）

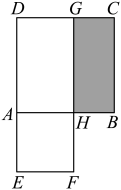A、25 B、26 C、28 D、30

查看试题解析
10. 李大爷以每千克 $2.1$ 元的价格批发了一批南瓜到镇上出售，为了方便，他带了一些零钱备用，他先按市场价售出一些后，由于滞销，然后他每千克降低 $1.6$ 元将剩余部分全部售出．他手中持有的钱数 $y$ 元（含备用零钱）与售出南瓜千克数 $x$ 的关系如图所示，下列说法中正确的有（）
①李大爷自带的零钱是 $50$ 元；②降价前他每千克南瓜出售的价格是 $3.6$ 元；③这批南瓜一共有 $160$ 千克；④李大爷销售这批南瓜一共赚了 $194$ 元．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知x^m＝20，xⁿ＝5，则x^m^-ⁿ＝．

查看试题解析
12. 已知 $(x - 3) (x + 8) = x^{2} + m x + n$ ，则 $m =$ ， $n =$ ．

查看试题解析
13. 一辆汽车邮箱内有油62升．如果设邮箱内剩油量为y（升），行驶路程为x（千米），则y随x的变化而变化：

行驶路程x（千米）

100

200

300

400

油箱内剩油量y（升）

50

38

26

14

请根据表格中的数据写出y（升）与x（千米）之间的关系式y= ．

查看试题解析
14. 一个正方形和两个等边三角形的位置如图所示，∠3=50°，则∠1+∠2=。

查看试题解析
15. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ B = 44 °$ ．点D是边 $A B$ 上一点，点B关于直线 $C D$ 的对称点为 $B ′$ ，当 $B^{'} D ∥ A C$ 时，则 $∠ B C D$ 的度数为．

查看试题解析

三、解答题

16. 计算：

(1)、 ${(2023 - π)}^{0} + {(- \frac{1}{2})}^{- 3} - {(- 1)}^{2023} + | - 3 |$ ；

(2)、先化简，再求值： $[{(2 x + 3 y)}^{2} - (2 x + y) (2 x - y)] \div (- 2 y)$ ，其中 $x = \frac{1}{3}$ ， $y = - \frac{1}{2}$ ．

查看试题解析
17. 已知，如图， $B C E$ 、 $A F E$ 是直线， $A B ∥ C D$ ， $A D ∥ B E$ ， $∠ 1 = ∠ 2$ ．求证： $∠ 3 = ∠ 4$ ．

查看试题解析

18. 为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（

x

分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：

分数段（分）	频数（人）	频率
$51 \leq x < 61$	$a$	0.1
$61 \leq x < 71$	18	0.18
$71 \leq x < 81$	$b$	$n$
$81 \leq x < 91$	35	0.35
$91 \leq x < 101$	12	0.12
合计	100	1

(1)、填空：

a =

，

b =

，

n =

；

(2)、将频数分布直方图补充完整；

(3)、该校对考试成绩为

91 \leq x \leq 100

的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数.

查看试题解析

19. 如图，正方形网格中每个小方格的边长为1，且点A，B，C均为格点．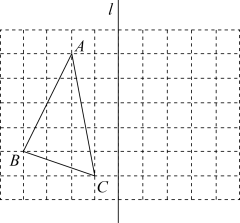

(1)、作图（保留作图痕迹，不写作法）：
①作出 $△ A B C$ 关于直线l的对称图形 $△ A^{'} B^{'} C^{'}$ ；
②在直线l上找一点D，使 $A D + B D$ 最小；

(2)、求出 $△ A^{'} B^{'} C^{'}$ 的面积．

查看试题解析
20. 一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，到达目的地后停止，设慢车行驶时间为 $x$ 小时，两车之间的距离为 $y$ 千米，两者的关系如图所示，根据图象探究：

(1)、看图填空：两车出发小时，两车相遇；

(2)、求快车和慢车的速度；

(3)、求线段 $B C$ 所表示的 $y$ 与 $x$ 的关系式，并求两车行驶 $6$ 小时两车相距多少千米．

查看试题解析
21. 已知a，b，c是 $△ A B C$ 的三条边长，且a，b，c是正整数．

(1)、若a，b，c满足 $(x + a) (x + b) = x^{2} + 17 x + 60$ ，且 $a^{2} + b^{2} = c^{2}$ ，求 $△ A B C$ 的周长；

(2)、若a，b，c满足 $a^{2} - 4 a b + 5 b^{2} - 6 b + 9 = 0$ ，且 $△ A B C$ 的周长是偶数，求c的值

查看试题解析
22. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $D$ 为 $A C$ 边上的一点，连接 $B D$ ， $E$ 为 $B D$ 上的一点，连接 $C E$ ， $∠ C E D = ∠ A B D$ ，过点 $A$ 作 $A G ⊥ C E$ ，垂足为 $G$ ， $A G$ 交 $E D$ 于点 $F$ ．

(1)、判断 $A F$ 与 $A D$ 之间的数量关系，并说明理由；

(2)、如图2，若 $A C = C E$ ， $D$ 为 $A C$ 的中点， $A B$ 与 $A C$ 相等吗？为什么？

查看试题解析
23. 如图， $R t △ A C B$ 中， $∠ A C B = 90 °$ ， $△ A B C$ 的角平分线 $A D$ 、 $B E$ 相交于点 $P$ ，过 $P$ 作 $P F ⊥ A D$ 交 $B C$ 的延长线于点 $F$ ，交 $A C$ 于点 $H$ ．

(1)、求 $∠ A P B$ 度数；

(2)、求证： $△ A B P$ ≌ $△ F B P$ ；

(3)、猜想线段 $A H$ ， $A B$ ， $B D$ 的数量关系，并证明．

查看试题解析
24. 如图，已知 $△ A B C$ 中， $A B = A C = 12$ 厘米， $∠ B = ∠ C$ ， $B C = 8$ 厘米，点D为 $A B$ 的中点，如果点P在线段 $B C$ 上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段 $C A$ 上由C点向A点运动．

(1)、若点Q的运动速度与点P的运动速度相等，经过1秒后， $△ B P D$ 与 $△ C Q P$ 是否全等？为什么？

(2)、若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能使 $△ B P D$ 与 $△ C Q P$ 全等？

查看试题解析

行驶路程x（千米）	100	200	300	400
油箱内剩油量y（升）	50	38	26	14