四川省成都市成华区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-20 类型:期末考试
一、单选题
-
1. 下列四个运动会会徽中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 我国古代数学家祖冲之推算出圆周率的近似值为 , 它与的误差小于 . 其中数据用科学记数法可以表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 已知三角形的两边长分别为5cm和8cm,则第三边的长可以是( )A、2cm B、3cm C、6cm D、13cm5. 下列事件是必然事件的是( )A、打开电视,正在播放神舟载人飞船发射 B、掷一枚骰子,点数是3的面朝上 C、两直线被第三条直线所截,同位角相等 D、三角形内角和是180°6. 如图,与 相交于点 O, , , 不添加辅助线,判定的依据是( )
2. 我国古代数学家祖冲之推算出圆周率的近似值为 , 它与的误差小于 . 其中数据用科学记数法可以表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 已知三角形的两边长分别为5cm和8cm,则第三边的长可以是( )A、2cm B、3cm C、6cm D、13cm5. 下列事件是必然事件的是( )A、打开电视,正在播放神舟载人飞船发射 B、掷一枚骰子,点数是3的面朝上 C、两直线被第三条直线所截,同位角相等 D、三角形内角和是180°6. 如图,与 相交于点 O, , , 不添加辅助线,判定的依据是( ) A、 B、 C、 D、7. 如图,直线 , 点 , 分别在 , 上,以点为圆心,长为半径画弧,交于点 , 连接 . 若 , 则的度数为( )
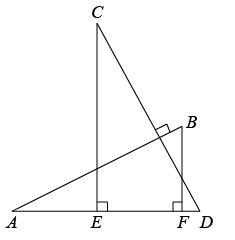
A、 B、 C、 D、7. 如图,直线 , 点 , 分别在 , 上,以点为圆心,长为半径画弧,交于点 , 连接 . 若 , 则的度数为( ) A、10° B、15° C、20° D、25°8. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
A、10° B、15° C、20° D、25°8. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若 , 则的值为 .10. 在一个不透明的口袋中装有红球和白球共16个,这些球除颜色外都相同,将口袋中的球搅匀后,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程.若共摸了100次球,发现有75次摸到红球,则可以估计口袋中红球的个数为 .11. 我们可以根据如图的程序计算因变量的值.若输入的自变量的值是2和时,输出的因变量的值相等,则的值为 .
 12. 如图,在中,分别以点 , 为圆心,大于的一半为半径作弧,两弧交于点 , , 直线交于点 , 连接 . 若 , , 则的周长等于 .
12. 如图,在中,分别以点 , 为圆心,大于的一半为半径作弧,两弧交于点 , , 直线交于点 , 连接 . 若 , , 则的周长等于 . 13. 如图,将长方形纸片沿直线折叠,点的对应点为点 , 与交于点 . 若 , 则的度数是 .
13. 如图,将长方形纸片沿直线折叠,点的对应点为点 , 与交于点 . 若 , 则的度数是 .
三、解答题
-
14.(1)、计算:;(2)、计算: .15.(1)、先化简,再求值: , 其中 , ;(2)、先化简,再求值: , 其中 , .16. 学校将举办主题为“爱成都・迎大运”知识竞赛活动,班决定在甲乙两人中选择一人参加,并采用如下游戏确定参加人员.如图,一个均匀的转盘被平均分成10等份,分别标有1,2,3,4,5,6,7,8,9,10这10个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.甲乙两人参与游戏:一人转动转盘,另一人猜数,若所猜数字与转出的数字相符,则猜数的人获胜,否则转动转盘的人获胜.猜数的方法从下面三种中选一种:①猜“是奇数”或“是偶数”;②猜“是3的倍数”或“不是3的倍数”;③猜“是大于6的数”或“不是大于6的数”.
如果由乙转动转盘,甲猜数,那么为了尽可能获胜,试说明甲应选择哪一种猜数方法?怎样猜?
 17. 《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2卷“几何与代数”部分,记载了很多利用几何图形来论证的代数结论.
17. 《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2卷“几何与代数”部分,记载了很多利用几何图形来论证的代数结论.如图,在中, , , , , 以为直角边在的右侧作等腰直角 , 其中 , , 过点作 , 垂足为点 .
 (1)、求证: , ;(2)、请你用两种不同的方法表示梯形的面积,并证明:;(3)、若 , , 求中边上的高 .18. 如图1,在等腰直角中, , 点是线段上不与点 , 重合的动点,连接并延长至点 , 使 , 过点作 , 垂足为点 .
(1)、求证: , ;(2)、请你用两种不同的方法表示梯形的面积,并证明:;(3)、若 , , 求中边上的高 .18. 如图1,在等腰直角中, , 点是线段上不与点 , 重合的动点,连接并延长至点 , 使 , 过点作 , 垂足为点 . (1)、当点 , 位于点的异侧时,问线段 , , 之间有何数量关系?写出你的结论并证明;(2)、当点 , 位于点的同侧时,若 , , 请在备用图中画出图形,并求的长.
(1)、当点 , 位于点的异侧时,问线段 , , 之间有何数量关系?写出你的结论并证明;(2)、当点 , 位于点的同侧时,若 , , 请在备用图中画出图形,并求的长.四、填空题
-
19. 计算: .20. 等腰三角形的两边长分别为3cm和6cm,这个等腰三角形的周长为cm.21. 如图是一束光线先后经平面镜 , 反射的示意图,若反射光线与入射光线平行,则的度数是 .
 22. 甲、乙二人在学校百米跑道上练习竞走,两人分别从跑道两端开始往返练习.二人离甲出发端的距离(米)与时间(秒)的关系如图所示.若两人均匀速练习了20分钟(不计转向时间),则二人迎面相遇的次数为 .
22. 甲、乙二人在学校百米跑道上练习竞走,两人分别从跑道两端开始往返练习.二人离甲出发端的距离(米)与时间(秒)的关系如图所示.若两人均匀速练习了20分钟(不计转向时间),则二人迎面相遇的次数为 . 23. 如图,在中, , , 点为上一动点,在上取点 , 使 , 连接 , , 当的值最小时,的度数为 .
23. 如图,在中, , , 点为上一动点,在上取点 , 使 , 连接 , , 当的值最小时,的度数为 .
五、解答题
-
24. 学校组织学生从学校出发,乘坐大巴车匀速前往卧龙大熊猫基地进行研学活动.大巴车出发0.5小时后,学校运送物资的轿车沿相同路线匀速前往.如图是大巴车行驶路程(千米)和轿车行驶路程(千米)随行驶时间(小时)变化的图象.请结合图象信息,解答下列问题:
 (1)、分别求出 , 与之间的关系式;(2)、问轿车追上大巴车时距离学校多远?25. 如图,在四边形中, , , 延长到点 , 是的平分线,是的平分线.
(1)、分别求出 , 与之间的关系式;(2)、问轿车追上大巴车时距离学校多远?25. 如图,在四边形中, , , 延长到点 , 是的平分线,是的平分线. (1)、如图1,当时,求证:;(2)、如图2,当时,直线交直线于点 , 问与 , 之间有何数量关系?写出你的结论并证明;(3)、如果将(2)中的条件改为 , 那么与 , 之间又有何数量关系?请直接写出结论,不用证明.26. 如图1,等边的边长为4,点是直线上异于 , 的一动点,连接 , 以为边长,在在侧作等边 , 连接 .
(1)、如图1,当时,求证:;(2)、如图2,当时,直线交直线于点 , 问与 , 之间有何数量关系?写出你的结论并证明;(3)、如果将(2)中的条件改为 , 那么与 , 之间又有何数量关系?请直接写出结论,不用证明.26. 如图1,等边的边长为4,点是直线上异于 , 的一动点,连接 , 以为边长,在在侧作等边 , 连接 . (1)、求证:;(2)、当点在直线上运动时,
(1)、求证:;(2)、当点在直线上运动时,①的周长是否存在最小值?若存在,求此时的长;若不存在,说明理由;
②能否形成直角三角形?若能,求此时的长;若不能,说明理由.