北师大版数学九年级上册同步练习——第四章《图形的相似》3.相似多边形

试卷更新日期：2023-07-20 类型：同步测试

进入出卷网下载

一、单选题

1. 任意下列两个图形不一定相似的是（）

A、正方形 B、等腰直角三角形 C、矩形 D、等边三角形

查看试题解析
2. 下列各组图形不是相似图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图所示的两个四边形相似，则下列结论不正确的是（）

A、 $a = 2 \sqrt{2}$ B、 $m = 2 n$ C、 $x = 2$ D、 $∠ α = 60 °$

查看试题解析
4. 下列图形中，不是相似图形的一组是（）

A、 B、 C、 D、

查看试题解析
5. 两个大小不一的五边形 $A B C D E$ 和五边形 $F B C H G$ 如图所示放置，点F在线段 $A B$ 上，点H在线段 $C D$ 上，对应连接并延长 $A F ， E G ， D H$ 刚好交于一点O，则这两个五边形的关系是（）

A、一定相似 B、一定不相似 C、不一定相似 D、不能确定

查看试题解析
6. 已知四边形ABCD∽四边形EFGH，且AB＝3，EF＝4，FG＝5.则四边形EFGH与四边形ABCD的相似比为（）

A、3：4 B、3：5 C、4：3 D、5：3

查看试题解析
7. 下列各组图形中一定相似的是（）.

A、两个直角三角形 B、两个等边三角形 C、两个菱形 D、两个矩形

查看试题解析
8. 如图，矩形ABCD∽矩形EFGH，已知 $A B = 3 cm$ ， $B C = 5 cm$ ， $E F = 6 cm$ ，则FG的长为（）

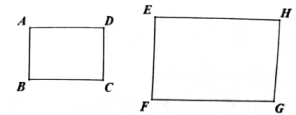A、8cm B、10cm C、12cm D、15cm

查看试题解析

二、填空题

9. 如图，矩形ABCD中，AB＝2，BC＝4，剪去一个矩形ABEF后，余下的矩形EFDC∽矩形BCDA，则EC的长为.

查看试题解析
10. 如图，把一个大长方形 $A B C D$ 划分成三个全等的小长方形，若每一个小长方形均与大长方形 $A B C D$ 相似，则 $A D ： C D$ 的值为.

查看试题解析
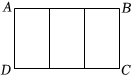11. 如图，将一张矩形纸片沿 $E F$ 折叠，得到两个全等的小矩形 $A B C D$ .如果矩形 $A B C D ∽$ 矩形 $A D F E$ ，那么 $\frac{A B}{A D}$ 的值是.

查看试题解析
12. 如图，四边形 $A B C D ∽$ 四边形 $A^{'} B^{'} C^{'} D^{'}$ ，若 $∠ B = 55 °$ ， $∠ C = 80 °$ ， $∠ A^{'} = 110 °$ ，则 $∠ D =$ °．

查看试题解析
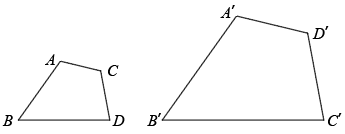13. 制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是元．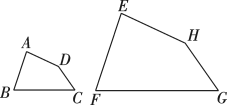

查看试题解析
14. 如图，四边形 $A B C D ∽$ 四边形 $E F G H$ ，若 $A B = 2$ ， $B C = 3$ ， $E F = 4$ ，则FG的长为．

查看试题解析

三、解答题

15. 如图，四边形ABCD∽四边形A₁B₁C₁D₁ ， ∠A＝80°，∠B＝75°，∠C＝125°，求x，∠D₁.

查看试题解析
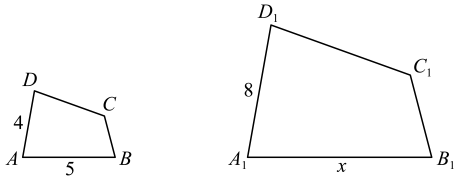16. 学生会要举办一个校园书画艺术展览会，为国庆献礼，小华和小刚准备将长AD为400cm，宽AB为130cm的矩形作品四周镶上彩色纸边装饰，如图所示，两人在设计时要求内外两个矩形相似，矩形作品面积是总面积的 $\frac{25}{36}$ ，他们一致认为上下彩色纸边要等宽，左右彩色纸边要等宽，这样效果最好，请你帮助他们设计彩色纸边宽度.

查看试题解析
17. 若四边形ABCD与四边形A₁B₁C₁D₁相似，相似比为k₁= $\frac{1}{2}$ ，又四边形A₁B₁C₁D₁与四边形A₂B₂C₂D₂相似，相似比为k₂= $\frac{3}{4}$ ，请问四边形ABCD与四边形A₂B₂C₂D₂相似吗？若相似，相似比是多少？

查看试题解析
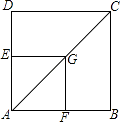
18. 如图，G是正方形ABCD对角线AC上一点，作GE⊥AD，GF⊥AB，垂足分别为点E，F．求证：四边形AFGE与四边形ABCD相似．

查看试题解析
19. 如图，把一个矩形 $A B C D$ 划分成三个全等的小矩形.

(1)、若原矩形 $A B C D$ 的长 $A B = 6$ ，宽 $B C = 4$ .问：每个小矩形与原矩形相似吗？请说明理由.

(2)、若原矩形的长 $A B = a$ ，宽 $B C = b$ ，且每个小矩形与原矩形相似，求矩形长 $a$ 与宽 $b$ 应满足的关系式.

查看试题解析
20. 为了铺设一矩形场地，特意选择某地砖进行密铺，为了使每一部分都铺成如图所示的形状，且由8块地砖组成，问：

(1)、每块地砖的长与宽分别为多少？

(2)、这样的地砖与所铺成的矩形地面是否相似？试明你的结论.

查看试题解析

北师大版数学九年级上册同步练习——第四章 《图形的相似》3.相似多边形

一、单选题

二、填空题

三、解答题

北师大版数学九年级上册同步练习——第四章《图形的相似》3.相似多边形