吉林省长春市榆树市八号镇2022-2023学年八年级下学期7月期末联考数学试题

试卷更新日期：2023-07-20 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共24分）

1. 五边形的内角和是（）

A、180° B、360° C、540° D、720°

查看试题解析
2. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{7}$ B、 $\sqrt{9}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
3. 由下列线段组成的三角形不是直角三角形的是（　　）

A、7，24，25 B、4，5， $\sqrt{41}$ C、3，5，4 D、4，5，6

查看试题解析
4. 下列各式成立的是（）

A、 $3 + 2 \sqrt{3} = 5 \sqrt{3}$ B、 $3 \sqrt{5} - \sqrt{5} = 3$ C、 $\sqrt{{(- 2)}^{2}} = 2$ D、 $\sqrt{12} \div \sqrt{6} = 2$

查看试题解析
5. 已知P₁（﹣1，y₁），P₂（2，y₂）是一次函数y=﹣x+1图象上的两个点，则y₁ ， y₂的大小关系是（）

A、y₁=y₂ B、y₁＜y₂ C、y₁＞y₂ D、不能确定

查看试题解析
6. 如图，直线y＝ax+b过点A（0，3）和点B（-2，0），则方程ax+b＝0的解是（）

A、x＝3 B、x＝0 C、x＝-2 D、x＝-3

查看试题解析
7. 在矩形ABCD中，对角线AC、BD相交于点O，∠BOC＝120°，AC＝6，则AB的长为（）

A、3 B、3 $\sqrt{3}$ C、6 D、6 $\sqrt{3}$

查看试题解析
8. 如图，菱形OABC的顶点C的坐标为（3，4），顶点A在x轴的正半轴上，反比例函数y＝ $\frac{k}{x}$ (x＞0)的图象经过顶点B，则k的值为（）

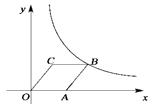A、12 B、20 C、24 D、32

查看试题解析

二、填空题（每题3分，共18分）

9. 计算： $(\sqrt{7} - 2)^{0}$ ＝．

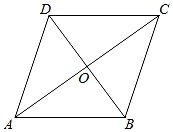
查看试题解析
10. 在函数y＝2x²+1中，当自变量x＝3时，因变量y的值是．

查看试题解析
11. 已知关于 $x$ 的方程 $\frac{1}{a x - 3} = \frac{1}{a - x}$ 有解 $x = 2$ ，则 $a$ 的值为．

查看试题解析
12. 小张到某建筑公司打工，公司承诺：正常上班的工资为150元/天，不能正常上班的工资为50元/天．如果某月（30天）正常上班的天数占80%，其余天数不能正常上班，则当月小张的日平均工资为元．

查看试题解析
13. 已知池中有 $600 m^{3}$ 的水，每小时抽 $50 m^{3}$ ，则剩余水的体积 $Q (m^{3})$ 与时间 $t (h)$ 的函数关系式是．（写出自变量取值范围）

查看试题解析
14. 如图，四边形ABCD是边长为 $\sqrt{5}$ cm的菱形，其中对角线BD的长为2cm，则菱形ABCD的面积为 cm² ．

查看试题解析

三、解答题（78分）

15. 若a＝ $\sqrt{3}$ +2，b＝ $\sqrt{3}$ -2，求a²b+ab²的值．

查看试题解析
16. 计算：（2 $\sqrt{3}$ +2）（2 $\sqrt{3}$ -2）+ $\sqrt{12}$ -6 $\sqrt{\frac{1}{3}}$ ．

查看试题解析
17. 解一元二次方程x²﹣4x﹣12＝0．

查看试题解析
18. 先化简再求值：当a＝ $\sqrt{5}$ 时，求a+ $\sqrt{1 - 2 a + a^{2}}$ 的值．

查看试题解析
19. 若函数y＝（2m+1）x+m+3的图象平行于直线y＝3x-3，求函数解析式．

查看试题解析
20. 《九章算术》是我国古代第一部数学专著，它的出现标志中国古代数学形成了完整的体系，“折竹抵地“问题源自《九章算术》中：“今有竹高一丈，末折抵地，去本四尺，问折者高几何？”翻译成数学问题是：如图所示，△ABC中，∠ACB＝90°，AC+AB＝10尺，BC＝4尺，求AC的长．

查看试题解析
21. 某校为了解学生参加志愿者活动的情况，随机抽取了该校八年级20名学生进行调查，统计得到这20名学生参加志愿者活动的次数如下：
3，5，3，6，3，4，4，5，2，4，5，6，1，3，5，5，4，4，2，4．
根据以上信息，得到如下不完整的频数分布表：

次数
1
2
3
4
5
6
人数
1
a
4
b
5
2

(1)、表格中的a＝， b＝．

(2)、这组数据的中位数是，众数是．

(3)、若该校八年级共有400名学生，试估计该校八年级学生参加志愿者活动的次数为3次的人数．

查看试题解析
22. 为防控“新型冠状病毒”，某药店分别用1600元、6000元购进两批防护口罩，第二批防护口罩的数量是第一批的3倍，但单价比第一批贵2元，请问药店第一批防护口罩购进了多少只？

查看试题解析
23. 图①、图②均是4×4的正方形网格，每个小正方形的边长均为1．每个小正方形的顶点叫做格点，线段AB的两个端点均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，使所画图形的顶点均在格点上，不要求写出画法．

(1)、在图①以AB为一边画一个平行四边形；

(2)、在图②以AB为对角线画一个矩形．

查看试题解析
24. 如图，在▱BFDE中，A、C分别在DE、BF的延长线上，且AE＝CF．求证：四边形ABCD是平行四边形．

查看试题解析
25. 小明和小红分别从甲、乙两地沿同一条路同时出发，相向而行．小明从甲地到乙地，小红从乙地到甲地，小明和小红离甲地的距离y（千米）与时间x（小时）之间的函数图象如图所示，根据图中提供的信息，解答下列问题：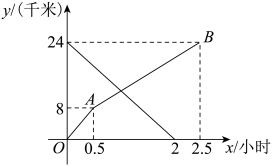

(1)、小红出发后速度为千米/小时．

(2)、求线段AB对应的函数表达式，写出自变量x的取值范围．

(3)、当小红到达甲地时，小明距乙地还有多远？

查看试题解析
26. 阅读理解：
在平面直角坐标系中，点P的坐标为（x₁ ， y₁），点Q的坐标为（x₂ ， y₂），且x₁≠x₂ ， y₁≠y₂ ，若P、Q为某矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为P、Q的“相关矩形”．如图①中的矩形为点P、Q的“相关矩形”

(1)、已知点A的坐标为（0，1）．
①若点B的坐标为（3，5），则点A、B的“相关矩形”的周长为 ▲ ．
②若点C在直线y＝5上．且点A、C的“相关矩形”为正方形，求直线AC的解析式．

(2)、已知点M的坐标为（-2，4），点N的坐标为（-5，3），若使函数 $y = \frac{k}{x}$ 的图象与点M、N的“相关矩形”有两个公共点，直接写出k的取值范围．

查看试题解析

次数	1	2	3	4	5	6
人数	1	a	4	b	5	2