吉林省松原市前郭县三校名校调研2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-07-20 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 函数 $y = \frac{1}{x - 5}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \neq 5$ B、 $x = 5$ C、 $x > 5$ D、 $x < 5$

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{12}$ C、 $\sqrt{11}$ D、 $\sqrt{36}$

查看试题解析
3. 某市一周空气质量报告中，某项污染指数的数据如下，32，35，32，33，30，32，31，则这组数据的众数是（）

A、31 B、31.5 C、32 D、34

查看试题解析
4. 如图，数轴上点 $A$ 对应的数是0，点 $B$ 对应的数是1， $B C ⊥ A B$ ，垂足为 $B$ ，且 $B C = 1$ ，以 $A$ 为圆心， $A C$ 的长为半径画弧，交数轴正半轴于点 $D$ ，则点 $D$ 表示的数为（）

A、2.2 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
5. 如图，在 $□ A B C D$ 中，以点 $B$ 为圆心，适当长为半径作弧、分别交 $B A$ 、 $B C$ 于点 $F$ 、 $G$ .再分别以点 $F$ 、 $G$ 为圆心，以大于 $\frac{1}{2} F G$ 的长为半径作弧，两弧交于点 $H$ ，作 $B H$ 交 $A D$ 于点 $E$ .若 $A B = 5$ ， $D E = 2$ ，且 $G$ 为边 $B C$ 的中点，则 $C G$ 的长为（）

A、3 B、 $\frac{7}{2}$ C、5 D、7

查看试题解析
6. 如图，在平面直角坐标系中，直线 $y = \frac{3}{4} x + 3$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 、 $B$ ，与直线 $y = - x + b$ 交于点 $C$ .若点 $C$ 的横坐标为 $- 2$ .则关于 $x$ 的不等式 $- x + b > \frac{3}{4} x + 3$ 的最大整数解为（）

A、 $- 1$ B、 $- 5$ C、 $- 3$ D、 $- 4$

查看试题解析

二、填空题（每小题3分，共24分）

7. 计算 $\sqrt{54} - \sqrt{6} =$

查看试题解析
8. 在平面直角坐标系中，一次函数 $y = - 5 x + 2023$ 的图象不经过第象限.

查看试题解析
9. 小明参加“逐梦正青春”主题演讲比赛，其演讲形象、内容、效果三项的得分分别是9分、8分、8分。若将三项得分依次按30%、40%、30%的权重确定最终成绩，则小明的最终比赛成绩为分.

查看试题解析
10. 在 $△ A B C$ 中，若 $A C = 6$ ， $B C = 8$ ，则 $A B =$ 时， $△ A B C$ 是直角三角形.

查看试题解析
11. 如图，在平面直角坐标系中，点 $A$ 、 $B$ 的坐标分别为 $(4 ， 0)$ 、 $(4 ， 4)$ .若正比例函数 $y = k x$ 与线段 $A B$ 有交点，写出一个可能的 $k$ 值为

查看试题解析
12. 如图，在正方形 $A B C D$ 中， $E$ 为 $A D$ 上一点，连接 $B E$ ，交对角线 $A C$ 于点 $F$ ，连接 $D F$ ，若 $∠ A B E = 35 °$ ，则 $∠ C F D =$ 度.

查看试题解析
13. 如图，在菱形 $A B C D$ 中， $E$ 是对角线 $A C$ 上的一点，过点 $E$ 作 $F H ∥ A D$ ， $G I ∥ A B$ ，若 $A C = 5$ ， $∠ B = 60 °$ ，则图中阴影部分图形的周长和为

查看试题解析
14. 如图，在 $△ A B C$ 中，点 $D$ 、 $E$ 分别为 $A B$ 、 $B C$ 的中点， $C F$ 平分 $∠ A C B$ ，交 $D E$ 于点 $F$ ，连接 $B F$ 并延长.交 $A C$ 于点 $G$ ，已知 $A C = 7$ ， $B F = 3$ ， $C F = 4$ ，则 $A G =$

查看试题解析

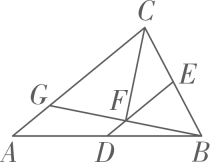
三、解答题（每小题5分，共20分）

15. 计算： $\sqrt{24} \times \sqrt{\frac{1}{6}} - {(- \sqrt{7})}^{2}$ .

查看试题解析
16. 在平面直角坐标系中，一次函数 $y = k x + 1 (k \neq 0)$ 的图象经过点 $A (1 ， 3)$

(1)、求 $k$ 的值

(2)、将这个一次函数的图象向上平移2个单位长度后得到的函数的解析式是

查看试题解析
17. 如图，池塘边有两点 $A$ 、 $B$ ，点 $C$ 是与 $B A$ 成直角的 $A C$ 方向上的一点，测得 $B C$ 的长为60米， $A C$ 的长为20米.求 $A$ 、 $B$ 两点间的距离（ $\sqrt{2} \approx 1.414$ ，结果保留小数点后一位）

查看试题解析
18. 如图，四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，其中 $A D ∥ B C$ ， $A B ∥ C D$ ， $A C = 2 O B$ ，求证：四边形 $A B C D$ 是矩形.

查看试题解析

四、解答题（每小题7分，共28分）

19. 图①，图②，图③均是5×5的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫格点，图①，图②，用③中线段 $A B$ 的点均在格点上，只用无刻度的直尺，在给定的网格中，分别按下列要求画图，并保留作图痕迹.
图① 图② 图③

(1)、在图①中以 $A B$ 为边画一个平行四边形 $A B C D$ （不是矩形），使其面积为12；

(2)、在图②中以 $A B$ 为对角线画一个菱形 $A E B F$ ，且点 $E$ 、 $F$ 在格点上；

(3)、在图③中以 $A B$ 为边画一个矩形 $A B G H$ ，使其面积为10.

查看试题解析
20. 如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度与碗的数量的关系如下表：
碗的数量（个）
2
3
4
…
高度 $(c m)$
10.2
11.4
12.6
…

(1)、若把6个这样的碗整齐地叠放在水平桌面上时，这摞碗的高度是cm；

(2)、设摞碗的数量为 $x$ （个），摞碗的高度为 $y (c m)$ ，求 $y$ 与 $x$ 之间的函数关系式；

(3)、这摞碗的高度是否可以为 $18.6 c m$ ，如果可以，求这摞碗的数量；如果不可以，请说明理由.

查看试题解析
21. 如图

(1)、【教材原题改编】改编自人教版八年级下册数学教材第51页第14题.
如图， $□ A B C D$ 的对角线 $A C$ 和 $B D$ 相交于点 $O$ ， $E F$ 过点 $O$ 且与边 $A B$ 、 $C D$ 分别相交于点 $E$ 和点 $F$ .求证： $O E = O F$ ；

(2)、【结论应用】若 $∠ A D B = 90 °$ ， $A B = 5$ ， $A D = 3$ ，则四边形 $A D F E$ 的面积为， $E F$ 的最小值为

查看试题解析
22. 为了解 $A$ 、 $B$ 两家酒店的经营状况，获得了它们去年下半年7~12月的月营业额（单位：百万元）的数据，并对数据进行整理和分析.下面给出了两条信息：① $A$ 、 $B$ 两家酒店去年7~12月月营业额的平均数、中位数、方差；② $A$ 、 $B$ 两家酒店去年7~12月月营业额折线统计图.

平均数（百万元）
中位数（百万元）
方差（百万元）
          $A$ 酒店
2.5
2.45
1.073
          $B$ 酒店
          $m$
          $n$
0.54
根据以上信息，回答下列问题：

(1)、直接写出表中 $m$ 、 $n$ 的值；

(2)、根据所得信息，你认为哪家酒店经营状况较好？请简述理由.

查看试题解析

五、解答题（每小题8分，共16分）

23. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ，对角线 $B D$ 的垂直平分线与边 $A D$ 、 $B C$ 分别相交于点M、N，连接 $B M$ 、 $D N$ .

(1)、求证：四边形 $B N D M$ 是菱形；

(2)、若四边形 $B N D M$ 的周长为52， $M N = 10$ ，求 $B D$ 的长.

查看试题解析
24. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段 $O A$ 表示货车离甲地的距离 $y$ （千米）与时间 $x$ （小时）之间的函数关系：线段 $B D$ 表示轿车离甲地的距离 $y$ （千米）与时间 $x$ （小时）之间的函数关系.点 $C$ 在线段 $B D$ 上，请根据图象解答下列问题.

(1)、轿车的速度是千米/小时；

(2)、求轿车出发后、轿车离甲地的距离 $y ($ 千米）与时间 $x$ （小时）之间的函数关系式；

(3)、在轿车行驶的过程中，轿车与货车之间的距离为20千米时，直接写出 $x$ 的值.

查看试题解析

六、解答题（每小质10分，共20分）

25. 如图
图① 图②

(1)、【操作一】如图①，在正方形 $A B C D$ 中，点 $M$ 是 $A B$ 的中点， $M N ∥ B C$ 交 $C D$ 于点 $N$ ，点 $E$ 是 $A B$ 边上的一点，连接 $C E$ ，将正方形纸片沿 $C E$ 所在直线折叠，点 $B$ 的对应点 $B^{'}$ 落在 $M N$ 上，连接 $B^{'} D$ ，求证： $△ C B^{'} D$ 是等边三角形；

(2)、【操作二】在图①的基础上继续折叠，如图②，点 $F$ 是 $C D$ 边上的一点，连接 $A F$ ，将正方形纸片沿 $A F$ 所在直线折叠，点 $D$ 的对应点 $D^{'}$ 落在 $M N$ 上，求证： $△ B C E ≌ △ D A F$ ；

(3)、【应用】在图②中，若 $A B = 2$ ，请直接写出线段 $B^{'} D^{'}$ 的长.

查看试题解析
26. 如图，在平面直角坐标系中， $O$ 为坐标原点，直线 $y = k x + 6$ 与 $x$ 轴交于点 $A (8 ， 0)$ ，与 $y$ 轴交于点 $B$ ，过点 $B$ 的直线 $B C$ 将 $△ A B O$ 的面积平分

(1)、求 $k$ 的值和点 $B$ 的坐标；

(2)、求 $△ A B C$ 的面积；

(3)、求直线 $B C$ 的解析式；

(4)、点 $D$ 是坐标平面内的点，当以 $O$ 、 $B$ 、 $C$ 、 $D$ 为顶点的四边形是平行四边形时，若该平行四边形的边所在的直线与直线 $A B$ 的交点为 $P$ （点 $P$ 不与点 $A$ 、 $B$ 重合），请直接写出点 $P$ 的坐标.

查看试题解析

	平均数（百万元）	中位数（百万元）	方差（百万元）
$A$ 酒店	2.5	2.45	1.073
$B$ 酒店	$m$	$n$	0.54

碗的数量（个）	2	3	4	…
高度 $(c m)$	10.2	11.4	12.6	…