云南省昭通市永善县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-20 类型:期末考试
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
-
1. 中华文字是中国华夏民族5000年文化积淀的艺术现宝。下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列二次根式中能与合并的二次根式是( )A、 B、 C、 D、3. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
2. 下列二次根式中能与合并的二次根式是( )A、 B、 C、 D、3. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
 A、AB∥CD,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC4. 如图,在△ABC中,AC的垂直平分线交AB于点DCDC平分∠ACB,若 , 则∠B的度数为( )
A、AB∥CD,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC4. 如图,在△ABC中,AC的垂直平分线交AB于点DCDC平分∠ACB,若 , 则∠B的度数为( )
 A、 B、 C、35° D、5. 某射击运动员在训练中射击了10次,成绩如图所示:下列结论正确的是( )
A、 B、 C、35° D、5. 某射击运动员在训练中射击了10次,成绩如图所示:下列结论正确的是( )
 A、众数是8,中位数是8 B、众数是8,中位数是8.5 C、平均数是8.2,方差是1.2 D、平均数是8.方差是1.26. 如果点E、F、G、H分别是菱形ABCD四边AB、BC、CD、DA上的中点,那么四边形EFGH是( )A、菱形 B、矩形 C、正方形 D、平行四边形7. 直线 的图象如图所示,则函数 的图象大致是( )
A、众数是8,中位数是8 B、众数是8,中位数是8.5 C、平均数是8.2,方差是1.2 D、平均数是8.方差是1.26. 如果点E、F、G、H分别是菱形ABCD四边AB、BC、CD、DA上的中点,那么四边形EFGH是( )A、菱形 B、矩形 C、正方形 D、平行四边形7. 直线 的图象如图所示,则函数 的图象大致是( ) A、
A、 B、
B、 C、
C、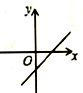 D、
D、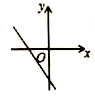 8. 如图,在平行四边形ABCD中,AB⊥AC,若AB=8,AC=12,则BD的长是( )
8. 如图,在平行四边形ABCD中,AB⊥AC,若AB=8,AC=12,则BD的长是( )
 A、22 B、16 C、18C D、209. 如图,矩形ABCD中,E、F、M为AB、BC、CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为( )
A、22 B、16 C、18C D、209. 如图,矩形ABCD中,E、F、M为AB、BC、CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为( ) A、5 B、5 C、6 D、610. 如图,一次函数与的图象相,交于点P(m,4),则关于x、y的二元一次方程组的解是( )
A、5 B、5 C、6 D、610. 如图,一次函数与的图象相,交于点P(m,4),则关于x、y的二元一次方程组的解是( )
 A、 B、 C、 D11. 计算: , …归纳各计算结果中的个位数字规律,猜测的个位数字是( )A、1 B、3 C、7 D、512. 如图,分别以B△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE、AB相交于点G,若 , 下列结论:
A、 B、 C、 D11. 计算: , …归纳各计算结果中的个位数字规律,猜测的个位数字是( )A、1 B、3 C、7 D、512. 如图,分别以B△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE、AB相交于点G,若 , 下列结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA。
其中正确结论的个数有( )
A、1 B、2 C、3 D、4二、填空题(本大题共4小题,每小题2分,共8分)
-
13. 函数 的自变量x的取值范围是.14. 分解因式: = .15. 已知整数a使得不等式组的解集为 , 且使得一次函数的图象不经过第四象限,则整数a的值为。16. 如下图,在△ABC中,AB=AC,BC=6,△ABC面积为12,AD⊥BC于点D,直线EF垂直平分AB交AB于点E,交BC于点F,P为直线EF上一动点,则△PBD的周长的最小值为。

三、解答题(本大题共8小题,共56分)
-
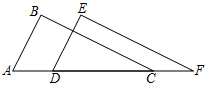
17. 计算:。18. 如图,点A,D,C,F在同一条直线上,AD=CF,AB=DE,AB∥DE.求证:BC=EF.
 19. 在△ABC中, , , , , , 求△ABC的面积。20. 如图,在平面直角坐标系中,A(3,4),B(1,2),C(5,1)。
19. 在△ABC中, , , , , , 求△ABC的面积。20. 如图,在平面直角坐标系中,A(3,4),B(1,2),C(5,1)。 (1)、在图中作出△ABC关于y轴的对称图形;(2)、写出点、、的坐标(直接写答案)
(1)、在图中作出△ABC关于y轴的对称图形;(2)、写出点、、的坐标(直接写答案): , :;:。
(3)、求△ABC的面积。21. 2023年6月26日是“国际禁毒日”,某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动.为了解竞赛情况,从两个年级各随机抽取了10名同学的成绩(满分为100分),收集数据为:七年级90,95,95,80,90,80,85,90,85,100;
八年级85,85,95,80,95,90,90,90,100,90。
整理数据:

80
85
90
95
100
七年级
2
2
3
2
1
八年级
1
2
4
a
1
分析数据:
平均数
中位数
众数
方差
七年级
89
b
90
39
八年级
c
90
d
300
根据以上信息回答下列问题:
(1)、请直接写出表格中a,b,c,d的值;(2)、通过数据分析,你认为哪个年级的成绩比较好?请说明理由;(3)、该校七、八年级共有600人,本次竞赛成绩不低于90分的为“优秀”。估计这两个年级共有多少名学生达到“优秀”?22. 如图,已知四边形ABCD是平行四边形,并且。
 (1)、求证:四边形ABCD为矩形;(2)、点E是AB边的中点,F为AD边上一点. , 若CE=4,CF=5,求DF的长。23. 某商场准备购进A、B两种书包,每个A种书包比B种书包的进价少20元,用700元购进A种书包的个数是用450元购进B种书包个数的2倍,A种书包每个标价是90元,B种书包每个标价是130元。请解答下列问题:(1)、A、B两种书包每个进价各是多少元?(2)、若该商场购进B种书包的个数比A种书包的2倍还多5个,且A种书包不少于18个,购进A、B两种书包的总费用不超过5450元,则该商场有哪几种进货方案?(3)、该商场按(2)中获利最大的方案购进书包,在销售前,拿出5个书包赠送给某希望小学,剩余的书包全部售出,其中两种书包共有4个样品,每种样品都打五折,商场仍获利1370元。请直接写出赠送的书包和样品中,B种书包各有几个?24. 如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程组的解,点C是直线与直线AB的交点,点D在线段OC上,。
(1)、求证:四边形ABCD为矩形;(2)、点E是AB边的中点,F为AD边上一点. , 若CE=4,CF=5,求DF的长。23. 某商场准备购进A、B两种书包,每个A种书包比B种书包的进价少20元,用700元购进A种书包的个数是用450元购进B种书包个数的2倍,A种书包每个标价是90元,B种书包每个标价是130元。请解答下列问题:(1)、A、B两种书包每个进价各是多少元?(2)、若该商场购进B种书包的个数比A种书包的2倍还多5个,且A种书包不少于18个,购进A、B两种书包的总费用不超过5450元,则该商场有哪几种进货方案?(3)、该商场按(2)中获利最大的方案购进书包,在销售前,拿出5个书包赠送给某希望小学,剩余的书包全部售出,其中两种书包共有4个样品,每种样品都打五折,商场仍获利1370元。请直接写出赠送的书包和样品中,B种书包各有几个?24. 如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程组的解,点C是直线与直线AB的交点,点D在线段OC上,。
 (1)、求点C的坐标;(2)、求直线AD的解析式;(3)、P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若在(在,请写出点Q的坐标:若不存在,请说明理由。
(1)、求点C的坐标;(2)、求直线AD的解析式;(3)、P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若在(在,请写出点Q的坐标:若不存在,请说明理由。