广东省潮州市湘桥区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-19 类型:期末考试
一、选择题(每小题3分,共30分,)
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 某班有7个学习小组,每组的人数分别为3,4,5,6,6,7,7这组数据的中位数是( )A、4 B、5 C、5.5 D、63. 以下列长度的线段为边,不能构成直角三角形的是( )A、2、3、4 B、1、1、 C、3、4、5 D、5、12、134. 下列计算正确的是( )A、 B、 C、 D、5. 如图,四边形是平行四边形,点在线段的延长线上,若 , 则的度数为( )
 A、100° B、110° C、120° D、130°6. 甲、乙、丙、丁四人进行射箭测试,每人测试10次,射箭成绩的平均数都是8.8环,方差分别为 , , , , 则射箭成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁7. 直线与轴的交点是 , 则的值是( )A、3 B、2 C、-2 D、-38. 如图,在矩形中, , 则的长为( )
A、100° B、110° C、120° D、130°6. 甲、乙、丙、丁四人进行射箭测试,每人测试10次,射箭成绩的平均数都是8.8环,方差分别为 , , , , 则射箭成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁7. 直线与轴的交点是 , 则的值是( )A、3 B、2 C、-2 D、-38. 如图,在矩形中, , 则的长为( ) A、 B、8 C、 D、49. 已知一次函数的函数值随的增大而减小,则该函数的图象大致是( )A、
A、 B、8 C、 D、49. 已知一次函数的函数值随的增大而减小,则该函数的图象大致是( )A、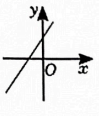 B、
B、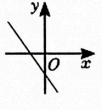 C、
C、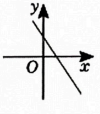 D、
D、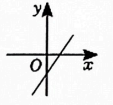 10. 如图,正方形的边长为 , 为上一点,连接 , 于点 , 连接 , 且 , 若 , 则的面积为( )
10. 如图,正方形的边长为 , 为上一点,连接 , 于点 , 连接 , 且 , 若 , 则的面积为( ) A、8 B、6 C、4 D、
A、8 B、6 C、4 D、二、填空题(每小题4分,共28分,请把正确的答案写在横线上)
-
11. 计算: = .12. 已知一组数据3、x、4、5、6的众数是6,则x的值是 .13. 如图,在平行四边形中, , 点分别是的中点,则.
 14. 如图,在中, , 点是边的中点, , 则的长为.
14. 如图,在中, , 点是边的中点, , 则的长为. 15. 如图,直线与相交于点 , 点的横坐标为-1,则关于的不等式的解集为.
15. 如图,直线与相交于点 , 点的横坐标为-1,则关于的不等式的解集为. 16. 湘桥区某中学举行主题为“青春心向党”的党史知识竞赛,小明同学参加本次知识竞赛,他获得笔试成绩得分98分,抢答成绩得分90分,演讲成绩得分95分,若依次按50%、10%、40%的比例来确定总成绩,则小明同学党史知识竞赛总成绩是分.17. 如图,在四边形中, , , 对角线交于点 , 平分 , 过点作交的延长线于点 , 连接 , , , 则的长为.
16. 湘桥区某中学举行主题为“青春心向党”的党史知识竞赛,小明同学参加本次知识竞赛,他获得笔试成绩得分98分,抢答成绩得分90分,演讲成绩得分95分,若依次按50%、10%、40%的比例来确定总成绩,则小明同学党史知识竞赛总成绩是分.17. 如图,在四边形中, , , 对角线交于点 , 平分 , 过点作交的延长线于点 , 连接 , , , 则的长为.
三、解答题(共3小题,共24分)
-
18. 计算:(1)、(2)、.19. 如图,已知 , , , 请问是直角三角形吗?请说出你的理由.
 20. 如图,在平行四边形中,点分别在上,且.
20. 如图,在平行四边形中,点分别在上,且.求证:四边形是平行四边形.

四、解答题(共2小题,共18分)
-
21. 如图矩形沿着对角线翻折,点落在点处,与相交于点 , 若.
 (1)、求证:;(2)、求的长.22. 潮州市湘桥区农投公司现有22吨优质农产品需要销售,经市场调查,采用批发、零售两种销售方式,这两种销售方式每天的销量及每顿所获得利润如表:
(1)、求证:;(2)、求的长.22. 潮州市湘桥区农投公司现有22吨优质农产品需要销售,经市场调查,采用批发、零售两种销售方式,这两种销售方式每天的销量及每顿所获得利润如表:销售方式
批发
零售
利润(元/吨)
1200
2000
假设农投公司售完22吨优质农产品,共批发了吨,所获总利润为元.
(1)、求出与之间的函数关系式;(2)、如果农投公司销售这批优质农产品共获利28000元,请计算农投公司通过批发方式销售这批农产品共多少吨?五、解答题(共2小题,共20分)

