湖北省孝感市云梦县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-07-19 类型:期末考试
一、精心选一选(本大题共8小题,每小题3分,满分24分,在每小题给出的四个选项中只有一个正确选项,请在答题卡上把正确答案的代号涂黑)
-
1. 下列各数中,有理数是( )A、 B、 C、3.1415 D、2. 下图是一个不等式组中的所有不等式的解集在数轴上的表示,则该不等式组的解集是( )
 A、 B、 C、 D、无解3. 估计的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间4. 下列调查中,调查方式选择合理的是( )A、为了调查孝感市中小学生的防火意识,选择全面调查 B、为了了解黄香小学某班学生新冠病毒疫苗接种情况,选择抽样调查 C、为了了解云梦县人均收入情况,选择全面调查 D、为了了解一批袋装食品是否含有防腐剂,选择抽样调查5. 下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图,在中, , , , 两点分别在边 , 上,平分 , .图中的等腰三角形共有( )
A、 B、 C、 D、无解3. 估计的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间4. 下列调查中,调查方式选择合理的是( )A、为了调查孝感市中小学生的防火意识,选择全面调查 B、为了了解黄香小学某班学生新冠病毒疫苗接种情况,选择抽样调查 C、为了了解云梦县人均收入情况,选择全面调查 D、为了了解一批袋装食品是否含有防腐剂,选择抽样调查5. 下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图,在中, , , , 两点分别在边 , 上,平分 , .图中的等腰三角形共有( ) A、2个 B、3个 C、4个 D、5个7. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有人,辆车,可列方程组为( )A、 B、 C、 D、8. 已知点与点关于轴对称,则在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、2个 B、3个 C、4个 D、5个7. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有人,辆车,可列方程组为( )A、 B、 C、 D、8. 已知点与点关于轴对称,则在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、细心填一填(本大题共8小题,每小题3分,满分24分.请把答案填在答题卡相应题号的横线上)
-
9. 0.008的立方根是.10. 某中学为了了解2000名学生的视力情况,从中抽取了200名学生进行检测.则这个抽样调查的样本容量是.11. 将先向上平移7个单位长度,再向左平移8个单位长度,得到点 , 则点的坐标是.12. 如图,将直角三角板与直尺贴在一起,使三角板的直角顶点()在直尺的一边上,若 , 则的度数等于.
 13. 关于、的方程组的解与满足条件 , 则的最大整数值是.14. 某种商品的进价为1000元,出售时标价为1500元,由于该商品积压,商店决定打折出售,但要保证利润率不低于20%,则至多可打折.15. 如图,直线经过点 , 为坐标原点,为线段上一动点,若 , , , 则长度的最小值为.
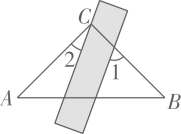
13. 关于、的方程组的解与满足条件 , 则的最大整数值是.14. 某种商品的进价为1000元,出售时标价为1500元,由于该商品积压,商店决定打折出售,但要保证利润率不低于20%,则至多可打折.15. 如图,直线经过点 , 为坐标原点,为线段上一动点,若 , , , 则长度的最小值为. 16. 如图,已知平分 , 平分 , 、与直线分别交于点、 , , 下列结论:①;②);③;④若 , 则.其中正确的是.(填写所有正确结论的序号)
16. 如图,已知平分 , 平分 , 、与直线分别交于点、 , , 下列结论:①;②);③;④若 , 则.其中正确的是.(填写所有正确结论的序号)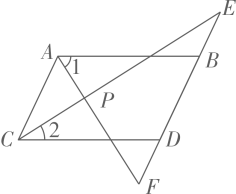
三、专心解一解(本大题共8小题,满分72分,请认真读题,冷静思考,解答题应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答题卡相应题号的位置)
-
17. 计算: .18. 解方程组:(1)、(2)、19. 解不等式组 , 并把不等式组的解集表示在数轴上.20. 云梦县中百超市为了解消费者支付方式的情况,随机抽取了名消费者进行调查,消费者的支付方式分为以下四种情况:微信、支付宝、现金、其他。该超市将调查结果绘制成如下两幅统计图.

根据统计图提供的信息解答下列问题:
(1)、的值为;(2)、求扇形统计图中“现金”所在扇形的圆心角度数;(3)、根据以上信息补全条形统计图;(4)、如果某天共有560名消费者去云梦中百超市购物,估计其中使用微信或者支付宝进行支付的约有多少人?21. 已知:如图, , . (1)、求证:.(2)、若 , , 求证:.22. 六月份,某电器商店用4200元购进20台型和10台型电风扇,分别以200元/台和160元/台的价格进行销售,全部售完后,型电风扇的总利润比型电风扇的总利润多600元.(利润=销售收入-进货成本,全年进价、售价均保持不变)(1)、求每台型电风扇和每台型电风扇的进价分别是多少元?(2)、为满足市场需求,七月份该电器商店决定再用不超过6750元的资金采购型和型电风扇共50台,且型电风扇的数量不少于23台,问电器商店有哪几种进货方案?(3)、在(2)的条件下,请你通过计算判断,电器商店销售完这50台电风扇能否实现获利2300元的目标?若能,请给出相应的进货方案;若不能,请说明理由.23. 在一次数学活动课上,同学们用一个含有60°角的直角三角板和两条平行线展开探究.如图,在中, , , .
(1)、求证:.(2)、若 , , 求证:.22. 六月份,某电器商店用4200元购进20台型和10台型电风扇,分别以200元/台和160元/台的价格进行销售,全部售完后,型电风扇的总利润比型电风扇的总利润多600元.(利润=销售收入-进货成本,全年进价、售价均保持不变)(1)、求每台型电风扇和每台型电风扇的进价分别是多少元?(2)、为满足市场需求,七月份该电器商店决定再用不超过6750元的资金采购型和型电风扇共50台,且型电风扇的数量不少于23台,问电器商店有哪几种进货方案?(3)、在(2)的条件下,请你通过计算判断,电器商店销售完这50台电风扇能否实现获利2300元的目标?若能,请给出相应的进货方案;若不能,请说明理由.23. 在一次数学活动课上,同学们用一个含有60°角的直角三角板和两条平行线展开探究.如图,在中, , , . (1)、如图1,点在上,点在上,与交于点 , 若 , 求的度数;(2)、如图2,点在上,点在上方,点在下方,与交于点 , 作的角平分线并反向延长与的角平分线交于点 , 求的度数;(3)、如图3,点在上,点在直线 , 之间(不含在 , 上),点在下方, , 分别与交于点 , .设 , 是否存在正整数和 , 使得.若存在,请求出和的值;若不存在,请说明理由.24. 如图,在平面直角坐标系中,已知点 , , , 其中 , 满足.
(1)、如图1,点在上,点在上,与交于点 , 若 , 求的度数;(2)、如图2,点在上,点在上方,点在下方,与交于点 , 作的角平分线并反向延长与的角平分线交于点 , 求的度数;(3)、如图3,点在上,点在直线 , 之间(不含在 , 上),点在下方, , 分别与交于点 , .设 , 是否存在正整数和 , 使得.若存在,请求出和的值;若不存在,请说明理由.24. 如图,在平面直角坐标系中,已知点 , , , 其中 , 满足. (1)、求 , 两点的坐标;(2)、如图1,是直线上一点,求出 , 之间满足的关系式;(3)、如图2,过点作直线 , 已知是直线上的一点,
(1)、求 , 两点的坐标;(2)、如图1,是直线上一点,求出 , 之间满足的关系式;(3)、如图2,过点作直线 , 已知是直线上的一点,①求出 , 之间满足的关系式;
②若 , 求的取值范围.