湖北省随州市曾都区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-19 类型:期末考试
一、选择题(本题共10小题,每小题3分,共30分.每小题给出的四个选项中只有一项是符合题目要求的)
-
1. 要使二次根式有意义,的取值范围是( )A、 B、 C、 D、2. 已知正比例函数 , 若随的增大而减小,则的取值范围是( )A、 B、 C、 D、3. 如图,一竖直的大树在离地面3米处折断,树的顶端落在地面离大树底端4米处,大树折断之前的高度为( )
 A、7米 B、8米 C、9米 D、12米4. 下列二次根式中,化简后能与进行合并的是( )A、 B、 C、 D、5. 在四边形中,对角线与交于点 , 下列条件不能判定四边形是平行四边形的是( )A、 , B、 , C、 , D、 ,6. 小明所在班级10名同学的身高(単位:cm)数据如下:165,158,168,162,174,168,162,165,168,170.下列统计量中,能够描述这组数据离散程度的是( )A、平均数 B、方差 C、众数 D、中位数7. 在矩形中,对角线与交于点 , 下列结论一定正确的是( )A、是等边三角形 B、 C、 D、平分8. 关于函数的图象与性质,下列说法正确的是( )A、函数图象经过第一、二、三象限 B、函数图象与轴交点坐标为 C、图象是与平行的一条直线 D、当时,函数值有最小值39. 在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦.古希腊哲学家柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17…若此类勾股数的勾为( , m为正整数),则其弦(结果用含的式子表示)是( )A、 B、 C、 D、10. 甲、乙两辆汽车从地出发,均匀速向地行驶,当某辆汽车到达B地时,该汽车就停止行驶.甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距 , 甲行驶的时间为与的关系如图所示,下列结论:①甲车行驶的速度是;②乙出发后追上甲;③A,B两地相距;④甲比乙晚到 . 其中正确结论的个数是( )
A、7米 B、8米 C、9米 D、12米4. 下列二次根式中,化简后能与进行合并的是( )A、 B、 C、 D、5. 在四边形中,对角线与交于点 , 下列条件不能判定四边形是平行四边形的是( )A、 , B、 , C、 , D、 ,6. 小明所在班级10名同学的身高(単位:cm)数据如下:165,158,168,162,174,168,162,165,168,170.下列统计量中,能够描述这组数据离散程度的是( )A、平均数 B、方差 C、众数 D、中位数7. 在矩形中,对角线与交于点 , 下列结论一定正确的是( )A、是等边三角形 B、 C、 D、平分8. 关于函数的图象与性质,下列说法正确的是( )A、函数图象经过第一、二、三象限 B、函数图象与轴交点坐标为 C、图象是与平行的一条直线 D、当时,函数值有最小值39. 在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦.古希腊哲学家柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17…若此类勾股数的勾为( , m为正整数),则其弦(结果用含的式子表示)是( )A、 B、 C、 D、10. 甲、乙两辆汽车从地出发,均匀速向地行驶,当某辆汽车到达B地时,该汽车就停止行驶.甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距 , 甲行驶的时间为与的关系如图所示,下列结论:①甲车行驶的速度是;②乙出发后追上甲;③A,B两地相距;④甲比乙晚到 . 其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每小题3分,共18分.把正确答案填在答题卡对应题号的横线上)
-
11. 化简: , , .12. 如图,在菱形中, , 对角线 , 相交于点 , 为的中点,则的度数为 .
 13. 已知 , 则代数式的值为 .14. 4月23日是“世界读书日”.某中学为了了解八年级学生读书情况,随机调查了50名学生的读书数量,统计数据如表所示:
13. 已知 , 则代数式的值为 .14. 4月23日是“世界读书日”.某中学为了了解八年级学生读书情况,随机调查了50名学生的读书数量,统计数据如表所示:数量/册 0
1
2
3
4
人数
3
13
16
17
1
若将这50名学生读书册数的众数记为 , 中位数记为 , 则 .
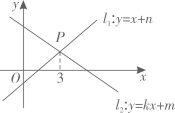
15. 如图,直线与直线交于点 , 下列结论:① , ;②关于的方程的解为;③关于的不等式的解集为;
④直线上有两点 , , 若时,则 . 其中正确结论的序号是 .
 16. 如图,在正方形中,E,F分别在边 , 上,且 , 将沿翻折,使点落在正方形内一点 , 的平分线交于点 , 连接 , 若 , 则的度数为 , 点到直线的距离为 .
16. 如图,在正方形中,E,F分别在边 , 上,且 , 将沿翻折,使点落在正方形内一点 , 的平分线交于点 , 连接 , 若 , 则的度数为 , 点到直线的距离为 .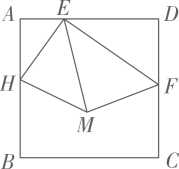
三、解答题(本题共8小题,共72分.解答应写出必要的演算步㻓、文字说明或证明过程)
-
17. 计算:(1)、;(2)、 .18. 已知中, , , 所对边长分别为 .(1)、若 , , , 求;(2)、若三边满足 , 试判断的形状.19. 如图,在平行四边形中 .
 (1)、在边AD上找一点E,连接BE,使得BE平分 . (尺规作图,不写作法,但保留作图痕迹)(2)、在(1)的条件下,在边BC上取一点F,使得 , 连接EF,请判断四边形的形状,并说明理由.20. 观察下列等式及验证,解答后面的问题:
(1)、在边AD上找一点E,连接BE,使得BE平分 . (尺规作图,不写作法,但保留作图痕迹)(2)、在(1)的条件下,在边BC上取一点F,使得 , 连接EF,请判断四边形的形状,并说明理由.20. 观察下列等式及验证,解答后面的问题:第1个等式: , 验证:;
第2个等式: , 验证:;
第3个等式: , 验证: .
(1)、请写出第4个等式,并验证;(2)、按照以上各等式反映的规律,猜想第个为正整数,且等式,并通过计算验证你的猜想.21. 五月份,教育部等七部门联合印发了《全面加强和改进新时代学生心理健康工作专项行动计划》.某校组织八年级学生开展了一次心理健康知识竞赛,现从中随机抽取10名男生和10名女生的竞赛成绩(百分制),进行整理、描述和分析,成绩得分用表示(为整数),共分成四组:A.;B.;C.;D. .10名男生的成绩在组中的数据是:90,92,94.
10名女生的成绩是:96,83,96,88,99,96,90,100,89,83.
抽取的10名男生成绩扇形统计图

抽取的男、女生各10名成绩统计表
性别 平均数 中位数 众数 方差 男生 92 a 99 34.1 34.1 女生 92 93 b 35.2 35.2 根据以上信息,解答下列问题:
(1)、直接写出图表中的值: , , ;(2)、你认为在此次竞赛中,是男生的成绩更好些,还是女生的成绩更好些?请说明理由(写出一条即可).(3)、若该校八年级共有600人,其中男生占 , 试估计八年级学生中,成绩在90分(不含90分)以上的男生有多少人?22. 已知正方形 , 为对角线上一点. (1)、如图1,连接 , , 求证:;(2)、如图2,F是延长线上一点, , 交于点 , 判断的形状,并说明理由;(3)、在(2)的条件下,若 , , 连接 , 直接写出的长为 .23. 某商场计划购进甲、乙两种商品共80件进行销售,已知甲种商品的进价为120元/件,乙种商品的进价为80元/件,甲种商品的销售单价为150元/件,乙种商品的销售单价(元/件)与购进乙种商品的数量(件)之间的函数关系如图所示.
(1)、如图1,连接 , , 求证:;(2)、如图2,F是延长线上一点, , 交于点 , 判断的形状,并说明理由;(3)、在(2)的条件下,若 , , 连接 , 直接写出的长为 .23. 某商场计划购进甲、乙两种商品共80件进行销售,已知甲种商品的进价为120元/件,乙种商品的进价为80元/件,甲种商品的销售单价为150元/件,乙种商品的销售单价(元/件)与购进乙种商品的数量(件)之间的函数关系如图所示. (1)、求(元/件)关于(件)的函数关系式(不要求写出自变量的取值范围);(2)、当购进乙种商品30件时,求销售完80件甲、乙两种商品获得的总利润;(3)、实际经营时,因原材料价格上张,甲、乙两种商品的进价均提高了 , 为保证销售完后总利润不变,商场决定将这两种商品的销售单价均提高元,且不超过乙种商品原销售单价的 , 求的最大值.24. 已知矩形的边 , 在坐标轴上,点 , 直线分别交线段及轴、轴于点 .
(1)、求(元/件)关于(件)的函数关系式(不要求写出自变量的取值范围);(2)、当购进乙种商品30件时,求销售完80件甲、乙两种商品获得的总利润;(3)、实际经营时,因原材料价格上张,甲、乙两种商品的进价均提高了 , 为保证销售完后总利润不变,商场决定将这两种商品的销售单价均提高元,且不超过乙种商品原销售单价的 , 求的最大值.24. 已知矩形的边 , 在坐标轴上,点 , 直线分别交线段及轴、轴于点 . (1)、直接写出点D,E,F的坐标;(2)、如图1,为线段DF(不包括端点)上一动点,连接 , 设点的横坐标为 , 的面积为 , 求关于的函数关系式,并写出自变量的取值范围;(3)、如图2,是线段上一动点,点在第一象限,且在直线上,若是以为直角边的等腰直角三角形,请直接写出点的坐标.
(1)、直接写出点D,E,F的坐标;(2)、如图1,为线段DF(不包括端点)上一动点,连接 , 设点的横坐标为 , 的面积为 , 求关于的函数关系式,并写出自变量的取值范围;(3)、如图2,是线段上一动点,点在第一象限,且在直线上,若是以为直角边的等腰直角三角形,请直接写出点的坐标.