2023年中考数学真题分类汇编（全国版）：代数式

试卷更新日期：2023-07-19 类型：二轮复习

进入出卷网下载

一、选择题

1. 对于实数a，b定义运算“⊗”为 $a \otimes b = b^{2} - a b$ ，例如 $3 \otimes 2 = 2^{2} - 3 \times 2 = - 2$ ，则关于x的方程 $(k - 3)$ $\otimes x = k - 1$ 的根的情况，下列说法正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
2. 已知一列均不为1的数 $a_{1} ， a_{2} ， a_{3} ， ⋯ ， a_{n}$ 满足如下关系： $a_{2} = \frac{1 + a_{1}}{1 - a_{1}} ， a_{3} = \frac{1 + a_{2}}{1 - a_{2}}$ ， $a_{4} = \frac{1 + a_{3}}{1 - a_{3}} ， ⋯ ， a_{n + 1} = \frac{1 + a_{n}}{1 - a_{n}}$ ，若 $a_{1} = 2$ ，则 $a_{2023}$ 的值是（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{3}$ C、 $- 3$ D、2

查看试题解析
3. 若 $a^{2} + 3 a - 4 = 0$ ，则 $2 a^{2} + 6 a - 3 =$ （）

A、5 B、1 C、 $- 1$ D、0

查看试题解析
4. 观察下边的数表（横排为行，竖排为列），按数表中的规律，分数 $\frac{20}{2023}$ 若排在第a行b列，则 $a - b$ 的值为（）
      $\frac{1}{1}$
      $\frac{1}{2}$      $\frac{2}{1}$
      $\frac{1}{3}$      $\frac{2}{2}$      $\frac{3}{1}$
      $\frac{1}{4}$      $\frac{2}{3}$      $\frac{3}{2}$     $\frac{4}{1}$
……

A、2003 B、2004 C、2022 D、2023

查看试题解析
5. 用长度相同的木棍按如图所示的规律拼图案，其中第①个图案用了9根木棍，第②个图案用了14根木棍，第③个图案用了19根木棍，第④个图案用了24根木棍，……，按此规律排列下去，则第⑧个图案用的木棍根数是（）

A、39 B、44 C、49 D、54

查看试题解析
6. 用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）

A、14 B、20 C、23 D、26

查看试题解析
7. 对于正数x，规定 $f (x) = \frac{2 x}{x + 1}$ ，例如： $f (2) = \frac{2 \times 2}{2 + 1} = \frac{4}{3}$ ， $f (\frac{1}{2}) = \frac{2 \times \frac{1}{2}}{\frac{1}{2} + 1} = \frac{2}{3}$ ， $f (3) = \frac{2 \times 3}{3 + 1} = \frac{3}{2}$ ， $f (\frac{1}{3}) = \frac{2 \times \frac{1}{3}}{\frac{1}{3} + 1} = \frac{1}{2}$ ，计算： $f (\frac{1}{101}) + f (\frac{1}{100}) + f (\frac{1}{99}) + ⋯ + f (\frac{1}{3}) + f (\frac{1}{2}) + f (1) +$ $f (2) + f (3) + ⋯ + f (99) + f (100) + f (101) =$ （　　）

A、199 B、200 C、201 D、202

查看试题解析
8. 如图，四边形 $A B C D$ 是边长为 $\frac{1}{2}$ 的正方形，曲线 $D A_{1} B_{1} C_{1} D_{1} A_{2} ⋯$ 是由多段 $90 °$ 的圆心角的圆心为 $C$ ，半径为 $C B_{1}$ ； $\overset{⌢}{C_{1} D_{1}}$ 的圆心为 $D$ ，半径为 $D C_{1} ⋯ ， \overset{⌢}{D A_{1}} 、 \overset{⌢}{A_{1} B_{1}} 、 \overset{⌢}{B_{1} C_{1}} 、 \overset{⌢}{C_{1} D_{1}} ⋯$ 的圆心依次为 $A 、 B 、 C 、 D$ 循环，则 $\overset{⏜}{A_{2023} B_{2023}}$ 的长是（）

A、 $\frac{4045 π}{2}$ B、 $2023 π$ C、 $\frac{2023 π}{4}$ D、 $2022 π$

查看试题解析
9. 在多项式 $x - y - z - m - n$ （其中 $x > y > z > m > n$ ）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如： $x - y - | z - m | - n = x - y - z + m - n$ ， $| x - y | - z - | m - n | = x - y - z - m + n$ ， ……．
下列说法：

①存在“绝对操作”，使其运算结果与原多项式相等；

②不存在“绝对操作”，使其运算结果与原多项式之和为 $0$ ；

③所有的“绝对操作”共有 $7$ 种不同运算结果．

其中正确的个数是（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析

二、填空题

10. 定义新运算： $(a ， b) \cdot (c ， d) = a c + b d$ ，其中 $a$ ， $b$ ， $c$ ， $d$ 为实数．例如： $(1 ， 2) \cdot (3 ， 4) = 1 \times 3 + 2 \times 4 = 11$ ．如果 $(2 x ， 3) \cdot (3 ， - 1) = 3$ ，那么 $x =$ ．

查看试题解析
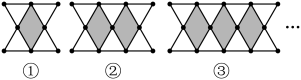
11. 已知实数 $m$ 满足 $m^{2} - m - 1 = 0$ ，则 $2 m^{3} - 3 m^{2} - m + 9 =$ ．

查看试题解析
12. 某校计划给每个年级配发n套劳动工具，则3个年级共需配发套劳动工具．

查看试题解析
13. 若 $x + y = 3$ ， $x y = 2$ ，则 $x^{2} y + x y^{2}$ 的值是．

查看试题解析
14. 用火柴棍拼成如下图案，其中第①个图案由4个小等边三角形围成1个小菱形，第②个图案由6个小等边三角形围成2个小菱形，……，若按此规律拼下去，则第n个图案需要火柴棍的根数为（用含n的式子表示）．

查看试题解析
15. 某天老师给同学们出了一道趣味数学题：
设有编号为1-100的100盏灯，分别对应着编号为1-100的100个开关，灯分为“亮”和“不亮”两种状态，每按一次开关改变一次相对应编号的灯的状态，所有灯的初始状态为“不亮”．现有100个人，第1个人把所有编号是1的整数倍的开关按一次，第2个人把所有编号是2的整数倍的开关按一次，第3个人把所有编号是3的整数倍的开关按一次，……，第100个人把所有编号是100的整数倍的开关按一次．问最终状态为“亮”

的灯共有多少盏？

几位同学对该问题展开了讨论：

甲：应分析每个开关被按的次数找出规律：

乙：1号开关只被第1个人按了1次，2号开关被第1个人和第2个人共按了2次，3号开关被第1个人和第3个人共按了2次，……

丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态．

根据以上同学的思维过程，可以得出最终状态为“亮”的灯共有盏．

查看试题解析
16. 若 $x = 3$ 是关x的方程 $a x^{2} - b x = 6$ 的解，则 $2023 - 6 a + 2 b$ 的值为．

查看试题解析
17. 定义一种新运算：对于两个非零实数 $a 、 b$ ， $a ※ b = \frac{x}{a} + \frac{y}{b}$ ．若 $2 ※ (- 2) = 1$ ，则 $(- 3) ※ 3$ 的值是．

查看试题解析
18. 烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护．通常用碳原子的个数命名为甲烷、乙烷、丙烷、……、癸烷（当碳原子数目超过 $10$ 个时即用汉文数字表示，如十一烷、十二烷……）等，甲烷的化学式为 $C H_{4}$ ，乙烷的化学式为 $C_{2} H_{6}$ ，丙烷的化学式为 $C_{3} H_{8}$ ……，其分子结构模型如图所示，按照此规律，十二烷的化学式为．

查看试题解析
19. 已知 $x^{2} - 2 x - 1 = 0$ ，则 $3 x^{3} - 10 x^{2} + 5 x + 2027$ 的值等于．

查看试题解析
20. 如图，图中数字是从1开始按箭头方向排列的有序数阵．从3开始，把位于同一列且在拐角处的两个数字提取出来组成有序数对： $(3 ， 5)$ ； $(7 ， 10)$ ； $(13 ， 17)$ ； $(21 ， 26)$ ； $(31 ， 37)$ …如果单把每个数对中的第一个或第二个数字按顺序排列起来研究，就会发现其中的规律．请写出第n个数对：．

查看试题解析
21. 在平面直角坐标系中， $△ A O B$ 为等边三角形，点A的坐标为 $(1 ， 0)$ ．把 $△ A O B$ 按如图所示的方式放置，并将 $△ A O B$ 进行变换：第一次变换将 $△ A O B$ 绕着原点O顺时针旋转 $60 °$ ，同时边长扩大为 $△ A O B$ 边长的2倍，得到 $△ A_{1} O B_{1}$ ；第二次旋转将 $△ A_{1} O B_{1}$ 绕着原点O顺时针旋转 $60 °$ ，同时边长扩大为 $△ A_{1} O B_{1}$ ，边长的2倍，得到 $△ A_{2} O B_{2}$ ， …．依次类推，得到 $△ A_{2033} O B_{2033}$ ，则 $△ A_{2023} O B_{2033}$ 的边长为，点 $A_{2023}$ 的坐标为．

查看试题解析
22. 在平面直角坐标系中，点 $A_{1} 、 A_{2} 、 A_{3} 、 A_{4} ⋯$ 在 $x$ 轴的正半轴上，点 $B_{1} 、 B_{2} 、 B_{3} ⋯$ 在直线 $y = \frac{\sqrt{3}}{3} x (x \geq 0)$ 上，若点 $A_{1}$ 的坐标为 $(2 ， 0)$ ，且 $△ A_{1} B_{1} A_{2} 、 △ A_{2} B_{2} A_{3} 、 △ A_{3} B_{3} A_{4} ⋯$ 均为等边三角形．则点 $B_{2023}$ 的纵坐标为．

查看试题解析
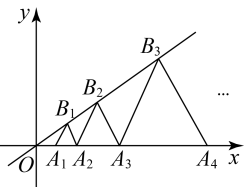23. 定义：如果一个正整数能表示为两个正整数m，n的平方差，且 $m - n > 1$ ，则称这个正整数为“智慧优数”.例如， $16 = 5^{2} - 3^{2}$ ， 16就是一个智慧优数，可以利用 $m^{2} - n^{2} = (m + n) (m - n)$ 进行研究.若将智慧优数从小到大排列，则第3个智慧优数是；第23个智慧优数是.

查看试题解析
24. 如果一个四位自然数 $\bar{a b c d}$ 的各数位上的数字互不相等且均不为0，满足 $\bar{a b} - \bar{b c} = \bar{c d}$ ，那么称这个四位数为“递减数”．例如：四位数4129，∵ $41 - 12 = 29$ ， ∴4129是“递减数”；又如：四位数5324，∵ $53 - 32 = 21 \neq 24$ ， ∴5324不是“递减数”．若一个“递减数”为 $\bar{a 312}$ ，则这个数为；若一个“递减数”的前三个数字组成的三位数 $\bar{a b c}$ 与后三个数字组成的三位数 $\bar{b c d}$ 的和能被9整除，则满足条件的数的最大值是．

查看试题解析
25. 对于一个四位自然数M，若它的千位数字比个位数字多6，百位数字比十位数字多2，则称M为“天真数”．如：四位数7311，∵ $7 - 1 = 6$ ， $3 - 1 = 2$ ， ∴7311是“天真数”；四位数8421，∵ $8 - 1 \neq 6$ ， ∴8421不是“天真数”，则最小的“天真数”为；一个“天真数”M的千位数字为a，百位数字为b，十位数字为c，个位数字为d，记 $P (M) = 3 (a + b) + c + d$ ， $Q (M) = a - 5$ ，若 $\frac{P (M)}{Q (M)}$ 能被10整除，则满足条件的M的最大值为．

查看试题解析

三、综合题

26. 对于任意实数a，b，定义一种新运算： $a ※ b = {\begin{array}{l} a - b & (a \geq 2 b) \\ a + b - 6 & (a < 2 b) \end{array}$ ，例如： $3 ※ 1 = 3 - 1 = 2$ ， $5 ※ 4 = 5 + 4 - 6 = 3$ ．根据上面的材料，请完成下列问题：

(1)、 $4 ※ 3 =$ ， $(- 1) ※ (- 3) =$ ；

(2)、若 $(3 x + 2) ※ (x - 1) = 5$ ，求x的值．

查看试题解析
27. 我们规定：对于任意实数a、b、c、d有 $[a ， b] * [c ， d] = a c - b d$ ，其中等式右边是通常的乘法和减法运算，如： $[3 ， 2] * [5 ， 1] = 3 \times 5 - 2 \times 1 = 13$ ．

(1)、求 $[- 4 ， 3] * [2 ， - 6]$ 的值；

(2)、已知关于x的方程 $[x ， 2 x - 1] * [m x + 1 ， m] = 0$ 有两个实数根，求m的取值范围．

查看试题解析
28. 观察下面的等式： $3^{2} - 1^{2} = 8 \times 1 ， 5^{2} - 3^{2} = 8 \times 2 ， 7^{2} - 5^{2} = 8 \times 3 ， 9^{2} - 7^{2} = 8 \times 4 ， ⋯$

(1)、写出 $1 9^{2} - 1 7^{2}$ 的结果．

(2)、按上面的规律归纳出一个一般的结论（用含n的等式表示，n为正整数）

(3)、请运用有关知识，推理说明这个结论是正确的．

查看试题解析
29. 某数学兴趣小组运用《几何画板》软件探究y=ax²（a＞0）型抛物线图象．发现：如图1所示，该类型图象上任意一点P到定点F（0， $\frac{1}{4 a}$ ）的距离PF，始终等于它到定直线l：y= $- \frac{1}{4 a}$ 的距离PN　（该结论不需要证明）．他们称：定点F为图象的焦点，定直线l为图象的准线，y= $- \frac{1}{4 a}$ 叫做抛物线的准线方程．准线l与y轴的交点为H．其中原点O为FH的中点，FH=2OF= $\frac{1}{2 a}$ ．例如，抛物线y=2x² ，其焦点坐标为F（0， $\frac{1}{8}$ ），准线方程为l：y= $- \frac{1}{8}$ ，其中PF=PN，FH=2OF= $\frac{1}{4}$ ．

(1)、【基础训练】请分别直接写出抛物线y= $\frac{1}{4} x^{2}$ 的焦点坐标和准线l的方程：，；

(2)、【技能训练】如图2，已知抛物线y= $\frac{1}{4} x^{2}$ 上一点P（x₀ ， y₀）（x₀＞0）到焦点F的距离是它到x轴距离的3倍，求点P的坐标；

(3)、【能力提升】如图3，已知抛物线y= $\frac{1}{4} x^{2}$ 的焦点为F，准线方程为l．直线m：y= $\frac{1}{2} x - 3$ 交y轴于点C，抛物线上动点P到x轴的距离为d₁ ，到直线m的距离为d₂ ，请直接写出d₁+d₂的最小值；

(4)、【拓展延伸】该兴趣小组继续探究还发现：若将抛物线y=ax²（a＞0）平移至y=a(x-h)²+k（a＞0）．
抛物线y=a(x-h)²+k（a＞0）内有一定点F（h， $k + \frac{1}{4 a}$ ），直线l过点M（h， $k - \frac{1}{4 a}$ ）且与x轴平行．当动点P在该抛物线上运动时，点P到直线l的距离PP₁始终等于点P到点F的距离（该结论不需要证明）．例如：抛物线y=2(x-1)²+3上的动点P到点F（1， $\frac{25}{8}$ ）的距离等于点P到直线l：y= $\frac{23}{8}$ 的距离．

请阅读上面的材料，探究下题：

如图4，点D（-1， $\frac{3}{2}$ ）是第二象限内一定点，点P是抛物线y= $\frac{1}{4} x^{2}$ -1上一动点．当PO+PD取最小值时，请求出△POD的面积．

查看试题解析