2023年浙教版数学九年级上册3.1 圆 同步测试(培优版)
试卷更新日期:2023-07-18 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图是两个大小不同的量角器.小量角器由于长时间使用,某些刻度已经模糊不清.现将两个量角器的零刻度线放在同一直线上,使与C重合(如下图).如果两个半圆的公共点P在大量角器上对应的度数为 , 那么在小量角器上对应的度数为( )
 A、 B、 C、 D、2. 如图,圆上有两点 , , 连结 , 分别以 , 为圆心,的长为半径画弧,两弧相交于点交于点E,交于点F,若 , 则该圆的半径长是( )
A、 B、 C、 D、2. 如图,圆上有两点 , , 连结 , 分别以 , 为圆心,的长为半径画弧,两弧相交于点交于点E,交于点F,若 , 则该圆的半径长是( ) A、10 B、6 C、5 D、43. 一块某市政府特别奖奖牌如图所示,点A、B、D在圆O上,CD垂直平分AB于点C.现测得AB=CD=16cm,则圆形奖牌的半径为( )
A、10 B、6 C、5 D、43. 一块某市政府特别奖奖牌如图所示,点A、B、D在圆O上,CD垂直平分AB于点C.现测得AB=CD=16cm,则圆形奖牌的半径为( )
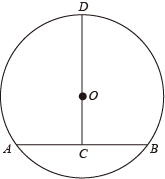 A、12cm B、10cm C、8cm D、6cm4. 如图,半径为3的⊙O内有一点A,OA= ,点P在⊙O上,当∠OPA最大时,PA的长等于( )
A、12cm B、10cm C、8cm D、6cm4. 如图,半径为3的⊙O内有一点A,OA= ,点P在⊙O上,当∠OPA最大时,PA的长等于( ) A、 B、 C、3 D、25. 如图,四边形为矩形, , .点P是线段上一动点,点M为线段上一点. , 则的最小值为( )
A、 B、 C、3 D、25. 如图,四边形为矩形, , .点P是线段上一动点,点M为线段上一点. , 则的最小值为( ) A、 B、 C、 D、6. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个7. 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0).点M是P上的动点,点C是MB的中点,则AC的最小值为( )
A、 B、 C、 D、6. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个7. 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0).点M是P上的动点,点C是MB的中点,则AC的最小值为( ) A、14 B、 C、 D、268. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( )
A、14 B、 C、 D、268. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( ) A、4 B、8 C、10 D、69. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( )
A、4 B、8 C、10 D、69. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( ) A、72 B、96 C、120 D、14410. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A、72 B、96 C、120 D、14410. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( ) A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心
A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心二、填空题(每空4分,共24分)
-
11. 一个直角三角形的两条边长是方程x2﹣7x+12=0的两个根,则此直角三角形的外接圆的直径为.12. 如图所示,在平面直角坐标系xOy中,点P是钝角的外心,点A、B、P的坐标分别为 , , , 若第一象限的点C横坐标、纵坐标均为整数,则点C的坐标为 .
 13. 我们知道平面内到两个定点距离之比为常数(常数大于零且不为1)的点轨迹是一个圆,那么在平面直角坐标系内到原点(0,0)和点(3,0)距离之比为2的圆的圆心坐标是.
13. 我们知道平面内到两个定点距离之比为常数(常数大于零且不为1)的点轨迹是一个圆,那么在平面直角坐标系内到原点(0,0)和点(3,0)距离之比为2的圆的圆心坐标是.
14. 下面是“作出弧AB所在的圆”的尺规作图过程.已知:弧AB.
求作:弧AB所在的圆.
作法:如图,
⑴在弧AB上任取三个点D,C,E;
⑵连接DC,EC;
⑶分别作DC和EC的垂直平分线,两垂直平分线的交点为点O.
⑷以 O为圆心,OC长为半径作圆,所以⊙O即为所求作的弧AB所在的圆.
请回答:该尺规作图的依据是 .
 15. 如图,⊙M的半径为4,圆心M的坐标为(5,12),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为.
15. 如图,⊙M的半径为4,圆心M的坐标为(5,12),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为.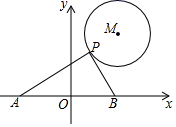 16. 如图,点A,B的坐标分别为 , ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为 .
16. 如图,点A,B的坐标分别为 , ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为 .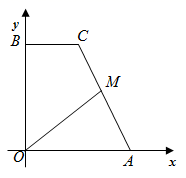
三、解答题(共5题,共46分)
-
17. 已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
 18. 如图,C是AB上一点,点D、E分别位于AB的异侧,AD∥BE,且AD=BC,AC=BE.
18. 如图,C是AB上一点,点D、E分别位于AB的异侧,AD∥BE,且AD=BC,AC=BE.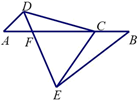 (1)、求证:CD=CE;(2)、当 时,求BF的长;(3)、若∠A=α,∠ACD=25°,且△CDE的外心在该三角形的外部,请直接写出α的取值范围.19. 有三条长度均为a的线段,分别按以下要求画圆.
(1)、求证:CD=CE;(2)、当 时,求BF的长;(3)、若∠A=α,∠ACD=25°,且△CDE的外心在该三角形的外部,请直接写出α的取值范围.19. 有三条长度均为a的线段,分别按以下要求画圆.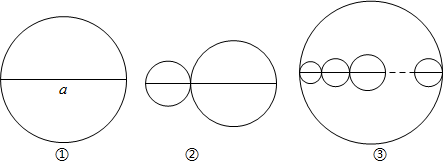 (1)、如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2 , 请指出C1和C2的数量关系,并说明理由;(2)、如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若干小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为.(直接填写答案,结果保留π)20.
(1)、如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2 , 请指出C1和C2的数量关系,并说明理由;(2)、如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若干小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为.(直接填写答案,结果保留π)20.
(1)、问题提出如图1,点A为线段BC外一动点,且 ,填空:当点A位于时,线段AC的长取得最大值,且最大值为 用含 的式子表示 .
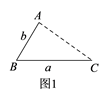 (2)、问题探究
(2)、问题探究点A为线段BC外一动点,且 ,如图2所示,分别以 为边,作等边三角形ABD和等边三角形ACE,连接 ,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
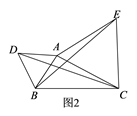 (3)、问题解决:
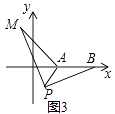
(3)、问题解决:①如图3,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,点P为线段AB外一动点,且 ,求线段AM长的最大值及此时点P的坐标.
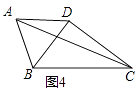
如图4,在四边形ABCD中, ,若对角线 于点D,请直接写出对角线AC的最大值.
 21. 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段 为直径的圆.(1)、请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
21. 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段 为直径的圆.(1)、请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);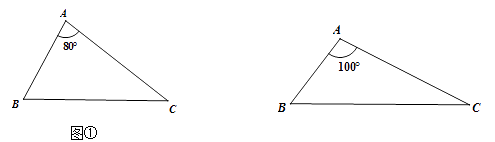 (2)、三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);(3)、某城市有四个小区 (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(2)、三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);(3)、某城市有四个小区 (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.