2023年高考数学真题分类汇编4：排列组合与概率统计、算法与框图

试卷更新日期：2023-07-18 类型：二轮复习

进入出卷网下载

一、填空题

1. 在 ${(2 x^{3} - \frac{1}{x})}^{6}$ 的展开式中， $x^{2}$ 项的系数为．

查看试题解析
2. 甲乙丙三个盒子中装有一定数量的黑球和白球，其总数之比为 $5 ： 4 ： 6$ ．这三个盒子中黑球占总数的比例分别为 $40 % ， 25 % ， 50 %$ ．现从三个盒子中各取一个球，取到的三个球都是黑球的概率为；将三个盒子混合后任取一个球，是白球的概率为．

查看试题解析
3. 空间内存在三点 $A 、 B 、 C$ ，满足 $A B = A C = B C = 1$ ，在空间内取不同两点(不计顺序)，使得这两点与 $A 、 B 、 C$ 可以组成正四棱锥，求方案数为；

查看试题解析
4. 已知 ${(1 + 2023 x)}^{100} + {(2023 - x)}^{100} = a_{0} + a_{1} x + a_{2} x^{2} + ⋯ + a_{100} x^{100}$ ，其中 $a_{0} ， a_{1} ， a_{2} ⋯ a_{100} \in ℝ$ ，若 $0 \leq k \leq 100$ 且 $k \in ℕ$ ，当 $a_{k} < 0$ 时， $k$ 的最大值是；

查看试题解析
5. 国内生产总值(GDP)是衡量地区经济状况的最佳指标，根据统计数据显示，某市在2020年间经济高质量增长，GDP稳步增长，第一季度和第四季度的GDP分别为231和242，且四个季度GDP的中位数与平均数相等，则2020年GDP总额为；

查看试题解析
6. 某学校开设了4门体育类选修课和4门艺术类选修课，学生需从这8门课中选修2门或3门课，并且每类选修课至少选修1门，则不同的选课方案共有种(用数字作答).

查看试题解析

二、选择题

7. 有50人报名足球俱乐部，60人报名乒乓球俱乐部，70人报名足球或乒乓球俱乐部，若已知某人报足球俱乐部，则其报乒乓球俱乐部的概率为（）

A、0.8 B、0.4 C、0.2 D、0.1

查看试题解析
8. 有五名志愿者参加社区服务，共服务星期六、星期天两天，每天从中任选两人参加服务，则恰有1人连续参加两天服务的选择种数为（）

A、120 B、60 C、40 D、30

查看试题解析
9. 某校文艺部有4名学生，其中高一、高二年级各2名．从这4名学生中随机选2名组织校文艺汇演，则这2名学生来自不同年级的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
10. 执行下面的程序框遇，输出的 $B =$ （）

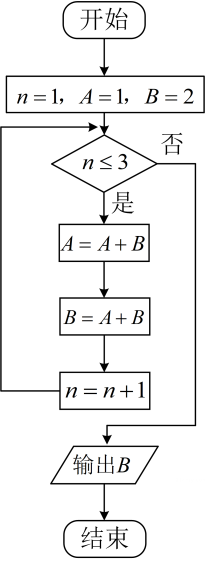A、21 B、34 C、55 D、89

查看试题解析
11. 执行下边的程序框图，则输出的 $B =$ （）

A、21 B、34 C、55 D、89

查看试题解析
12. 调查某种群花萼长度和花瓣长度，所得数据如图所示，其中相关系数 $r = 0.8245$ ，下列说法正确的是（）

A、花瓣长度和花萼长度没有相关性 B、花瓣长度和花萼长度呈现负相关 C、花瓣长度和花萼长度呈现正相关 D、若从样本中抽取一部分，则这部分的相关系数一定是 $0.8245$

查看试题解析
13. 设O为平面坐标系的坐标原点，在区域 ${(x ， y) | 1 \leq x^{2} + y^{2} \leq 4}$ 内随机取一点，记该点为A，则直线OA的倾斜角不大于 $\frac{π}{4}$ 的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
14. 甲乙两位同学从6种课外读物中各自选读2种，则这两人选读的课外读物中恰有1种相同的选法共有（）

A、30种 B、60种 C、120种 D、240种

查看试题解析
15. 设O为平面坐标系的坐标原点，在区域 ${(x ， y) | 1 \leq x^{2} + y^{2} \leq 4}$ 内随机取一点A，则直线OA的倾斜角不大于 $\frac{π}{4}$ 的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
16. 某学校举办作文比赛，共6个主题，每位参赛同学从中随机抽取一个主题准备作文，则甲、乙两位参赛同学抽到不同主题概率为（）

A、 $\frac{5}{6}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
17. 根据身高和体重散点图，下列说法正确的是（）.

A、身高越高，体重越重 B、身高越高，体重越轻 C、身高与体重成正相关 D、身高与体重成负相关

查看试题解析
18. 在信道内传输0，1信号，信号的传输相互独立.发送0时，收到1的概率为 $α (0 < α < 1)$ ，收到0的概率为 $1 - α$ ；发送1时，收到0的概率为 $β (0 < β < 1)$ ，收到1的概率为 $1 - β$ .考虑两种传输方案：单次传输和三次传输.单次传输是指每个信号只发送1次，三次传输是指每个信号重复发送3次，收到的信号需要译码，译码规则如下：单次传输时，收到的信号即为译码：三次传输时，收到的信号中出现次数多的即为译码(例如，若依次收到1，0，1，则译码为1)

A、采用单次传输方案，若依次发送1，0，1，则依次收到1，0，1的概率为 $(1 - α) (1 - β)^{2}$ B、采用三次传输方案，若发送1，则依次收到 1，0，1的概率为 $β (1 - β)^{2}$ C、采用三次传输方案，若发送1，则译码为1的概率为 $β (1 - β)^{2} (1 - β)^{3}$ D、当 $0 < α < 0.5$ 时，若发送0，则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率

查看试题解析
19. 某学校为了了解学生参加体育运动的情况，用比例分配的分层随机抽样法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同抽样结果共有（）.

A、 $C_{400}^{45} \cdot C_{200}^{15}$ 种 B、 $C_{400}^{20} \cdot C_{200}^{40}$ 种 C、 $C_{400}^{30} \cdot C_{200}^{30}$ 种 D、 $C_{400}^{40} \cdot C_{200}^{20}$ 种

查看试题解析
20. 有一组样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{6}$ ，其中 $x_{1}$ 是最小值， $x_{6}$ 是最大值，则（）

A、 $x_{2} ， x_{3} ， x_{4} ， x_{5}$ 的平均数等于 $x_{1} ， x_{2} ， ⋯ ， x_{6}$ 的平均数 B、 $x_{2} ， x_{3} ， x_{4} ， x_{5}$ 的中位数等于 $x_{1} ， x_{2} ， ⋯ ， x_{6}$ 的中位数 C、 $x_{2} ， x_{3} ， x_{4} ， x_{5}$ 的标准差不小于 $x_{1} ， x_{2} ， ⋯ ， x_{6}$ 的标准差 D、 $x_{2} ， x_{3} ， x_{4} ， x_{5}$ 的极差不大于 $x_{1} ， x_{2} ， ⋯ ， x_{6}$ 的极差

查看试题解析

三、解答题

21. 一项试验旨在研究臭氧效应，试验方案如下：选40只小白鼠，随机地将其中20只分配到试验组，另外20只分配到对照组，试验组的小白鼠饲养在高浓度臭氧环境，对照组的小白鼠饲养在正常环境，一段时间后统计每只小白鼠体重的增加量（单位：g）．试验结果如下：
对照组的小白鼠体重的增加量从小到大排序为

15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1

32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2

试验组的小白鼠体重的增加量从小到大排序为

7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2

19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5

(1)、计算试验组的样本平均数；

(2)、（ⅰ）求40只小白鼠体重的增加量的中位数m，再分别统计两样本中小于m与不小于m的数据的个数，完成如下列联表

$< m$

$\geq m$

对照组

试验组

（ⅱ）根据（i）中的列联表，能否有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异？

附： $K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

$P (K^{2} \geq k)$

0.100

0.050

0.010

$k$

2.706

3.841

6.635

查看试题解析
22. 为探究某药物对小鼠的生长抑制作用，将40只小鼠均分为两组，分别为对照组（不加药物）和实验组（加药物）．

(1)、设其中两只小鼠中对照组小鼠数目为 $X$ ，求 $X$ 的分布列和数学期望；

(2)、测得40只小鼠体重如下（单位：g）：（已按从小到大排好）
对照组：17.3 18.4 20.1 20.4 21.5 23.2 24.6 24.8 25.0 25.4

26.1 26.3 26.4 26.5 26.8 27.0 27.4 27.5 27.6 28.3

实验组：5.4 6.6 6.8 6.9 7.8 8.2 9.4 10.0 10.4 11.2

14.4 17.3 19.2 20.2 23.6 23.8 24.5 25.1 25.2 26.0

（i）求40只小鼠体重的中位数m，并完成下面2×2列联表：

<m >m 合计

对照组

实验组

合计

（ii）根据2×2列联表，能否有95%的把握认为药物对小鼠生长有抑制作用．

参考数据：

$k_{0}$ 0.10 0.05 0.010

$P (k^{2} \geq k_{0})$ 2.706 3.841 6.635

查看试题解析

23. 某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应，进行10次配对试验，每次配对试验选用材质相同的两个橡胶产品，随机地选其中一个用甲工艺处理，另一个用乙工艺处理，测量处理后的橡胶产品的伸缩率，甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为

x_{i}

，

y_{i}

（

i = 1 ， 2 ， \cdot \cdot \cdot 10

），试验结果如下

试验序号i	1	2	3	4	5	6	7	8	9	10
伸缩率 $x_{i}$	545	533	551	522	575	544	541	568	596	548
伸缩率 $y_{i}$	536	527	543	530	560	533	522	550	576	536

记 $z_{i} = x_{i} - y_{i} (i = 1 ， 2 ， ⋯ ， 10)$ ，记 $z_{1}$ ， $z_{2}$ ， …， $z_{10}$ 的样本平均数为 $\bar{z}$ ，样本方差为 $s^{2}$ ，

(1)、求

\bar{z}

，

s^{2}

；

(2)、判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高（如果

\bar{z} \geq 2 \sqrt{\frac{s^{2}}{10}}

，则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高，否则不认为有显著提高）.

查看试题解析

24. 某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应，进行10次配对试验，每次配对试验选用材质相同的两个橡胶产品，随机地选其中一个用甲工艺处理，另一个用乙工艺处理，测量处理后的橡胶产品的伸缩率．甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为

x_{i}

，

y_{i} (i = 1 ， 2 ， \cdot \cdot \cdot ， 10)

．试验结果如下：

试验序号 $i$	1	2	3	4	5	6	7	8	9	10
伸缩率 $x_{i}$	545	533	551	522	575	544	541	568	596	548
伸缩率 $y_{i}$	536	527	543	530	560	533	522	550	576	536

记 $z_{i} = x_{i} - y_{i} (i = 1 ， 2 ， \cdot \cdot \cdot ， 10)$ ，记 $z_{1} ， z_{2} ， \cdot \cdot \cdot ， z_{10}$ 的样本平均数为 $\bar{z}$ ，样本方差为 $s^{2}$ ．

(1)、求

\bar{z}

，

s^{2}

；

(2)、判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高（如果

\bar{z} \geq 2 \sqrt{\frac{s^{2}}{10}}

，则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高，否则不认为有显著提高）

查看试题解析

25. 21世纪汽车博览会在上海2023年6月7日在上海举行，下表为某汽车模型公司共有25个汽车模型，其外观和内饰的颜色分布如下表所示：

红色外观
蓝色外观
棕色内饰
12
8
米色内饰
2
3

(1)、若小明从这些模型中随机拿一个模型，记事件 $A$ 为小明取到的模型为红色外观，事件B为取到模型有棕色内饰.
求 $P (B) 、 P (B / A)$ ，并据此判断事件 $A$ 和事件 $B$ 是否独立；

(2)、该公司举行了一个抽奖活动，规定在一次抽奖中，每人可以一次性从这些模型中拿两个汽车模型，给出以下假设：
假设1：拿到的两个模型会出现三种结果，即外观和内饰均为同色、外观内饰都异色、以及仅外观或仅内饰同色；

假设2：按结果的可能性大小，概率越小奖项越高；

假设3：奖金额为一等奖600元，二等奖300元，三等奖150元；

请你分析奖项对应的结果，设 $X$ 为奖金额，写出 $X$ 的分布列并求出 $X$ 的数学期望

查看试题解析
26. 某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异，经过大量调查，得到如下的患病者和未患病者该指标的频率分布直方图：

利用该指标制定一个检测标准，需要确定临界值c，将该指标大于c的人判定为阳形，小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率，记为 $p (c)$ ；误诊率是将未患病者判定为阳性的概率，记为 $q (c)$ .假设数据在组内均匀分布.以事件发生的频率作为相应事件发生的概率.

(1)、当漏诊率 $P (c) = 0.5 %$ 时，求临近值c和误诊率 $q (c)$ ；

(2)、设函数 $f (c) = p (c) + q (c)$ ，当 $c \in [95 ， 105]$ 时，求 $f (c)$ 的解析式，并求 $f (c)$ 在区间 $[95 ， 105]$ 的最小值.

查看试题解析
27. 甲乙两人投篮，每次由其中一人投篮，规则如下：若命中则此人继续投篮，若未命中则换为对方投篮.无论之前投篮情况如何，甲每次投篮的命中率均为0.6，乙每次投篮的命中率均为0.8，由抽签决定第一次投篮的人选，第一次投篮的人是甲，乙的概率各为0.5.

(1)、求第2次投篮的人是乙的概率；

(2)、求第i次投篮的人是甲的概率；

(3)、已知：若随机变量 $X_{i}$ 服从两点分布，且 $P (X_{i} = 1) = 1 - P (X_{i} = 0) = q_{i} ， i =$ $1 ， 2 ， ⋯ ， n$ ，则 $E (\sum_{i = 1}^{n} X_{i}) = \sum_{i = 1}^{n} q_{i}$ ，记前 $n$ 次 (即从第1次到第 $n$ 次投篮)中甲投篮的次数为 $Y$ ，求 $E (Y)$ .

查看试题解析

	$< m$	$\geq m$
对照组
试验组

$P (K^{2} \geq k)$	0.100	0.050	0.010
$k$	2.706	3.841	6.635

	<m	>m	合计
对照组
实验组
合计

$k_{0}$	0.10	0.05	0.010
$P (k^{2} \geq k_{0})$	2.706	3.841	6.635