辽宁省大连市2023年中考数学试卷
试卷更新日期:2023-07-17 类型:中考真卷
一、选择题(本题共10小题,每小3分,共30分,在每小题给出的四个选项中,只有1个选项正确)
-
1. -6的绝对值是( )A、-6 B、6 C、- D、2. 如图所示的几何体中,主视图是( )
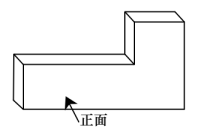 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,直线 , 则的度数为( )
3. 如图,直线 , 则的度数为( ) A、 B、 C、 D、4. 某种离心机的最大离心力为 . 数据用科学记数法表示为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 将方程去分母,两边同乘后的式子为( )A、 B、 C、 D、7. 已知蓄电池两端电压为定值,电流与成反比例函数关系.当时, , 则当时,的值为( )A、 B、 C、 D、8. 圆心角为 , 半径为3的扇形弧长为( )A、 B、 C、 D、9. 已知抛物线 , 则当时,函数的最大值为( )A、 B、 C、0 D、210. 某小学开展课后服务,其中在体育类活动中开设了四种运动项目:乒乓球、排球、篮球、足球.为了解学生最喜欢哪一种运动项目,随机选取100名学生进行问卷调查(每位学生仅选一种),并将调查结果绘制成如下的扇形统计图.下列说法错误的是( )
A、 B、 C、 D、4. 某种离心机的最大离心力为 . 数据用科学记数法表示为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 将方程去分母,两边同乘后的式子为( )A、 B、 C、 D、7. 已知蓄电池两端电压为定值,电流与成反比例函数关系.当时, , 则当时,的值为( )A、 B、 C、 D、8. 圆心角为 , 半径为3的扇形弧长为( )A、 B、 C、 D、9. 已知抛物线 , 则当时,函数的最大值为( )A、 B、 C、0 D、210. 某小学开展课后服务,其中在体育类活动中开设了四种运动项目:乒乓球、排球、篮球、足球.为了解学生最喜欢哪一种运动项目,随机选取100名学生进行问卷调查(每位学生仅选一种),并将调查结果绘制成如下的扇形统计图.下列说法错误的是( ) A、本次调查的样本容量为100 B、最喜欢篮球的人数占被调查人数的 C、最喜欢足球的学生为40人 D、“排球”对应扇形的圆心角为
A、本次调查的样本容量为100 B、最喜欢篮球的人数占被调查人数的 C、最喜欢足球的学生为40人 D、“排球”对应扇形的圆心角为二、填空题(本题共6小题,每小题3分,共18分)
-
11. 的解集为 .12. 一个袋子中装有两个标号为“1”“2”的球.从中任意摸出一个球,记下标号后放回并再次摸出一个球,记下标号后放回.则两次标号之和为3的概率为 .13. 如图,在菱形中,为菱形的对角线, , 点为中点,则的长为 .
 14. 如图,在数轴上, , 过作直线于点 , 在直线上截取 , 且在上方.连接 , 以点为圆心,为半径作弧交直线于点 , 则点的横坐标为 .
14. 如图,在数轴上, , 过作直线于点 , 在直线上截取 , 且在上方.连接 , 以点为圆心,为半径作弧交直线于点 , 则点的横坐标为 . 15. 我国的《九章算术》中记载道:“今有共买物,人出八,盈三;人出七,不足四.问有几人.”大意是:今有人合伙购物,每人出元钱,会多钱;每人出元钱,又差钱,问人数有多少.设有人,则可列方程为: .16. 如图,在正方形中, , 延长至 , 使 , 连接 , 平分交于 , 连接 , 则的长为 .
15. 我国的《九章算术》中记载道:“今有共买物,人出八,盈三;人出七,不足四.问有几人.”大意是:今有人合伙购物,每人出元钱,会多钱;每人出元钱,又差钱,问人数有多少.设有人,则可列方程为: .16. 如图,在正方形中, , 延长至 , 使 , 连接 , 平分交于 , 连接 , 则的长为 .
三、解答题(本题共4小题,其中17题9分,18、19、20题各10分,共39分)
-
17. 计算: .18. 某服装店的某件衣服最近销售火爆.现有两家供应商到服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:),并对数据进行整理、描述和分析.部分信息如下:
Ⅰ.供应商供应材料的纯度(单位:)如下:
72
73
74
75
76
78
79
频数
1
1
5
3
3
1
1
Ⅱ.供应商供应材料的纯度(单位:)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 72 75
Ⅲ.两供应商供应材料纯度的平均数、中位数、众数和方差如下:
平均数
中位数
众数
方差
75
75
74
3.07
75
根据以上信息,回答下列问题:
(1)、表格中的 , , ;(2)、你认为服装店应选择哪个供应商供应服装?为什么?19. 如图,在和中,延长交于 , , . 求证: . 20. 为了让学生养成热爱图书的习惯,某学校抽出一部分资金用于购买书籍.已知2020年该学校用于购买图书的费用为5000元,2022年用于购买图书的费用是7200元,求年买书资金的平均增长率.
20. 为了让学生养成热爱图书的习惯,某学校抽出一部分资金用于购买书籍.已知2020年该学校用于购买图书的费用为5000元,2022年用于购买图书的费用是7200元,求年买书资金的平均增长率.四、解答题(本题共3小题,其中21题9分,22、23题各10分,共29分)
-
21. 如图所示是消防员攀爬云梯到小明家的场景.已知 , , 点关于点的仰角为 , 则楼的高度为多少?(结果保留整数.参考数据:)
 22. 为了增强学生身体素质,学校要求男女同学练习跑步.开始时男生跑了 , 女生跑了 , 然后男生女生都开始匀速跑步.已知男生的跑步速度为 , 当到达终点时男、女均停止跑步,男生从开始匀速跑步到停止跑步共用时 . 已知轴表示从开始匀速跑步到停止跑步的时间,轴代表跑过的路程,则:
22. 为了增强学生身体素质,学校要求男女同学练习跑步.开始时男生跑了 , 女生跑了 , 然后男生女生都开始匀速跑步.已知男生的跑步速度为 , 当到达终点时男、女均停止跑步,男生从开始匀速跑步到停止跑步共用时 . 已知轴表示从开始匀速跑步到停止跑步的时间,轴代表跑过的路程,则: (1)、男女跑步的总路程为 .(2)、当男、女相遇时,求此时男、女同学距离终点的距离.23. 如图1,在中,为的直径,点为上一点,为的平分线交于点 , 连接交于点 .
(1)、男女跑步的总路程为 .(2)、当男、女相遇时,求此时男、女同学距离终点的距离.23. 如图1,在中,为的直径,点为上一点,为的平分线交于点 , 连接交于点 . (1)、求的度数;(2)、如图2,过点作的切线交延长线于点 , 过点作交于点 . 若 , 求的长.
(1)、求的度数;(2)、如图2,过点作的切线交延长线于点 , 过点作交于点 . 若 , 求的长.五、解答题(本题共3小题,其中24、25题各11分,26题12分,共34分)
-
24. 如图1,在平面直角坐标系中,直线与直线相交于点 , 为线段上一动点(不与点重合),过点作轴交直线于点 . 与的重叠面积为 . 关于的函数图象如图2所示.
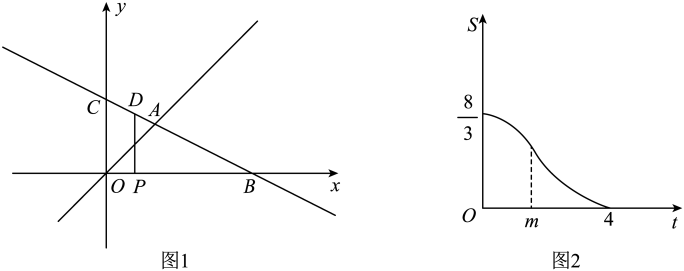 (1)、的长为;的面积为 .(2)、求关于的函数解析式,并直接写出自变量的取值范围.25. 综合与实践
(1)、的长为;的面积为 .(2)、求关于的函数解析式,并直接写出自变量的取值范围.25. 综合与实践问题情境:数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质.
已知 , 点为上一动点,将以为对称轴翻折.同学们经过思考后进行如下探究:
独立思考:小明:“当点落在上时, . ”
小红:“若点为中点,给出与的长,就可求出的长.”
实践探究:奋进小组的同学们经过探究后提出问题1,请你回答:

问题1:在等腰中,由翻折得到.
(1)、如图1,当点落在上时,求证:;(2)、如图2,若点为中点, , 求的长.问题解决:小明经过探究发现:若将问题1中的等腰三角形换成的等腰三角形,可以将问题进一步拓展.
问题2:如图3,在等腰中, . 若 , 则求的长.
26. 如图,在平面直角坐标系中,抛物线上有两点 , 其中点的横坐标为 , 点的横坐标为 , 抛物线过点 . 过作轴交抛物线另一点为点 . 以长为边向上构造矩形 . (1)、求抛物线的解析式;(2)、将矩形向左平移个单位,向下平移个单位得到矩形 , 点的对应点落在抛物线上.
(1)、求抛物线的解析式;(2)、将矩形向左平移个单位,向下平移个单位得到矩形 , 点的对应点落在抛物线上.①求关于的函数关系式,并直接写出自变量的取值范围;
②直线交抛物线于点 , 交抛物线于点 . 当点为线段的中点时,求的值;
③抛物线与边分别相交于点 , 点在抛物线的对称轴同侧,当时,求点的坐标.