辽宁省营口市2023年中考数学试卷
试卷更新日期:2023-07-17 类型:中考真卷
一、选择题(下列各题的备选答案中,只有一个是正确的,每小题3分,共30分)
-
1. 的绝对值是( )A、 B、 C、 D、2. 如图是由五个相同的正方体搭成的几何体,这个几何体的主视图是( )
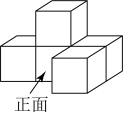 A、
A、 B、
B、 C、
C、 D、
D、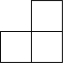 3. 有下列四个算式①;②;③;④ . 其中,正确的有( ).A、0个 B、1个 C、2个 D、3个4. 如图,是的平分线, , , 则的度数是( )
3. 有下列四个算式①;②;③;④ . 其中,正确的有( ).A、0个 B、1个 C、2个 D、3个4. 如图,是的平分线, , , 则的度数是( ) A、50° B、40° C、35° D、45°5. 下列计算结果正确的是( )A、 B、 C、 D、6. 下列事件是必然事件的是( )A、四边形内角和是360° B、校园排球比赛,九年一班获得冠军 C、掷一枚硬币时,正面朝上 D、打开电视,正在播放神舟十六号载人飞船发射实况7. 不等式组的解集在数轴上表示正确的是( )A、
A、50° B、40° C、35° D、45°5. 下列计算结果正确的是( )A、 B、 C、 D、6. 下列事件是必然事件的是( )A、四边形内角和是360° B、校园排球比赛,九年一班获得冠军 C、掷一枚硬币时,正面朝上 D、打开电视,正在播放神舟十六号载人飞船发射实况7. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 2台大收割机和5台小收割机同时工作2小时共收割小麦3.6公顷,3台大收割机和2台小收割机同时工作5小时共收割小麦8公顷.1台大收割机和1台小收割机每小时各收割小麦多少公顷?设1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,根据题意,可列方程组为( )A、 B、 C、 D、9. 如图所示,是的直径,弦交于点E,连接 , 若 , 则的度数是( )
8. 2台大收割机和5台小收割机同时工作2小时共收割小麦3.6公顷,3台大收割机和2台小收割机同时工作5小时共收割小麦8公顷.1台大收割机和1台小收割机每小时各收割小麦多少公顷?设1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,根据题意,可列方程组为( )A、 B、 C、 D、9. 如图所示,是的直径,弦交于点E,连接 , 若 , 则的度数是( ) A、 B、 C、 D、10. 如图.抛物线与x轴交于点和点 , 与y轴交于点C.下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y随x的增大而增大;⑤(m为任意实数)其中正确的个数是( )
A、 B、 C、 D、10. 如图.抛物线与x轴交于点和点 , 与y轴交于点C.下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y随x的增大而增大;⑤(m为任意实数)其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每小题3分,共18分)
-
11. 若二次根式有意义,则x的取值范围是 .12. 在平面直角坐标系中,将点向左平移5个单位长度,得到点 , 则点的坐标是 .13. 某班35名同学一周课外阅读时间统计如表所示
时间/小时
7
8
9
10
人数
4
12
13
6
则该班35名同学一周课外阅读时间的众数是小时.
14. 若关于x的方程的一个根是3,则此方程的另一个根是 .15. 如图,在中,以A为圆心,长为半径作弧,交于C,D两点,分别以点C和点D为圆心,大于长为半径作弧,两弧交于点P,作直线 , 交于点E,若 , , 则 . 16. 如图,在中, , , 将绕着点C按顺时针旋转得到 , 连接BD交于在E,则 .
16. 如图,在中, , , 将绕着点C按顺时针旋转得到 , 连接BD交于在E,则 .
三、解答题(共9题,共102分)
-
17. 先化简,再求值: , 其中 .18. 某校在评选“劳动小能手”活动中,随机调查了部分学生的周末家务劳动时间,根据调查结果,将劳动时长划分为A,B,C,D四个组别,并绘制成如下不完整统计图表
学生周末家务劳动时长分组表
组别
A
B
C
D
t(小时)

请根据图表中的信息解答下列问题:
(1)、这次抽样调查共抽取名学生,条形统计图中的 , D组所在扇形的圆心角的度数是;(2)、已知该校有900名学生,根据调查结果,请你估计该校周末家务劳动时长不低于1小时的学生共有多少人?(3)、班级准备从周末家务劳动时间较长的三男一女四名学生中,随机抽取两名学生参加“我劳动,我快乐”的主题演讲活动,请用列表法或画树状图法求出恰好选中两名男生的概率.19. 如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且 , . .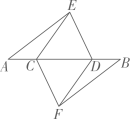 (1)、求证:;(2)、若 , , 求的长.20. 如图,点A在反比例函数的图象上,轴于点B, , .
(1)、求证:;(2)、若 , , 求的长.20. 如图,点A在反比例函数的图象上,轴于点B, , . (1)、求反比例函数的解析式;(2)、点C在这个反比例函数图象上,连接并延长交x轴于点D,且 , 求点C的坐标.21. 为了丰富学生的文化生活,学校利用假期组织学生到素质教育基地A和科技智能馆B参观学习,学生从学校出发,走到C处时,发现A位于C的北偏西方向上,B位于C的北偏西方向上,老师将学生分成甲乙两组,甲组前往A地,乙组前往B地,已知B在A的南偏西方向上,且相距1000米,请求出甲组同学比乙组同学大约多走多远的路程(参考数据: , )
(1)、求反比例函数的解析式;(2)、点C在这个反比例函数图象上,连接并延长交x轴于点D,且 , 求点C的坐标.21. 为了丰富学生的文化生活,学校利用假期组织学生到素质教育基地A和科技智能馆B参观学习,学生从学校出发,走到C处时,发现A位于C的北偏西方向上,B位于C的北偏西方向上,老师将学生分成甲乙两组,甲组前往A地,乙组前往B地,已知B在A的南偏西方向上,且相距1000米,请求出甲组同学比乙组同学大约多走多远的路程(参考数据: , ) 22. 某大型超市购进一款热销的消毒洗衣液,由于原材料价格上涨,今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元,今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同.当每瓶洗衣液的现售价为36元时,每周可卖出600瓶,为了能薄利多销.该超市决定降价销售,经市场调查发现,这种洗衣液的售价每降价1元,每周的销量可增加100瓶,规定这种消毒洗衣液每瓶的售价不低于进价.(1)、求今年这款消毒洗衣液每瓶进价是多少元;(2)、当这款消毒洗衣液每瓶的售价定为多少元时,这款洗衣液每周的销售利润最大?最大利润是多少元?23. 如图,在中, , 以为直径作与交于点D,过点D作 , 交延长线于点F,垂足为点E.
22. 某大型超市购进一款热销的消毒洗衣液,由于原材料价格上涨,今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元,今年用1440元购进这款洗衣液的数量与去年用1200元购进这款洗衣液的数量相同.当每瓶洗衣液的现售价为36元时,每周可卖出600瓶,为了能薄利多销.该超市决定降价销售,经市场调查发现,这种洗衣液的售价每降价1元,每周的销量可增加100瓶,规定这种消毒洗衣液每瓶的售价不低于进价.(1)、求今年这款消毒洗衣液每瓶进价是多少元;(2)、当这款消毒洗衣液每瓶的售价定为多少元时,这款洗衣液每周的销售利润最大?最大利润是多少元?23. 如图,在中, , 以为直径作与交于点D,过点D作 , 交延长线于点F,垂足为点E. (1)、求证:为的切线;(2)、若 , , 求的长.24. 在中, , 点E在上,点G在上,点F在的延长线上,连接 . , .
(1)、求证:为的切线;(2)、若 , , 求的长.24. 在中, , 点E在上,点G在上,点F在的延长线上,连接 . , . (1)、如图1,当时,请用等式表示线段与线段的数量关系;(2)、如图2,当时,写出线段和之间的数量关系,并说明理由;(3)、在(2)的条件下,当点G是的中点时,连接 , 求的值.25. 如图,抛物线与轴交于点和点 , 与轴交于点 , 抛物线的对称轴交轴于点 , 过点作直线轴,过点作 , 交直线于点 .
(1)、如图1,当时,请用等式表示线段与线段的数量关系;(2)、如图2,当时,写出线段和之间的数量关系,并说明理由;(3)、在(2)的条件下,当点G是的中点时,连接 , 求的值.25. 如图,抛物线与轴交于点和点 , 与轴交于点 , 抛物线的对称轴交轴于点 , 过点作直线轴,过点作 , 交直线于点 . (1)、求抛物线的解析式;(2)、如图,点为第三象限内抛物线上的点,连接和交于点 , 当时.求点的坐标;(3)、在(2)的条件下,连接 , 在直线上是否存在点 , 使得?若存在,请直接写出点F的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图,点为第三象限内抛物线上的点,连接和交于点 , 当时.求点的坐标;(3)、在(2)的条件下,连接 , 在直线上是否存在点 , 使得?若存在,请直接写出点F的坐标;若不存在,请说明理由.