湖北省黄冈、孝感、咸宁市2023年中考数学试卷
试卷更新日期:2023-07-17 类型:中考真卷
一、单选题
-
1. 的相反数是 ( )A、 B、 C、 D、2. 2023年全国普通高校毕业生规模预计达到1158万人,数11580000用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体中,三视图都是圆的是( )A、长方体 B、图柱 C、圆锥 D、球4. 不等式的解集为( )A、 B、 C、 D、无解5. 如图,的直角顶点A在直线a上,斜边在直线b上,若 , 则( )
 A、 B、 C、 D、6. 如图,在中,直径与弦相交于点P,连接 , 若 , , 则( )
A、 B、 C、 D、6. 如图,在中,直径与弦相交于点P,连接 , 若 , , 则( ) A、 B、 C、 D、7. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )
A、 B、 C、 D、7. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )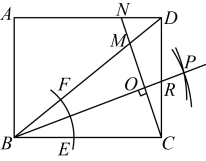 A、 B、 C、 D、48. 已知二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列论中:①;②若点均在该二次函数图象上,则;③若m为任意实数,则;④方程的两实数根为 , 且 , 则 . 正确结论的序号为( )A、①②③ B、①③④ C、②③④ D、①④
A、 B、 C、 D、48. 已知二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列论中:①;②若点均在该二次函数图象上,则;③若m为任意实数,则;④方程的两实数根为 , 且 , 则 . 正确结论的序号为( )A、①②③ B、①③④ C、②③④ D、①④二、填空题
-
9. 计算; .10. 请写出一个正整数m的值使得是整数; .11. 若正n边形的一个外角为 , 则 .12. 已知一元二次方程的两个实数根为 , 若 , 则实数 .13. 眼睛是心灵的窗户为保护学生视力,启航中学每学期给学生检查视力,下表是该校某班39名学生右眼视力的检查结果,这组视力数据中,中位数是 .
视力
4.0
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
50
人数
1
2
6
3
3
4
1
2
5
7
5
14. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号) 15. 如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中 , , 连接 , 若与的面积相等,则 .
15. 如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中 , , 连接 , 若与的面积相等,则 . 16. 如图,已知点 , 点B在y轴正半轴上,将线段绕点A顺时针旋转到线段 , 若点C的坐标为 , 则 .
16. 如图,已知点 , 点B在y轴正半轴上,将线段绕点A顺时针旋转到线段 , 若点C的坐标为 , 则 .
三、解答题
-
17. 化简: .18. 创建文明城市,构建美好家园.为提高垃圾分类意识,幸福社区决定采购A,B两种型号的新型垃圾桶.若购买3个A型垃圾桶和4个B型垃圾桶共需要580元,购买6个A型垃圾桶和5个B型垃圾桶共需要860元.(1)、求两种型号垃圾桶的单价;(2)、若需购买A,B两种型号的垃圾桶共200个,总费用不超过15000元,至少需购买A型垃圾桶多少个?19. 打造书香文化,培养阅读习惯,崇德中学计划在各班建图书角,开展“我最喜欢阅读的书篇”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:科技类,B:文学类,C:政史类,D:艺术类,E:其他类).张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).

根据图中信息,请回答下列问题;
(1)、条形图中的 , , 文学类书籍对应扇形圆心角等于度;(2)、若该校有2000名学生,请你估计最喜欢阅读政史类书籍的学生人数;(3)、甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.20. 如图,中,以为直径的交于点 , 是的切线,且 , 垂足为 , 延长交于点 . (1)、求证:;(2)、若 , 求的长.21. 如图,一次函数与函数为的图象交于两点.
(1)、求证:;(2)、若 , 求的长.21. 如图,一次函数与函数为的图象交于两点. (1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.22. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .
(1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.22. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .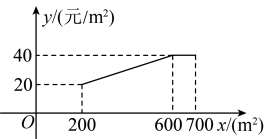 (1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?23. 【问题呈现】
(1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?23. 【问题呈现】和都是直角三角形, , 连接 , , 探究 , 的位置关系.
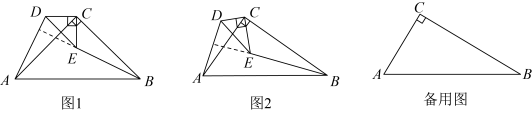 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
24. 已知抛物线与x轴交于两点,与y轴交于点 , 点P为第一象限抛物线上的点,连接 .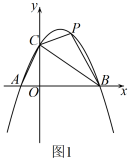
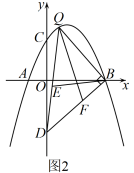
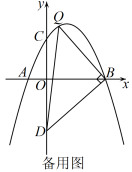 (1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.
(1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.①求m的值;
②设的面积为S,若 , 请直接写出k的取值范围.